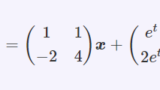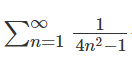【神戸大学】工学研究科 電気電子工学専攻 院試対策(数学)

数学の試験範囲

線形代数、解析学、微分方程式、複素関数、フーリエ変換(ラプラス変換)からなります。

複素関数は、フーリエ変換と一緒に出題されることがありますが、4題に分けて基本的に全分野出題されます。満遍なくの対策が必要です。

神戸大 電気電子工学専攻 院試の全体

少し、トリッキーな入試方式になっています。というのも、同じ専攻の中でも受ける研究室によって選択する科目が変わります。

研究室問わず、数学、電気回路、電子回路は必須選択です。

しかし、残りの科目は下記のような選択ルールになっています。

平たく言えば、電子系の研究室を志望するか、情報系の研究室を志望するかで選択科目が変わるようです。

両方の分野で選択できる科目は無いため、早めに志望研究室について固めておく必要があると思います。

数学について、解き進めることはできるが、完答するには少し難しいと思います。

というのも、4分野全て解答する必要があり、それぞれの分野は幅広く問われるからです。

極値の計算は、工夫してやらないとドツボにはまる年がありますし、複素関数も、ただ積分するだけでなく、帰納法から結果を類推する問題が出たりします。

このように、市販の問題集では見ないような問題が毎年1問くらい含まれているため、少し難しいと考えています。

落ち着いて考えればいつかは解ける難易度ですが、これを院試本番の90分で行うには厳しいと思います。

7,8割取っておいて、次の電気回路、電子回路、選択科目にパスすることが最適でしょう。

全体

最近3年分は以下の分野の出題がありました。

バリエーションが多いですが、分野別に見ていきます。

解析学：冒頭で説明した通り、2変数関数の極値を求める問題が多いです。年度ごとに問われ方が変わりますが、\(f_{x}=f_{y}=0\)を評価する原則は、共通で守っていきたい。

線形代数：行列の対角化と成分計算で済むことが多いので、是非得点したいです。

微分方程式：個人的には、神戸大数学のセットの中では難しい方と思います。変数変換を行う誘導は付いているものの、そこから係数が定数になるまで微分方程式を変換する作業は対策必須です。ロンスキアンの計算も頻出で、総じて計算量も多いです。部分点でも仕方ないかもしれません。

複素関数：九大と似ていて、ある積分路内の孤立特異点の留数を取る問題が多いです。ジョルダンの補助定理を用いて広義積分の値を求める問題はあまり出ません。留数定理を忠実に使っていきましょう。

フーリエ変換、ラプラス変換：\(\exp(-t)\sin(t),exp(-t)\cos(t)\)など、減衰曲線の問題が多いです。cosは偶関数、sinは奇関数である性質を利用し、計算量を少なくして解いていくと良いです。

・対策に役立ちそうな本サイトの記事 (是非ご覧ください)

教科書(解析学)

一般教養科目のため、統一した教科書が無いです。他の大学にも言えることですが、自身のお持ちの教科書で問題無いと思います。ここでは、問題集だけ紹介します。

解析演習 (数学演習ライブラリ 2) 野本 久夫 (著), 岸 正倫 (著)

極値の問題をやりこむ方と良いと思います。これまでの傾向から、他大学だと頻出の重積分は控えめで良いと考えます。

線形代数

成分計算で済む問題が多いことから、個別に問題集を買っての対策は基本不要と考えます。

他大学の対策も視野に入れて買うとなると、下記が定番の問題集になります。

演習 線形代数 寺田 文行 (著)

微分方程式

ここからが、神戸大のシラバス上専門科目になっているようです。下記がシラバスで紹介されている本になります。

微分方程式入門，南部隆夫著 (シラバス対象本)

「常微分方程式演習」という講義にて紹介されています。演習専門の講義があることから、神戸大の熱の入りようが伺えます。

最近出版された本であることから、見やすいレイアウトになっています。まだ、微分方程式の本をお持ちではない時は、買っても良いかもしれません。

演習微分方程式 (演習数学ライブラリ 新版 3) 寺田 文行 (著), 坂田 ひろし (著)

微分方程式の対策問題集の定番です。他大学の院試においてもオススメしています。

変数変換の問題は少ないですが、それでも様々な型の練習ができることから、是非選択したいです。

複素関数、フーリエ変換

これも専門科目です。シラバスに載っている本を紹介していきます。

演習応用解析　洲之内 治男 (著) (シラバス対象本)

演習量としては豊富ですが、神戸大院試の対策としては微妙です。(個人的な見解ですが)

というのも、神戸大の複素関数の頻出分野である孤立特異点の留数定理の問題が豊富に含まれているわけでもなく、特殊関数やベクトル解析など、院試範囲外の項目も記載されているからです。

他にもシラバスで紹介されている本はあります。ただ、数学という学問を修めることに適してはいますが、院試をクリアするという意味ではこれも微妙かもしれません。

解析概論　高木 貞治 (著)

管理人としては、分かりやすさの観点から下記の本をオススメします。フーリエ変換、ラプラス変換の内容もあって、1冊である程度のレベルまで対策可能です。

応用数学 (工学系数学テキストシリーズ)工学系数学教材研究会(編集)/上野健爾(監修) (著)

ラプラス変換

シラバスを確認していましたが、対象となる講義を見つけることが出来ませんでした。

2023年度の入試で初めての出題であり、内容としても初歩的な問題であったことから、ご自身の教科書で勉強すると良いです。

強いて言えば、上記複素関数の章で私が紹介した参考書を使用すると良いです。

対策に使える他大学の問題

少し独特な問題もあるので、全てオススメできるわけではないです。実際に確認し、使えると判断した問題を演習すると良いです。

解析学は、極値を判定する問題が多い大学を赤字にしました。神戸大の傾向と似ていると思います。

線形代数は、成分計算を行う問題が多い大学を赤字にしました。北大が、レベル、分量ともに合っていると思います。

微分方程式：変数変換を用いる問題が多い大学を赤字にしました。北大、広島大が毎年のように出題されるため、参考になると思います。

複素関数、フーリエ変換、ラプラス変換は、出題する大学のリストアップはしたものの、オススメできる大学はありません。ここは、神戸大色が出る問題が多いと思います。

孤立特異点を用いた複素積分　→　大阪公立大
帰納法などで、計算結果を推定する　→阪大

が、少しは参考になるかもしれません。

問題集の完成度を上げていった方が良いと思います。

最後に

神戸大院試の数学は、範囲が広いため、対策に時間がかかります。

是非、今の内から幅広く対策を進め、本番の得点源にしましょう。