ラグランジアンを用いた電気-機械エネルギー変換

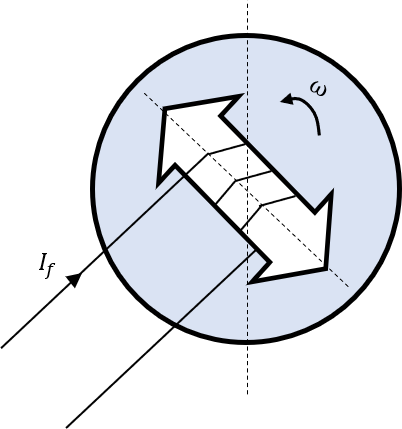
下図の回転型蓄電器を考える。角度が0度のとき、静電容量100μF、角度が180度のとき、500μFとする。静電容量は角度に対して直線的に変化する。この蓄電器の両端に1000Vの電圧をかけたとき、回転子に働くトルクの大きさを求めよ。

ただし、電気回路上の抵抗Rと機械駆動系の粘性抵抗rの影響は無視する。また、電気回路上のインダクタンス成分Lは無視し、回転速度は一定値とする。

可変型蓄電池
機械電気工学Ⅱ 第7章演習問題(2)から数値を変更。細かい条件(第2文目ただし～)を追記

はじめに
ラグランジュの運動方程式
解答例
最後に
参考文献

はじめに

こちらの問題、電験などの実学勉強中心だと面食らうかもしれません。(単に試験範囲に入っていないだけかもしれませんが。。。)

電圧が与えられていることで、\(P=VIcos\theta=\omega T\)の関係式を使用し、トルクを求められないかまず考えると思います。しかし、問題文には電圧以外の条件が与えられていません。よって、この方法を使用して解くことは難しいです。

このようなとき、ラグランジアンLを使用すると解決します。解析力学の知識が無い場合は、運動エネルギーに位置エネルギーを引いたものと捉えていただいて構いません。

今回は、電気回路としてのラグランジアンを求めることになります。これをラグランジュの運動方程式に代入することで、トルクを求めることができます。

ラグランジュの運動方程式

ラグランジアンをL、消散関数をFとすると、機械系、電気系それぞれ次式で表されます。

機械系の場合

\begin{eqnarray}f=\dfrac{d}{dt}\left( \dfrac{\partial L}{\partial v}\right) -\dfrac{\partial L}{\partial x}+\dfrac{\partial F}{\partial v}\end{eqnarray}

運動エネルギーTは、高校物理と同じく\(T=\dfrac{1}{2}mv^{2}\)になります。

位置エネルギーUも同様に、ばね定数sを用いて\(U=\dfrac{1}{2}sx^{2}\)になります。

消散関数Fは、エネルギー損失を表しています。

粘性抵抗\(rv\)を\(v\)で積分し、\(F=\dfrac{1}{2}rv^{2}\)で表されます。

左辺 f は力を表します。xは位置(座標)で円筒座標の場合は\(\theta\)になります。

このとき、fはトルクTに該当するので、本問を解くヒントになりそうです。

電気系の場合

位置x→電荷q、速度v→電流i、加速度\(\dfrac{dv}{dt}=\dfrac{di}{dt}\)とする。

以下のようにあらわされます。

\begin{eqnarray}e=\dfrac{d}{dt}\left( \dfrac{\partial L}{\partial i}\right) -\dfrac{\partial L}{\partial q}+\dfrac{\partial F}{\partial i}\end{eqnarray}

運動エネルギーTは、コイルによる磁気エネルギーに相当する。インダクタンスをLとすると、\(T=\dfrac{1}{2}Li^{2}\)で表されます。

位置エネルギーUは、コンデンサによる静電エネルギーに相当する。静電容量をCとすると、\(U=\dfrac{1}{2C}q^{2}\)で表されます。

ここで、消散関数Fを考えます。抵抗値によるジュール損失\(Ri^{2}\)に1/2をかけると、機械系と同じ形になります。\(F=\dfrac{1}{2}Ri^{2}\)になります。

解答例

解答の方針

前章の対応関係を用いれば、機械系と電気系のラグランジュの運動方程式は等価に扱ってよいです。

問題文では、電気回路パラメータを与えられているので、こちらを用いてラグランジアンLを求める。

その結果を機械領域の運動方程式に代入することで、トルクを求めることができそうと考えられます。(問題文で設定されている条件は回転子なので、円筒座標です。機械系の運動方程式の左辺はトルクTになります。)

解答内容

問題文の条件から、静電容量は\(\theta\)を変数に取ると以下で表すことができる。

\begin{eqnarray}C(\theta)=100+400\dfrac{\theta}{\pi} [μF]\end{eqnarray}

コイル成分は考えないため、電気系の運動エネルギー\(T=0\)

電気系の位置エネルギー\(U=\dfrac{q^{2}}{2C(\theta)}\)で表されるので、

ラグランジアンLは、\(L=-U=-\dfrac{q^{2}}{2C(\theta)}\)になる。

これを機械系のラグランジュの運動方程式(1)に代入する。

今回は、回転座標系のため、位置 \(x →\theta\)に変換して考える。

角速度は一定のため、右辺の第1項は0。粘性抵抗も無いため、第3項は0。

よって、求めるトルクTは以下の式で書ける。

\begin{eqnarray} |T|&=&\left|-\dfrac{\partial L}{\partial \theta} \right|\\ &=& \left|\dfrac{1}{2} \dfrac{\partial }{\partial \theta} \left( \dfrac{1}{C(\theta)} \right) q^{2} \right| \\ &=& \left|\dfrac{1}{2} \dfrac{\partial C(\theta)}{\partial \theta} \dfrac{\partial }{\partial C(\theta)} \left( \dfrac{1}{C(\theta)} \right)q^{2} \right|\\ &=& \left|\dfrac{1}{2} \dfrac{\partial C(\theta)}{\partial \theta} \left(-\dfrac{q^2}{C(\theta)^{2}}\right) \right| \\ &=& \dfrac{1}{2} 10^{-6} \dfrac{400}{\pi}(1000)^{2} \\ &=& \dfrac{200}{\pi} \end{eqnarray}

なお、\(q=C(\theta)V\)で、\(V=1000\)より、\(\dfrac{q}{C(\theta)}=1000[N・m]\)である。