変圧器の等価回路と発生する損失、最大効率を例題で解説

[問題1]
ある単相変圧器について、無負荷試験により、励磁アドミタンスとして$G-jB$を、短絡試験により、1次側に換算した合計巻き線抵抗及び合計漏れリアクタンスとして$R+jX$をそれぞれ得た。
GおよびRによって変圧器で損失が発生する。それぞれの損失の特徴を簡単に説明しなさい。

神戸大学大学院 電気電子工学専攻 電力工学 2019より抜粋 一部改変

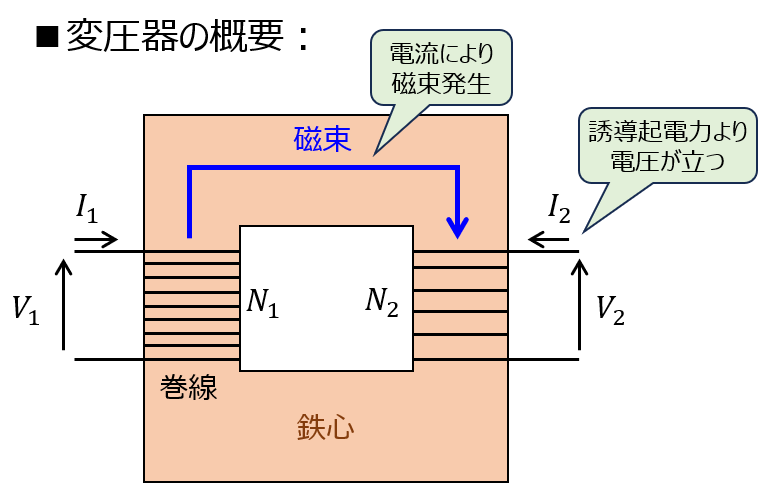
変圧器について

電圧を変換するための機器です。

電柱の上にバケツのような物体があることを目にしたことがあるかもしれません。あれは小型変圧器です。電線に流れている電気を家屋内に供給するため、電圧をより低圧に変換しています。

変圧器の構成として、磁束を流すための鉄心があり、その左右に銅線を巻いた構成になっています。

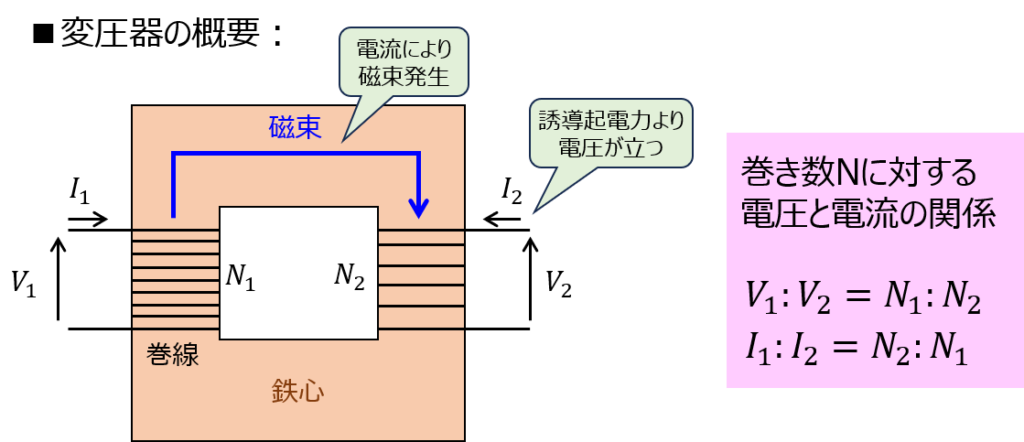
銅線の巻き数比により、左(一次側)から入って来た電圧を右(二次側)に変換します。

1次側と2次側の電圧比は、巻き数比に対応します。

例)1次側と2次側の巻き数が１：２のとき、電圧は1次側：200V、2次側：400V。など

変圧器の誘導起電力(実効値)

今、変圧器の一次側に$V=V_m\sin (2\pi ft)$なる正弦波を流したとします。

鉄心の面積を$S$、一次側の巻き数を$N_1$とすると、誘導起電力$e$は

$$\begin{array}{}\text{(1)}& \begin{array}{r}e=N_1{\displaystyle \frac{d\varphi }{dt}}=2\pi f{V}_{m}S{N}_1\cos 2\pi ft\end{array}\end{array}$$

となり、最大値は$e_{max}=2\pi f{V}_{M}S{N}_1$となります。

実効値$\bar{e}$は、最大値に対し$\frac{1}{\sqrt{2}}$倍すれば良いので

$$\begin{array}{}\text{(2)}& \begin{array}{r}\bar{e}={\displaystyle \frac{2\pi f{V}_{M}S{N}_1}{\sqrt{2}}}=4.44f{N}_1{V}_{m}S\end{array}\end{array}$$

となります。この「4.44」という数値はよく試験で出てきます。丸暗記でも良いですが、比較的楽に導出できます。結果、導出ともに覚えておきましょう。

なお、誘導起電力は周波数、巻き数の1乗に比例します。こちらもたまに問われます。

変圧器の等価回路

下記で表すことができます。

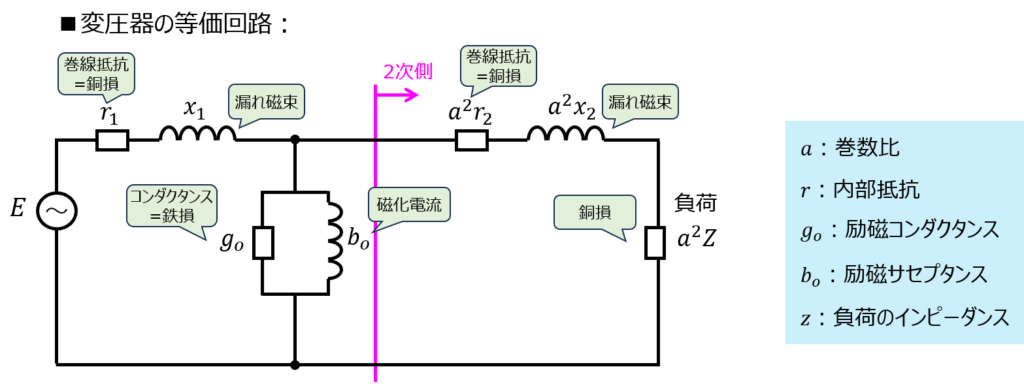
$r_1$は、一次側の巻線抵抗、$x_1$は一次側の漏れリアクタンスです。$r_2$など、添え字に2が付く場合は二次側のパラメータに読み替えてください。$g_o$は励磁コンダクタンス、$b_o$は励磁サセプタンス、$a$は一次側と二次側の巻き線比を表します。

変圧するときに発生する物理現象を正しく理解できれば、それぞれのパラメータが必要な意味も把握できます。

下記に示していきます。

巻線抵抗$r$ について

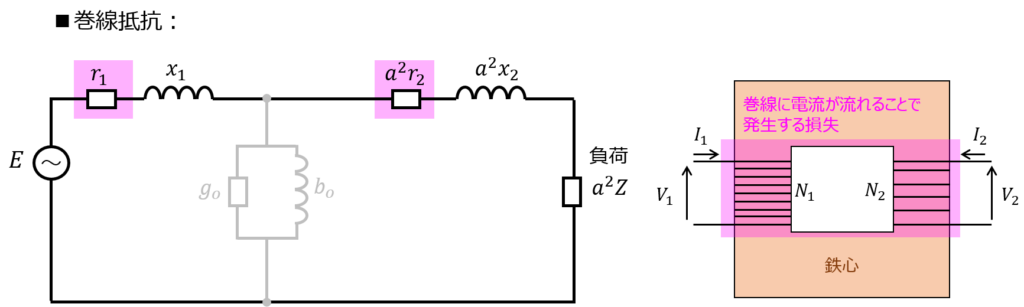
これは単純で、電流を流した時に発生するオームの法則によるものです。

電圧が立ち、ジュール損が発生することから、このパラメータが必要です。

漏れリアクタンス$x$について

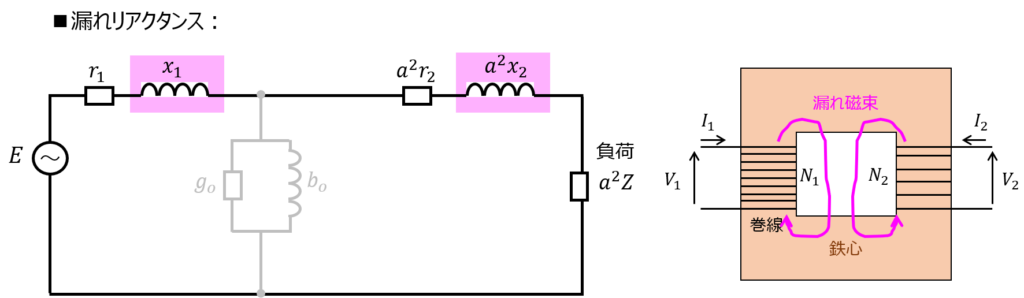
鉄心内を磁束が流れる時、現実では全てが2次側に到達するわけではありません。

一部は大気中に漏れ出て、一次側の巻き線コイルに対しループ磁場を発生します。

これを表現したものが漏れリアクタンスになります。

励磁コンダクタンス$g_o$、励磁サセプタンス$b_o$について

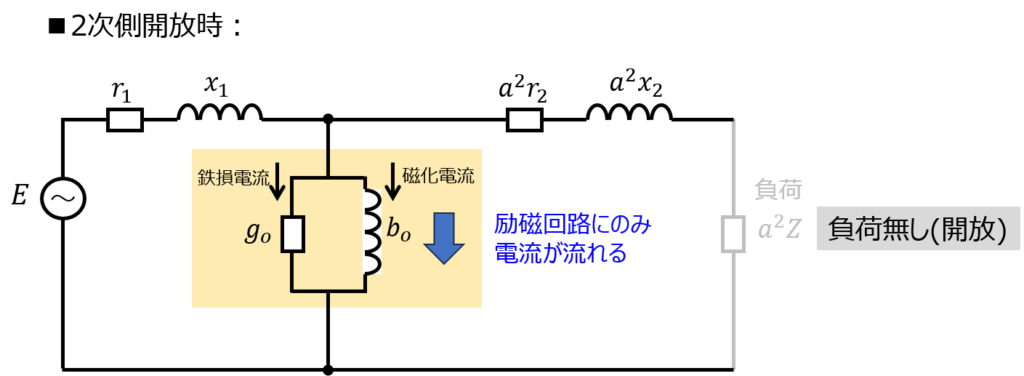
2次側を無負荷(開放)にしたとき、1次側に電圧を加えた時に流れる励磁電流を回路パラメータとして表現したものになります。

先の等価回路的に、2次側を開放したとき、2次側に電流は流れません。

1次側で回路を形成する必要があり、そのためのパラメータになります。

$g_o$を流れる電流は鉄損電流と言います。抵抗のため、ジュール損として発生する損失です。変圧器として固定値で発生し、2次側に負荷を接続したときも発生します。

$b_o$を流れる電流は磁化電流と言います。変圧器内に磁束を発生させるために必要な電流です。

なお、$g_o,b_o$を合成したパラメータを、励磁アドミタンス$Y_o$と言います。問題ではこちらの呼ばれ方をするときがあります。同じく覚えておきましょう。

電源の周波数を大きくしたとき

コイルのリアクタンスは$j\omega L$で表されます。よって、電源周波数を大きくしたときは$\omega$が大きくなるため、励磁回路のリアクタンスが増加します。

このようにして、励磁電流は減少します。(なんとなく、誘導起電力が大きくなるから励磁電流が大きくなりそうだと考えがちですが、前節の回路から、そのようなことはありません。注意しましょう。)

変圧器の損失

前章の等価回路で考えると分かりやすいですが、鉄損と銅損の2種類存在します。

鉄損

先の説明の通り。変圧器として発生する損失です。(固定値)

無負荷のときでも発生することから、無負荷損と呼ばれることもあります。

鉄損は、ヒステリシス損失と渦電流損失に分けられます。

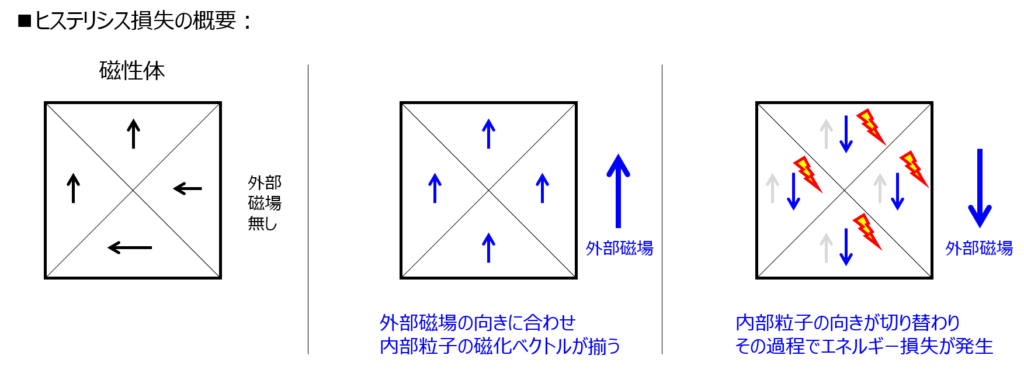
ヒステリシス損失

磁性体内部の磁区の移動により発生する損失です。

磁場を印可したとき、磁場の方向に沿うように磁区の向きが変化します。

磁場の方向が変わるとき、再び磁区も変化します。

このとき、磁区内部では、内部粒子の向きが変わることによるエネルギー損失が発生します。

これをヒステリシス損失と言います。周波数の1乗に比例します。

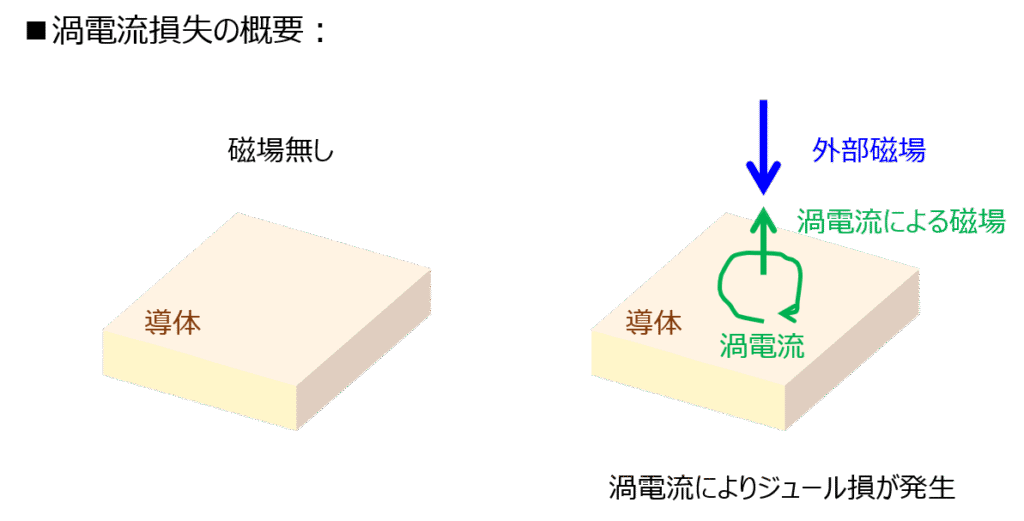
渦電流損失

外部磁場の変化による誘導起電力が発生し、渦状の電流が流れることにより発生する損失です。

IHヒーターとして使用する用途もありますが、変圧器として使う分には損失になります。

周波数の2乗に比例します。

銅損

一次側と二次側の巻線抵抗、負荷に電流が流れることによるジュール損失です。

ジュール熱の式$P=r{I}^2$より、電流の2乗に比例します。

変圧器の最大効率

負荷比$a$を

$$\begin{array}{}\text{(3)}& \begin{array}{r}a={\displaystyle \frac{\mathrm{現}\mathrm{在}\mathrm{の}\mathrm{負}\mathrm{荷}\mathrm{容}\mathrm{量}}{\mathrm{定}\mathrm{格}\mathrm{容}\mathrm{量}}}\end{array}\end{array}$$

と定義し、現在の負荷容量を$P$、鉄損を$P_i$、銅損を$P_c$、変圧器の効率$\eta$は下記になります。

$$\begin{array}{}\text{(4)}& \begin{array}{r}\eta ={\displaystyle \frac{P\cos \theta }{P\cos \theta +\frac{P_i}{a}+a{P}_c}}\end{array}\end{array}$$

分母が最小になるとき、最大効率になります。

負荷容量$P$は一定値とし、鉄損と銅損の関係に注目します。

相加相乗平均の関係より、鉄損=銅損になるとき、分母は最小になります。

よって、$\frac{P_1}{a}=a{P}_c$のとき効率最大になります。

また、負荷比の概念を除き、単純に入力と出力の比を取った場合を規約効率と言い、下記の式で表されます。

$$\begin{array}{}\text{(5)}& \begin{array}{r}\eta ={\displaystyle \frac{P\cos \theta }{P\cos \theta +P_i+P_c}}\end{array}\end{array}$$

分母は鉄損や銅損の損失分を考慮するに対し、分子は出力分だけ考慮するので上記関係式になっています。

解答例

前置きが長くなりましたが、解答は下記になります。

問題1 G、Rに関わる損失

G：鉄損に相当し、ヒステリシス損、渦電流損を回路パラメータとして表している。

R：銅損に相当し、Rに流れる電流の2乗に比例して増加する。

問題2 変圧器の鉄損、銅損、最大効率の計算問題

(1)鉄損の計算

(5)式を用いて解いていきます。

鉄損を$P_i$、出力が2[kW]のときの銅損を$P_c$とする。この時の2次側(100[V])の電流値は$20[A]$に対し、出力が8[kW]のときの電流値は80[A]。ジュール熱より、銅損は電流の2乗に比例する。よって、出力が8[kW]のときの銅損は$16P_c$となる。

効率の式により、下記の関係式が導かれる。

$$\begin{array}{}\text{(6)}& \begin{array}{r}{\displaystyle \frac{2}{2+P_i+P_c}}={\displaystyle \frac{8}{8+P_i+16P_c}}=0.96\end{array}\end{array}$$

これを解いて、$P_i=0.063[kW],P_c=0.017[kW]$

(2)最大効率のときの出力

鉄損と銅損が等しくなる時、最大効率となる。

変圧器の巻き線抵抗を$r$とすると、(1)より、電流20Aのときに銅損17W。ジュール熱の関係により

$$\begin{array}{}\text{(7)}& \begin{array}{r}r\ast 400=17\end{array}\end{array}$$

$r=\frac{17}{400}$が得られる。鉄損と等しくなる時の電流$I$は

$$\begin{array}{}\text{(8)}& \begin{array}{r}{\displaystyle \frac{17}{400}}\ast I^2=63\end{array}\end{array}$$

$$\begin{array}{}\text{(9)}& \begin{array}{rl}I& =\sqrt{{\displaystyle \frac{63}{17}}}\ast 20\end{array}\end{array}$$

$$\begin{array}{}\text{(10)}& \begin{array}{r}I=38.5[A]\end{array}\end{array}$$

以上より、求める出力$P=VI$は、

$$\begin{array}{}\text{(11)}& \begin{array}{r}P=VI=100\ast 38.5=3850[W]\end{array}\end{array}$$

最大効率は

$$\begin{array}{}\text{(12)}& \begin{array}{rl}{\eta }_{max}& ={\displaystyle \frac{3850}{3850+63\ast 2}}\\ & =0.968\end{array}\end{array}$$

最後に

変圧器は、将来電力関係の仕事についたとき、必ず密接に関わる電気機器になります。

他、電気主任技術者試験でも毎年必ず出題されます。

院試の先に、本分野の就職を志す方は、最優先で覚えましょう。