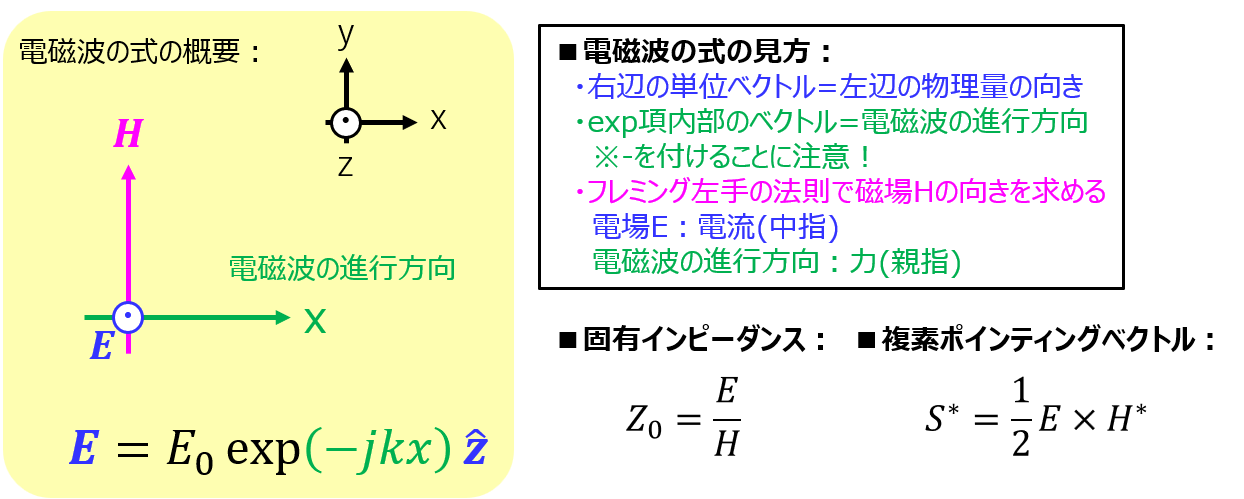
直交座標系にて、以下の式の電磁波(電場成分)が真空中\((\varepsilon_{0}, \mu_{0})\) を伝搬する。
\begin{eqnarray}\boldsymbol{E}=E_{0}\exp \left( -j\left( k x-\omega t\right) \right) \widehat{\boldsymbol{z}}\end{eqnarray}
(1)電磁波の進行方向、電場\(\boldsymbol{E}\)の方向、磁場\(\boldsymbol{H}\)の方向を示せ。
(2)磁場\(\boldsymbol{H}\)を問題文で記載した文字で表せ。また、真空中の固有インピーダンス\(Z_{0}\)を求めよ。
(3)ポインティングベクトルの時間平均値を求め、物理的意味について説明せよ。
電磁波とは
時間変動する場において、電場と磁場は時間微分項を通して結びつき、互いを源として発生する波になります。
以下のマクスウェル方程式から生まれた概念です。
\begin{cases}rot\boldsymbol{E}=-\dfrac{\partial \boldsymbol{B}}{\partial t}\\ rot\boldsymbol{H}=\boldsymbol{i}+\dfrac{\partial \boldsymbol{D}}{\partial t}\end{cases}
1式目が電磁誘導の法則、2式目がアンペールマクスウェルの法則を表しています。
右辺に磁束密度、電束密度がそれぞれ存在します。それぞれ時間微分項を通して結びついています。時間変動することが前提ならば、両者は互いに影響し、電磁波の性質があると考えられます。
電磁波の性質
- 電場、磁場と進行方向は垂直に交わる
- 電場と磁場は同位相
- 電磁場の角周波数、波数、速度の関係は、\(\omega=ck\)で表される。
証明
z方向に伝搬する電磁場の電場成分
\begin{cases}\boldsymbol{E}=(E_{x},0,0) \\ E_{x}=E_{o}\sin(kz- \omega t)\end{cases}
について、マクスウェル方程式
\begin{aligned}rot(\boldsymbol{E})=-\dfrac{\partial \boldsymbol{B}}{\partial t}\end{aligned}を用いて
\begin{aligned}rot(\boldsymbol{E})=\left(0,\frac{\partial E_{x}}{\partial z},0 \right)\end{aligned}
\begin{aligned}\frac{\partial E_{x}}{\partial z}=kE_{o}\cos(kz- \omega t)\end{aligned}
を積分し
\begin{aligned}B_{y}=\dfrac{kE_{o}}{\omega}\sin(kz-\omega t)\end{aligned}
(3)式、(7)式より、電場と磁場はそれぞれx成分、y成分のみを持ち、直交する。
また、\(E_{x}=E_{o}\sin \lbrace k(z- \frac{\omega}{k} t)\rbrace \)と式変形でき、カッコ内の第2項が時間項(伝搬速度)を表しているので
\begin{aligned}c= \frac{\omega}{k} \Leftrightarrow \omega=ck\end{aligned}
が成立する。
解答方針
- exp項の内部が電磁波の進行方向を示す。
- フレミング左手の法則を活用し、与えられていない物理量(電場/磁場)ベクトルの向きを決定する。
- マクスウェル方程式を利用し、電場/磁場の式を求める
- 固有インピーダンスは、電場\(E\)と\(H\)の絶対値\(Z_{0}=\dfrac{E}{H}\)で与えられる。
- 複素ポインティングベクトル\(\boldsymbol{S^{\ast }}=\dfrac{1}{2}\boldsymbol{E}\times \boldsymbol{H^{\ast }}\)を利用すると、時間平均値を簡単に求められる。
<図解>
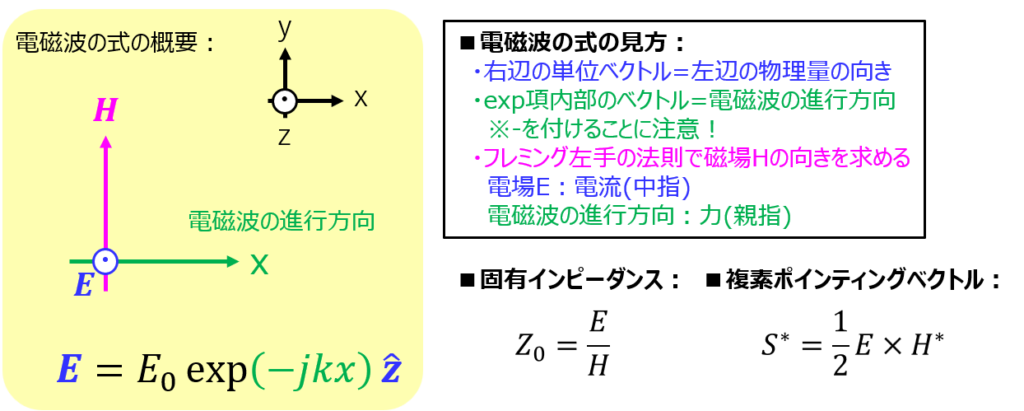
透過、反射に関する問題も出てきますが、基本的にマクスウェル方程式を解くことで解決するパターンが多いです。(先の証明でも使いました。)
- 電場(E)が未知数の場合、式(2)の第1式に磁場Hを代入し、計算する。
- 磁場(H)が未知数の場合、式(2)の第2式に電場Eを代入し、計算する。
上記の計算は、電磁波の問題が出題されたとき、必ずと言って良いほど使用します。本問を通して是非マスターしてください。
複素ポインティングベクトルに関する考え方
ポインティングベクトルの時間平均値を考えるとき、E,Hの一方に共役複素数を取り、複素ポインティングベクトルを利用すると簡単に求められます。
まず、共役を取らずに普通に計算してみます。
\begin{eqnarray}\overline{p}=\dfrac{1}{T}\int _{0}^{T} E_{0}H_{0}\exp(-2j(kx-\omega t))\end{eqnarray}
exp項の実部を取り、\begin{aligned}(9)&=\dfrac{1}{T}\int _{0}^{T}E_{0}H_{0}\cos ^{2}(-2j\left( kx-\omega t\right)) \\ &=\dfrac{E_{0}H_{0}}{2} \end{aligned}
cos項は倍角の公式を利用します。途中の計算を省略しましたが、中々面倒です。試験中にするのはなかなかのリスクです。
そんなとき、複素ポインティングベクトル\(\boldsymbol{S^{\ast }}=\dfrac{1}{2}\boldsymbol{E}\times \boldsymbol{H^{\ast }}\)を用いれば楽に求めることができます。
上式のように、時間平均値を求めるとき、結局実部しか考えないため
- 共役複素数を取りexp項を予め消去しておく。
- 実効値の考え方から、時間平均値は振幅に対し\(\dfrac{1}{\sqrt{2}}*\dfrac{1}{\sqrt{2}}=\dfrac{1}{2}\)倍される。
この影響を予め式に反映しておくと楽に計算できます。それが、複素ポインティングベクトルです。\(\dfrac{1}{\sqrt{2}}\)を2回かけている理由は、\(\boldsymbol{E}\)と\(\boldsymbol{H}\) 2つの実効値をそれぞれ考えるためです。)
ポインティングベクトルの向きは、電磁波の進行方向と一致します。
補足1
教授によっては、複素ポインティングベクトルを\(\boldsymbol{S^{\ast }}=\boldsymbol{E}\times \boldsymbol{H^{\ast }}\)と、\(\dfrac{1}{2}\)が無い場合で教えられることもあります。これは、時間平均値を振幅平均で取るか、振幅の最大で取るかの違いです。
後者の場合は、\(\dfrac{1}{2}\)倍されずに、\(\boldsymbol{E}\)と\(\boldsymbol{H^{\ast}}\)の外積を取ったものがそのまま答えになります。
補足2
作問者によってはexp項内部の\(\omega t\)を省略し、下記のように表すことがあります。
\begin{eqnarray}\boldsymbol{E}=E_{0}\exp \left( -j k x \right) \widehat{\boldsymbol{z}}\end{eqnarray}
このような表記でも、\(\omega t\)項は存在します。時間微分するとき、上記の式を信用して計算ミスすることが無いようにしましょう。
補足3
電磁波は反時計回りです。そのため、一般的に、exp項の乗数が負であることを正の向きとします。本問は、\(\exp(-jkx)\)ですので、+x方向に伝搬すると考えます。
仮に、時計回りと仮定する場合は、exp項の乗数が正であることを正の向きとします。このとき、本問の場合は、-x方向になります。
電信方程式と波動方程式
式(2)の両辺に回転(rot)を取って計算すると、以下の式を導くことができます。
\begin{cases}\Delta \boldsymbol{E}-\varepsilon_{0} \mu_{0} \dfrac{\partial ^{2}\boldsymbol{E}}{dt^{2}}- \sigma \mu_{0} \dfrac{\partial \boldsymbol{E}}{\partial t}=0\\ \Delta \boldsymbol{H}-\varepsilon_{0} \mu_{0} \dfrac{\partial ^{2}\boldsymbol{H}}{\partial t^{2}}-\sigma\mu_{0} \dfrac{\partial \boldsymbol{H}}{\partial t}=0\end{cases}
これを電信方程式と言い、分布定数回路の問題を考えるうえで基本となる式になります。(導出については他サイト様でも説明されているため、割愛します。)
絶縁媒質のとき、\(\sigma=0\)になるため、下記の式になります。
\begin{cases}\Delta \boldsymbol{E}-\varepsilon_{0} \mu_{0} \dfrac{\partial ^{2}\boldsymbol{E}}{dt^{2}}=0\\ \Delta \boldsymbol{H}-\varepsilon_{0} \mu_{0} \dfrac{\partial ^{2}\boldsymbol{H}}{\partial t^{2}}=0\end{cases}
これを波動方程式と言います。本問では、こちらを利用します。
第1項のラプラシアン\(∆\)で勾配を取り、第2項で時間微分を2回行った結果が等しいことを見るに、電場、磁場は時間(t)と位置(x,y,z)を変数に取ることが分かります。
ですので、式(1)のように表すことができます。
東北大院では導出自体を出題されることがあります。本大学を志望する方は、是非対策しましょう。
解答例
(1)波の伝搬方向
電磁波の伝搬方向:式(1)のexp項に注目すると、xの符号がある。電磁波が反時計周りの場合は-x方向になる。
電場の方向:式(1)より、明らかに+z方向
磁場の方向:フレミング左手の法則により、+y方向
(2)磁場の式
真空は絶縁媒質であることから、\(\sigma=0\)。
アンペール・マクスウェルの法則を利用し、下記のように計算する。(1)より、磁場はy成分\(H_{y}\)しか存在しないので
\begin{aligned}rot\boldsymbol{H}&=\dfrac{\partial \boldsymbol{D}}{\partial t}\end{aligned} に、各成分を代入し、\begin{aligned} \begin{vmatrix} \widehat{\boldsymbol{x}} & \widehat{\boldsymbol{y}} & \widehat{\boldsymbol{z}} \\ \dfrac{\partial }{\partial x} & \dfrac{\partial }{\partial y} & \dfrac{\partial }{\partial z} \\ Hx & Hy & Hz \end{vmatrix}&=-\varepsilon _{0}j\omega E_{0}\exp(-j\left( k x-\omega t\right))\widehat{\boldsymbol{z}} \\ \dfrac{\partial Hy}{dx}&=-j\omega \varepsilon _{0}\omega E_{0}\exp(-j\left( k x-\omega t\right)) \\ H_{y}&=\dfrac{\varepsilon _{0}\omega }{k}E_{0}\exp(-j\left( k x-\omega t\right)) \\ &=\sqrt{\dfrac{\varepsilon_{0} }{\mu _{0}}}E_{0}\exp(-j\left( k x-\omega t\right))\end{aligned}
なお、\(k=\omega \sqrt{\varepsilon _{0}\mu _{0}}\)の関係を用いた。
以上より、求める固有インピーダンスは
\begin{eqnarray}Z_{0}=\dfrac{E_{z}}{H_{y}}=\sqrt{\dfrac{\mu _{0}}{\varepsilon _{0}}}\end{eqnarray}
(3)ポインティングベクトルの時間平均値
複素ポインティングベクトルを取り
\begin{aligned}S^{\ast }&=\dfrac{1}{2}E_{0}\exp(-j\left( k x-\omega t\right)) E_{0}\sqrt{\dfrac{\varepsilon _{0}}{\mu _{0}}}\exp(j\left( k x-\omega t\right)) \\ &= \dfrac{E_{0}^{2}}{2}\sqrt{\dfrac{\varepsilon _{0}}{\mu _{0}}} \end{aligned}
物理的意味:単位時間内に単位面積を通過するエネルギー量
ポインティングベクトルの定義をそのまま記載しています。電磁波に限らず、成立します。
最後に
電磁波の問題は、電磁気学を試験科目とする大学の中でも範囲に含まれない場合があります。
京大、阪大、名大、電通大などでは出題されたことが無いです。一方で、東大、東北大、神戸大ではたまに出題されます。後者の大学群を志望される方は是非チェックしたい分野になります。
参考文献
新しい電磁気学:太田昭男(著) 第11章、12章