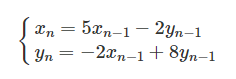下記の漸化式の一般項\(x_{n}、y_{n}\)を求めよ。ただし、\(n≧1、x_{0}=1、y_{0}=0\)とする。
\begin{cases}x_{n}=5x_{n-1}-2y_{n-1}\\ y_{n}=-2x_{n-1}+8y_{n-1}\end{cases}
はじめに
こちらの問題、皆様はどのようにして解きますでしょうか。カンの良い方は、\(n、n-1、n-2・・・\)と数を落としていき、最終的に初期値を代入して解くことを考えると思います。
しかし、手計算で何も考えずに数を落としていくには時間がかかりそうです。
このようなときどうすれば良いか。答えは行列です。もしかすると、行列がまだ高校教育範囲だったころ、大学受験で勉強された方も居るかもしれません。
大学院入試でも、大阪大学をはじめ出題されたことがあります。今一度復習する意味で本問をチェック下さると幸いです。
本記事で覚えたいこと
- \(\begin{pmatrix} x_{n} \\ y_{n} \end{pmatrix}=A\begin{pmatrix} x_{n-1} \\ y_{n-1} \end{pmatrix}\) 表記に漸化式を書き換える。
- \(\begin{pmatrix} x_{n} \\ y_{n} \end{pmatrix}=A^{2}\begin{pmatrix} x_{n-2} \\ y_{n-2} \end{pmatrix}=\ldots =A^{n}\begin{pmatrix} x_{0} \\ y_{0} \end{pmatrix}\)型までnを落とす。
- \(A\)を対角化し、\(A^{n}\)を求める。
- 初期値\(x_{0}、y_{0}\)を代入し、一般項を求める。
行列表記に落とし込めれば、後は繰り返し適用することで一般項を求められることが分かります。
漸化式を1変数分\(x_{n}=Ax_{n-1}\)のように与えられていると、繰り返し適用することは想像つくと思います。本問は2変数ですが、同じ考え方で解いていくことになります。
対角化についてはこちらの記事で説明しています。まだ方法を覚えていない方は、ぜひ参照してください。
解答例
与えられた漸化式は、以下のように行列表示できる。
\begin{eqnarray}\begin{pmatrix} x_{n} \\ y_{n} \end{pmatrix}=\begin{pmatrix} 5 & -2 \\ -2 & 8 \end{pmatrix}\begin{pmatrix} x_{n-1} \\ y_{n-1} \end{pmatrix}\end{eqnarray}
\(A=\begin{pmatrix} 5 & -2 \\ -2 & 8 \end{pmatrix}\)とし、\(A\)の固有値\(\lambda\)を求める。
\begin{align}&\begin{vmatrix}5-\lambda & -2 \\ -2 & 8-\lambda\end{vmatrix} \\ &=(5-\lambda)(8-\lambda)-4 \\ &=\lambda^{2}-13\lambda+36 \\ &=(\lambda -9)(\lambda -4) \\ &=0\end{align}
よって、固有値\(\lambda=4,9\)
(i)\(\lambda=4\)のとき、固有ベクトル\(v_{1}=\begin{pmatrix} 2 \\ 1 \end{pmatrix}\)
(ii)\(\lambda=9\)のとき、固有ベクトル\(v_{2}=\begin{pmatrix} 1 \\ -2 \end{pmatrix}\)
よって、\(P=\begin{pmatrix} 2 & 1 \\ 1 & -2 \end{pmatrix}\)とし、\(P^{-1}=\dfrac{1}{5}\begin{pmatrix} 2 & 1 \\ 1 & -2 \end{pmatrix}\)と計算できるため
\(A=PDP^{-1}\)と対角化できる。ただし、\(D=\begin{pmatrix} 4 & 0 \\ 0 & 9 \end{pmatrix}\)である。
\(A^{n}=PD^{n}P^{-1}\)で、\(D^{n}=\begin{pmatrix} 4^{n} & 0 \\ 0 & 9^{n} \end{pmatrix}\)のため、以下のように計算できる。
\begin{align}A^{n}&=\dfrac{1}{5}\begin{pmatrix} 2 & 1 \\ 1 & -2 \end{pmatrix}\begin{pmatrix} 4^{n} & 0 \\ 0 & 9^{n} \end{pmatrix}\begin{pmatrix} 2 & 1 \\ 1 & -2 \end{pmatrix} \\ &= \dfrac{1}{5} \begin{pmatrix} 2・4^{n} & 9^{n} \\ 4^{n} & -2・9^{n} \end{pmatrix}\begin{pmatrix} 2 & 1 \\ 1 & -2 \end{pmatrix} \\ &= \dfrac{1}{5} \begin{pmatrix} 4^{n+1}+9{n} & 2・4^{n}-2・9^{n} \\ 2・4^{n} – 2・9^{n} & 4^{n}+4・9{n} \end{pmatrix}\end{align}
\(\begin{pmatrix} x_{n} \\ y_{n} \end{pmatrix}=A^{n}\begin{pmatrix} x_{0} \\ y_{0} \end{pmatrix}\)であり、\(x_{0}=1、y_{0}=0\)のため
一般項\(x_{n}、y_{n}\)は第1列目の1行目、2行目の要素の値とそれぞれ等しくなる。
\begin{cases}x_{n}=\dfrac{4^{n+1}+9^{n}}{5}\\ y_{n}=\dfrac{2\cdot 4^{n}-2\cdot 9^{n}}{5}\end{cases}
最後に
解法さえ知っておけば、漸化式問題はワンパターンで解けることが多いです。本問が初見だった方は、是非とも解き方をマスターし、試験の際は得点源にしましょう。
参考文献