下記の図1.図2それぞれの伝達関数を求めよ。
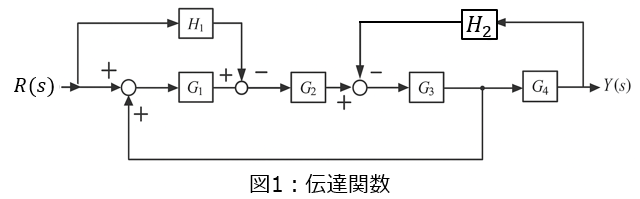
問1:入力$R(s)$に対する出力$Y(s)$の比$G_a$(図1)
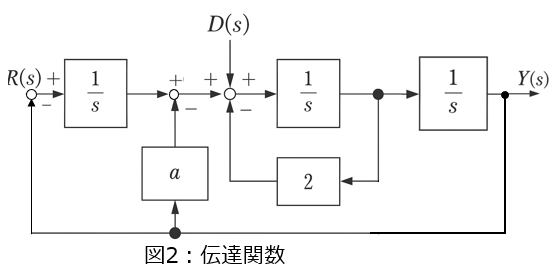
問2-1:入力$R(s)$に対する出力$Y(s)$の比$G_b$(図2)
問2-2:入力$D(s)$に対する出力$Y(s)$の比$G_c$(図2)
伝達関数の簡単化
院試や電検(2次試験)で制御の問題が出題されるとき、序盤で伝達関数を求めることがよくあります。よく教科書では、下記の表でまとめられています。
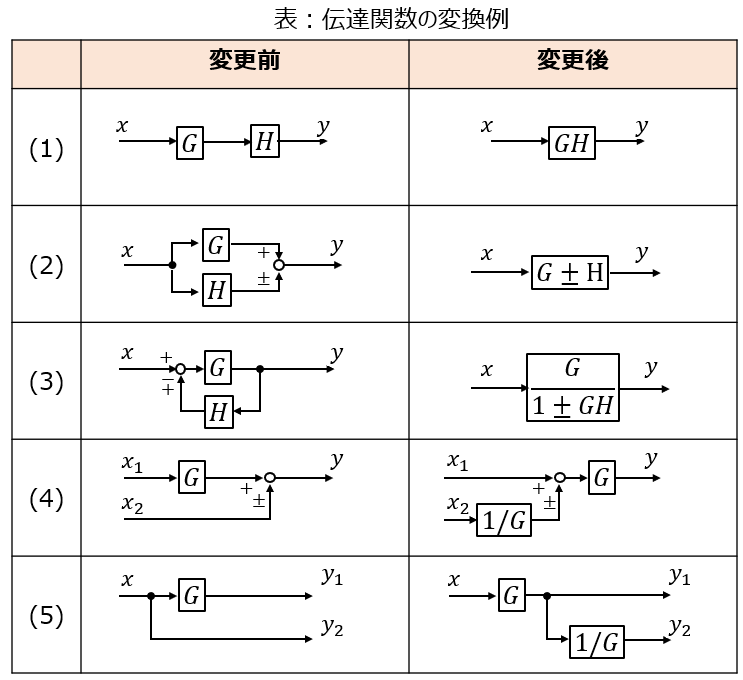
簡単な系ならば、上記の表に基づいたブロック線図の移動、簡単化の内容を丸暗記していても解けるかもしれませんが、本記事で上げるような複雑な系だと手こずる場合があります。そこで、本記事では、表を覚えていなくとも伝達関数を求められる方法を説明し、そのやり方で紹介した問題を解いていきたいと思います。
伝達関数の求め方
- ブロック線図の向きに合わせ、変数の乗算、加減算の関係を立式する。
長くなる場合は、信号の合流点部分に中間変数を設定し、方程式を分ける。
詰まるところ、システムの内容に合わせて信号の入出力関係を方程式にし、これを解けば良いわけですね。
計算内容自体は中学数学の領域です。図に基づいて正しく立式できるかにかかっています。
例として、表の(3)にあったフィードバック要素の伝達関数を簡単化してみましょう。

\begin{aligned}Y=(X±YH)G\end{aligned}
\begin{aligned}G=\dfrac{Y}{X}=\dfrac{G}{1±GH}\end{aligned}
このように、結果を覚えていなくとも、直接導出できます。
解答例
問1 伝達関数$G_a$の算出
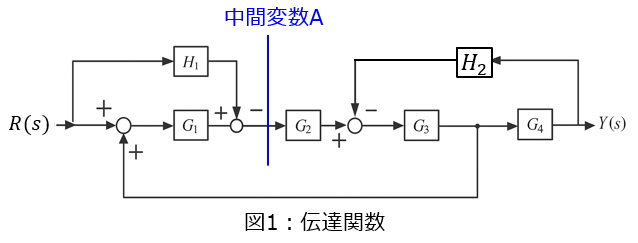
下記図のように、中間変数Aを$G_1,G_2$の間に設定する。
この場合、入出力関係は下記の方程式で表される。
\begin{cases}A=G_1 \left(R+\dfrac{Y}{G_4} \right)-H_1 R \\ Y=(AG_2-YH_2)G_3G_4 \end{cases}
第二式を変形し
\begin{aligned}Y=G_2G_3G_4A-H_2G_3G_4Y\end{aligned}
\begin{aligned}A=\dfrac{1+H_2G_3G_4}{G_2G_3G_4}Y\end{aligned}
第一式に代入し
\begin{aligned}(1+H_2G_3G_4)Y=G_1G_2G_3G_4\left(R+\dfrac{Y}{G_4}\right)-H_1G_2G_3G_4R\end{aligned}
\begin{aligned}(1+H_2G_3G_4-G_1G_2G_3)Y=G_2G_3G_4(G_1-H_1)R\end{aligned}
\begin{aligned}G_a&=\dfrac{Y}{R}\\ &=\dfrac{G_2G_3G_4(G_1-H_1)}{1+H_2G_3G_4-G_1G_2G_3}\end{aligned}
問2 伝達関数$G_b$の算出
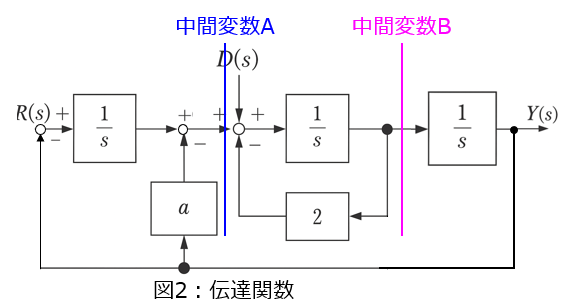
上図のように、中間変数$A,B$を設定する。$D(s)=0$と考えて良く
\begin{cases}A=(R-Y)・\dfrac{1}{s}-aY \\ B=(A-2B)・\dfrac{1}{s} \\ Y=\dfrac{B}{s}\end{cases}
第三式により、$B=sY$
これを第二式に代入し
\begin{aligned}s^{2}Y=A-2sY \\ A=s(s+2)Y\end{aligned}
これを第一式に代入し
\begin{aligned}s(s+2)Y=(R-Y)・\dfrac{1}{s}-aY\end{aligned}
\begin{aligned}(s^{3}+2s^{2}+as+1)Y=R\end{aligned}
\begin{aligned}G_b&=\dfrac{Y}{R} \\ &=\dfrac{1}{s^{3}+2s^{2}+as+1}\end{aligned}
問2-2 伝達関数$G_c$の算出
本問は、システムの入出力間に入力$D$が入っていることから外乱に対する伝達関数を想定しています。問2と同じ中間変数$A,B$を設定し、$R(s)=0$とすると
\begin{cases}A=-\dfrac{Y}{s}-aY \\ B=(A+D-2B)・\dfrac{1}{s} \\ Y=\dfrac{B}{s}\end{cases}
同じく、第三式により、$B=sY$
これを第二式に代入し
\begin{aligned}sY=(A+D-2sY)・\dfrac{1}{s}\end{aligned}
\begin{aligned}A=(s^{2}+2s)Y-D\end{aligned}
これを第一式に代入し
\begin{aligned}(s^{2}+2s)Y-D=-\dfrac{Y}{s}-aY\end{aligned}
\begin{aligned}(s^{3}+2s^{2}+as+1)Y=sD\end{aligned}
\begin{aligned}G_c&=\dfrac{Y}{D} \\ &=\dfrac{s}{s^{3}+2s^{2}+as+1}\end{aligned}