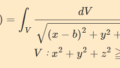同じ積分計算をフーリエ変換、ラプラス変換それぞれの方法で解く

(1)複素積分の考え方を利用し、下記の積分値を求めよ。
\begin{eqnarray}\int _{0}^{\infty }\dfrac{\cos tx}{1+x^{2}}dx\end{eqnarray}
ただし、積分路は下記(図1)を採用すること。

(2)ラプラス変換を利用し、下記の積分値を求めよ。\begin{eqnarray}\int _{0}^{\infty }\dfrac{\cos tx}{1+x^{2}}dx\end{eqnarray}
ただし、下記の式は自由に用いて良い。
\begin{align}&\int _{0}^{\infty }\dfrac{1}{a^{2}+x^{2}}=\dfrac{\pi }{2a} \\ &L\left[ \cos (tx)\right] =\int _{0}^{\infty }\cos (tx)e^{-st}=\dfrac{s}{s^{2}+x^{2}}\end{align}

はじめに
本記事で身に着けたいこと
解答例
最後に
参考文献

はじめに

同じ積分計算式をラプラス変換、フーリエ変換それぞれを利用して計算する問題です。

以前の記事では、フーリエ級数展開で同様の求値問題を紹介しました。今回は、変換Verです。

何か特有の値を代入し、求めたい式の値に近づける。が、求値問題の鉄則です。本問(フーリエ変換)もその例に漏れません。

本記事で身に着けたいこと

フーリエ変換を利用した積分問題

\begin{eqnarray}\int _{0}^{\infty }\dfrac{e^{itx}}{1+x^{2}}=\int _{0}^{\infty }\dfrac{\cos tx}{1+x^{2}}dx+i\int _{0}^{\infty }\dfrac{\sin tx}{1+x^{2}}dx\end{eqnarray}

と式変形できることに注目します。右辺第1項が本問で求めたい積分内容です。

分子に\(\sin\)、\(\cos\)項がある場合、積分しやすい\(e\)項に置き換える
積分対象が奇関数のとき、\(\sin\)項=0になり
\(\cos\)で行った積分結果 = \(e\)項で行った積分結果と一致
積分対象が偶関数のとき、\(\cos\)項=0になり
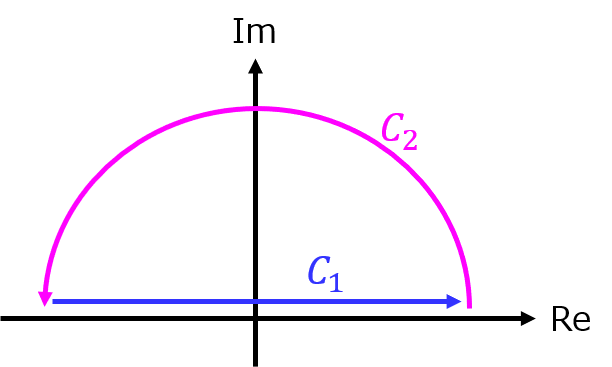
\(\sin\)で行った積分結果 = \(e\)項で行った積分結果と一致
\(e\)項で複素積分を実行。半径→∞を考えたとき、積分路\(C_{2}\)の結果が0になる。
複素積分結果=積分路\(C_{1}\)の結果のみになり、答えが求まる。

手順４．５．は、一般的な複素積分とやり方同じです。類題を他にも紹介していくつもりですので、他記事も通して経験を積んでいければと思います。

本記事で特に主張したいのは、１～３．です。

分子が\(e\)項になると留数を代入した後の計算が行いやすくなります。後の解答例で示します。

ラプラス変換を利用した積分問題

式(1)をラプラス変換すると、\begin{eqnarray}\int _{0}^{\infty }e^{-st}\left( \int _{0}^{\infty }\dfrac{\cos tx}{1+x^{2}}dx\right) dt\end{eqnarray}

になります。この式を以下の考え方で計算します。

手計算で積分可能な変数項に分けて積分する
積分結果を逆ラプラス変換し、結果を求める。

１．について、\(\int\)が2つもありますが、下記のように分けるとうまくいきそうです。

\begin{eqnarray}\int _{0}^{\infty }\dfrac{dx}{1+x^{2}}\int _{0}^{\infty }e^{-st}\cos txdt\end{eqnarray}

一つ目の\(\int\)は、(3)式を適用すること、二つ目の\(\int\)は(4)式を適用することで計算できそうです。

\(\cos(tx)\)が、\(x\)も\(t\)も両方変数を持っているので、1つ目、2つ目どちらの\(\int\)にも入れることができます。三角関数の項に分数が入ってしまうとラプラス変換が難しくなります。2つ目の\(\int\)に入れて公式適用すると楽に計算できます。

解答例

フーリエ変換を利用した場合

複素関数\begin{eqnarray}\int _{C_{1}+C_{2}}\dfrac{e^{itz}}{1+z^{2}}dz=\int _{C_{1}+C_{2}}\dfrac{\cos tz}{1+z^{2}}dz+i\int _{C_{1}+C_{2}}\dfrac{\sin tz}{1+z^{2}}dz\end{eqnarray}を考える。

\(\int _{C_{1}+C_{2}}\dfrac{\sin tz}{1+z^{2}}dz\)は奇関数のため、計算結果は0になる。

よって、\(\int _{C_{1}+C_{2}}\dfrac{e^{itz}}{1+z^{2}}dz=\int _{C_{1}+C_{2}}\dfrac{\cos tz}{1+z^{2}}dz\)になり、左辺の\(e\)項で積分を考えても良い。

極は、\(z=±i\)であり、閉路\(C_{1}+C_{2}\)内に存在するのは\(z=i\)。

留数定理より

\begin{eqnarray}Res_{z=i}\dfrac{e^{itz}}{1+z^{2}}=\dfrac{e^{-tz}}{2i}\end{eqnarray}を得る。

また、積分路\(C_{2}\)について、\(z=re^{i\theta}\)とし、\(r→∞\)の極限を考える。
(分母)→∞、(分子)→0のため、\(\int _{C_{2}}\dfrac{e^{itz}}{1+z^{2}}=0\)になる。

これより、\begin{eqnarray}\int _{C_{1}+C_{2}}\dfrac{e^{itz}}{1+z^{2}}=\int _{C_{1}}\dfrac{e^{itz}}{1+z^{2}}\end{eqnarray}になる。

コーシーの積分定理より、(5)式を使用して\begin{eqnarray}\int _{C_{1}+C_{2}}\dfrac{e^{itz}}{1+z^{2}}=\int _{C_{1}}\dfrac{e^{itz}}{1+z^{2}}=2\pi i \dfrac{e^{-t}}{2i}=\pi e^{-t}\end{eqnarray}

積分路\(C_{1}\)は、\(-∞<x<∞\)のため

\begin{eqnarray}\int _{-\infty}^{\infty }\dfrac{\cos tx}{1+x^{2}}dx =\pi e^{-t}\end{eqnarray}を得る。

本問で求められている積分範囲は\(0<x<∞\)で、積分対象は偶関数。よって、(12)式を1/2にすると

\begin{eqnarray}\int _{0}^{\infty }\dfrac{\cos tx}{1+x^{2}}dx =\dfrac{\pi}{2} e^{-t}\end{eqnarray}

ラプラス変換を利用した場合

(7)式に対し、式(4)を適用すると

\begin{eqnarray}\int _{0}^{\infty }\dfrac{1}{1+x^{2}}\cdot \dfrac{s}{s^{2}+x^{2}}dx\end{eqnarray}

これを部分分数分解し、式(3)を適用すると

\begin{align}&\dfrac{s}{s^{2}-1}\int _{0}^{\infty }\left( \dfrac{1}{1+x^{2}}-\dfrac{1}{s^{2}+x^{2}}\right) dx \\ &=\dfrac{s}{s^{2}-1}\left( \dfrac{\pi }{2}-\dfrac{\pi }{2s}\right) \\ &=\dfrac{s\pi }{s^{2}-1}\dfrac{s-1}{2s} \\ &= \dfrac{\pi }{2}\cdot \dfrac{1}{s+1} \end{align}

これより、\(L\left[\int _{0}^{\infty }\dfrac{\cos tx}{1+x^{2}}dx\right] = \dfrac{\pi }{2}\cdot \dfrac{1}{s+1}\)だから、これを逆ラプラス変換すると

\begin{eqnarray}\int _{0}^{\infty }\dfrac{\cos tx}{1+x^{2}}dx=\dfrac{\pi }{2}e^{-t}\end{eqnarray}を得る。