はじめに
加算器の回路設計は、院試頻出分野です。全加算器を使用し、桁上げ伝搬加算器を作成することが多いですが、計算時間が長い課題があります。
そこで、伝搬加算器を改良した先見加算器、保存加算器が出題されることがあります。
少し難しいですが、是非マスターして得点源になれば幸いです。
全加算器とは
2つの数値の和を2進数で求めるときに使用します。下記のようなシンボルになっています。
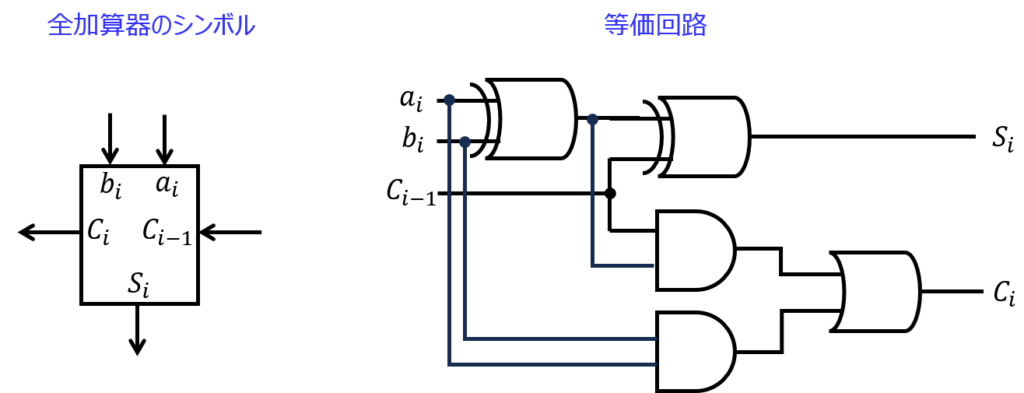
なお、nbitの数は、\(A:(a_{n-1},a_{n-2}, \ldots , a_{0}),B:(b_{n-1},b_{n-2}, \ldots ,b_{0})\)としています。
真理値表は下記のようになります。
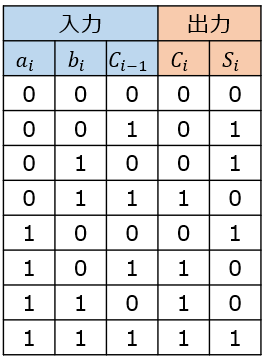
<$C_i$の論理式について>
下位bitからの繰上り$C_{i-1}=1$があり、対応するA,Bのbitの内、1つ以上1ならば桁上がり$C_{i}=1$が発生します。また、下位bitからの桁上がりが無くとも、A,Bのbitの内、両方が1ならば桁上がり$C_{i}=1$は同じく発生します。
<$S_i$の論理式について>
下位bitからの繰上りが無く$C_{i-1}=0$、A,Bのbitの内1つだけ1ならば\(S_{i}=1\)を出力します。また、全ての入力が1ならば、全ての出力\(C_{i},S_{i}\)が1になります。結局、3つの入力のうち、奇数個が=1ならば、$S_i=1$である整理ができます。
結論、それぞれの論理式は、下記のようになります。
\begin{cases}C_{i}=a_{i}b_{i}+\left( a_{i} \oplus b_{i} \right ) C_{i-1} \\ S_{i}= a_{i} \oplus b_{i} \oplus C_{i-1}\end{cases}
桁上げ伝搬加算器とは

全加算器を直列に繋いだものです。全加算器1つに付き、1bit分の計算を繰上り含めてできます。
これをn個直列に繋ぐと、最上位bitの桁上げ含め、nbit分の加算の計算ができます。一番右の列が0bit、左へ行く毎に1bit、2bitと続いていき、一番左が最上位bit(n-1bit)です。
原理は、私たちが行う筆算と同じです。一の位から足し算していき、桁上げを十の位へ渡すと思います。同じ操作です。
このように、一度理解してしまえば分かりやすい構成になっています。
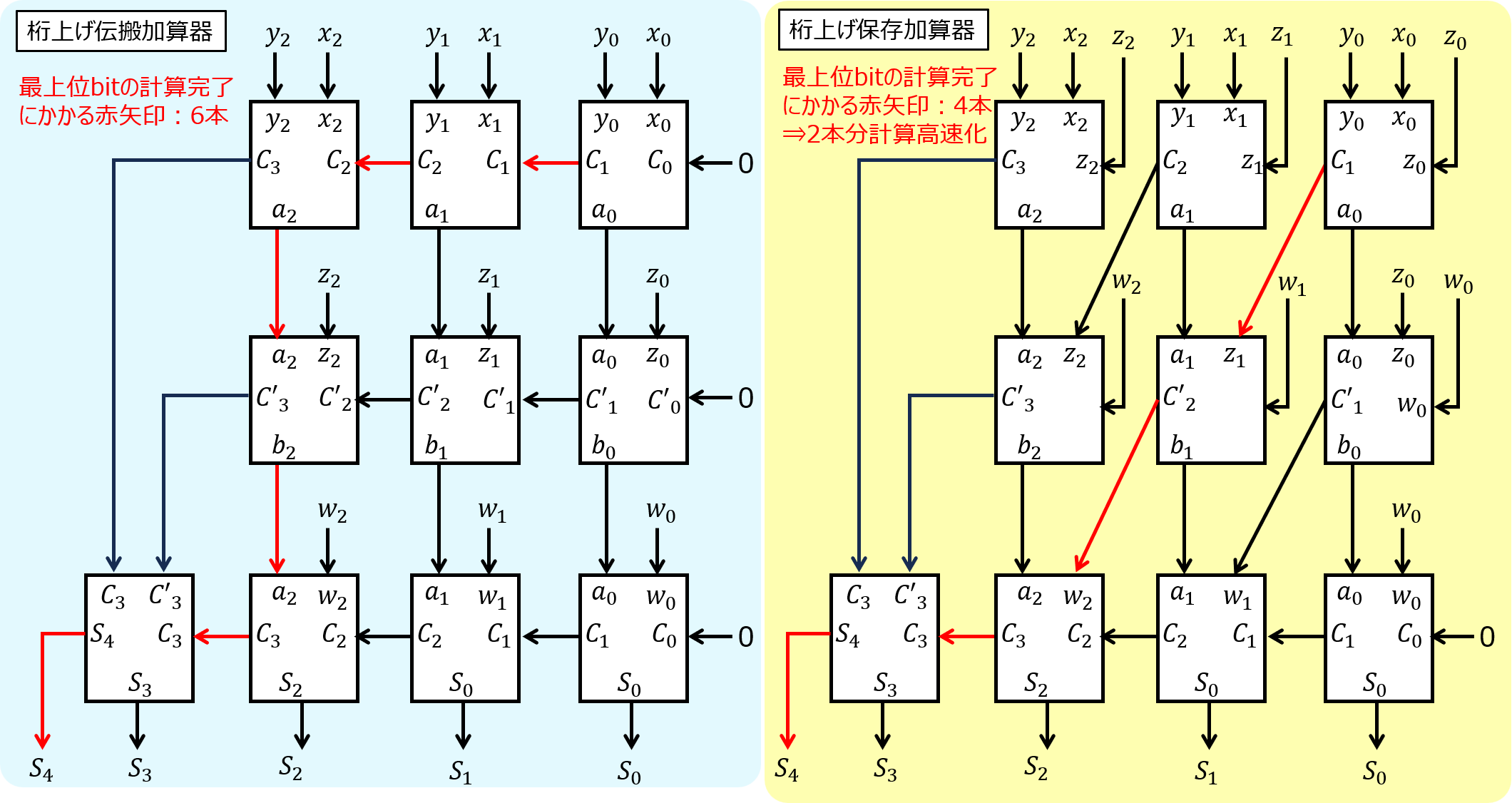
桁上げ伝搬加算器の欠点
計算に時間がかかることです。(クリティカルパスが長い)
nbit目の計算をするためには、n-1bit目で桁の繰上りが発生するか分からないといけないです。
同様に、n-1bit目の計算をするためには、n-2bit目で桁の繰上りが発生するか分からないといけないです。
n-2bit以下も同じことが言えますので、結局0bit目から順に計算していくしかありません。
このように、桁ごとに並列で計算することができません。
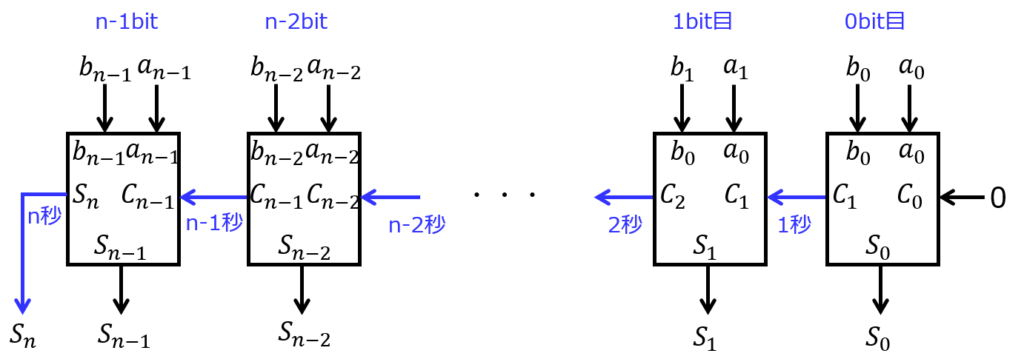
1bit計算する時間を1とすると、nbit計算完了するまで\(O(n)\)かかります。
次章で説明する桁上げ先見加算器は、この問題を改善したものになります。
桁上げ先見加算器の性質
桁上げ伝搬加算器は、漸化式(1)を\(i=0\)から順に反復計算していました。
先見加算器は、漸化式を展開した状態で回路を組みます。
例)2bitの場合
\begin{cases}C_{1}=a_{1}b_{1}+\left( a_{1}\oplus b_{1}\right) C_{0}\\ C_{0}=a_{0}b_{0}\\ S_{1}=\left( a_{1}\oplus b_{1}\right) \oplus C_{0}\end{cases}
\begin{cases}C_{1}=a_{1}b_{1}+\left( a_{1}\oplus b_{1}\right) a_{0}b_{0}\\ S_{1}=\left( a_{1}\oplus b_{1}\right) \oplus a_{0}b_{0}\end{cases}
初期値で与えられている\(A:(a_{1},a_{0}),B:(b_{1},b_{0})\)を用いて、全ての出力を計算できるため、伝搬時間が存在しないです。
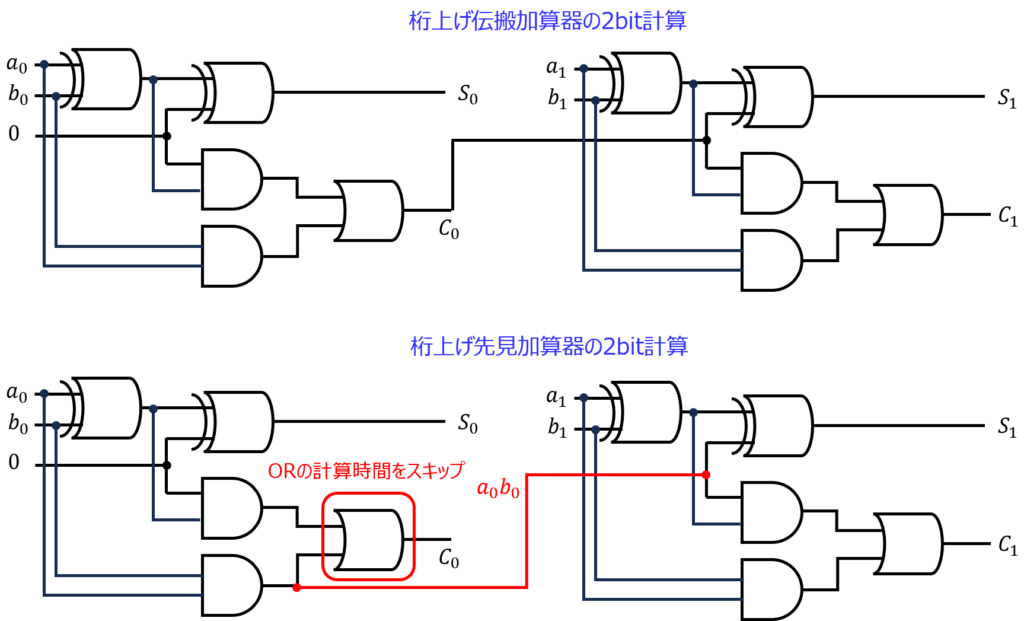
結局nbitの場合、以下で表すことができます。
\begin{eqnarray}C_{n}=\sum ^{n}_{j=0}\left( g_{j}\prod ^{n}_{k=j+1}p_{k}\right) +C_{-1}\prod ^{i}_{k=0}p_{k}\end{eqnarray}
ただし、\(C_{-1}\)は最下位bitへの繰り上げ入力です。\(g_{i},p_{i}\)はANDとXORです。
\begin{eqnarray}\begin{cases}g_{i}=a_{i}b_{i}\\ p_{i}=a_{i}\oplus b_{i}\end{cases}\end{eqnarray}
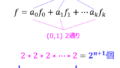
このようにすることで、n入力のゲートを用意できるならば、1段目で計算実行し、2段目で結果を足すことで、計算時間を大幅に低減することができます。
(一般項がnで表される漸化式をn=1になるまで展開し、その結果をn入力のゲートに全bit分入力すれば良いから。)
桁上げ先見加算器の欠点
低減できる計算時間量には限界があることです。前述により、nbitのゲートがあるならば、定数時間で計算できます。
しかし、ファンインの制限により、ゲートの入力数を際限なく増やすことができません。
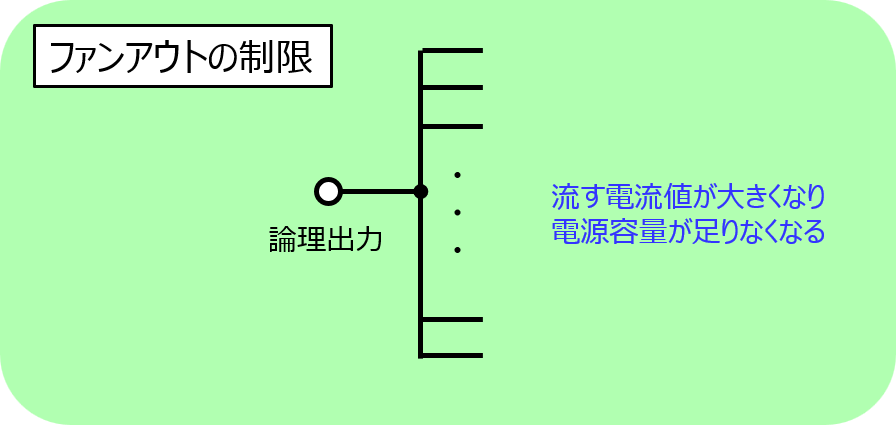
ファンインの制限とは
通常、論理回路は、PMOS,NMOS,トランジスタなどの半導体素子を使用します。電圧制御、電流制御で違いはありますが、入力数が増えると回路の抵抗値が極めて大きくなるか、小さくなります。これにより、期待通りの振る舞いができなくなります。
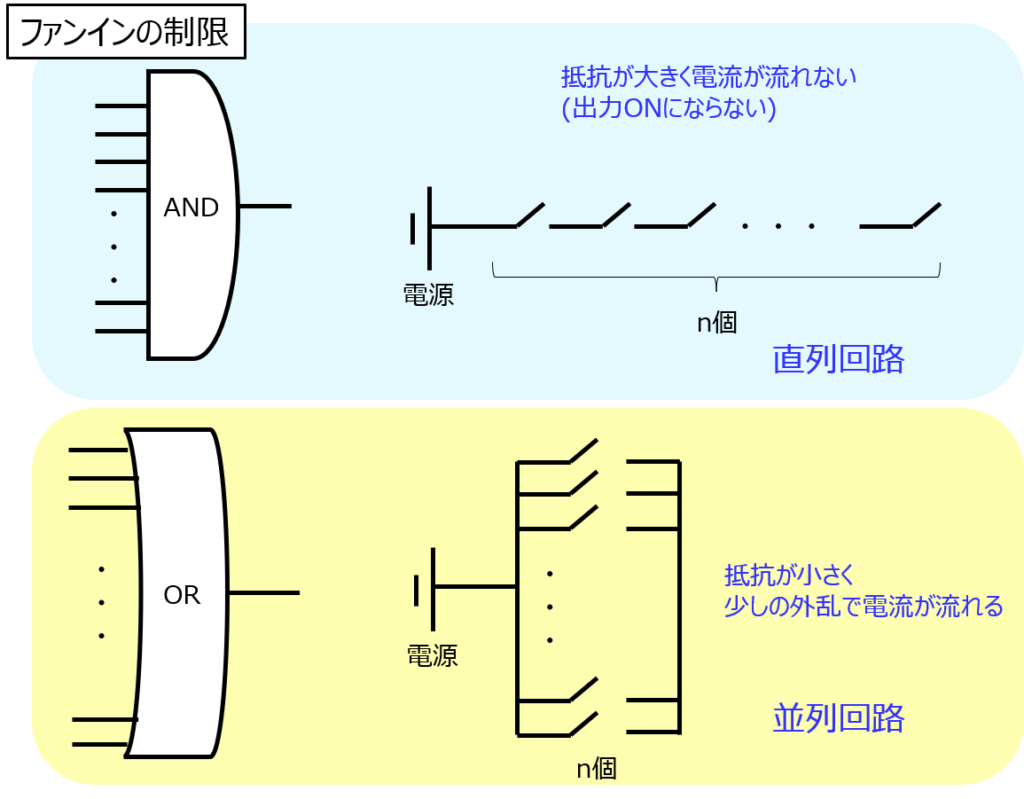
これが、ファンインの制限です。
先見加算器を作成する際は、この制限により、4bitずつ入力することが主流です。
同様に、出力側も無制限に大きくすることができません。これをファンアウトの制限と言います。
桁上げ保存加算器
今度は、3bitの4つの数X,Y,Z,Wを足し合わせることを考えます。
伝搬加算器で計算する場合、まずXとY,ZとWの和をそれぞれ求め、中間変数A,Bを算出。
A,Bを足し合わせることで最終結果を算出します。計算時間として、6周期かかります。
この計算時間を改善したものが、桁上げ保存加算器です。下記で表すことができます。
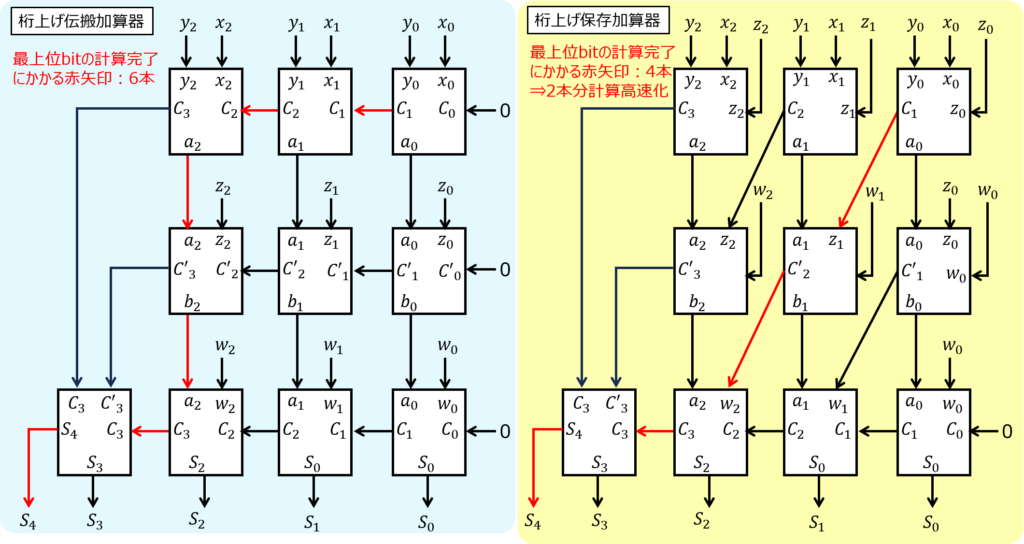
伝搬加算器では、上位bitへ桁上げを伝えるための遅延が発生しましたが、保存加算器は、桁上げ結果を各bitの下の段(本来Z,Wを加算する場所)にそれぞれ入力しています。
一方で、Z,Wは、それぞれ上の段で、桁上げフラグ\(C_{i}\)の代わりに代入することで、3bit加算を実現しています。
結局、一番下の段のみ伝搬が発生します。計算時間を4周期まで低減できました。
この性質は、乗算でも使用されていたりします。
最後に
本記事では、加算器の性質について説明しました。機会があれば、減算器や比較器についても紹介していきたいと思います。
参考文献
コンピュータハードウェア:情報系教科書シリーズ ; 第6巻 富田眞治(著), 中島浩共(著)