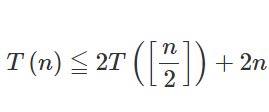n個の要素に対してある計算処理をする再帰関数\(T(n)\)がある。下記の不等式で表せるとき、計算時間をオーダー記法で算出せよ。ただし、[]はガウス記号で、[x]はxを超えない最大の整数を言う。また、\(T(1)=1\)とする。
\begin{eqnarray}T\left( n\right) \leqq 2T\left( \left[ \dfrac{n}{2}\right] \right) +2n\end{eqnarray}
はじめに
計算時間を議論するアルゴリズム分野は、Qiitaなどの素晴らしいサイトで多数の解説がなされています。(管理人も参考にさせていただいています。)
そのため、本記事で紹介する内容がどこかにあるかもしれません。それでも、再帰関数を分解し、計算時間の見積もりをする行為は、ソフト作成において非常に重要な作業になります。本記事では、再帰式からの計算時間量の見積もり方法について紹介します。
大枠の解き方
高校時代、漸化式の問題を解く際に、nの一般項、(n-1)の一般項…とn=1になるまで関数を展開していくことがあったと思います。本問も同様にして解いていきます。
ただし、展開するにあたり下記2つの方針があります。
方針1:n=1になるまで展開。その時の式を変形し計算時間の見積もりができる形に直す
\begin{eqnarray}T\left( n\right) \leqq 2T\left( \left[ \dfrac{n}{2}\right] \right) +2n\end{eqnarray}に対し、\begin{eqnarray}T\left( \dfrac{n}{2}\right) \leqq 2T\left( \left[ \dfrac{n}{2^{2}}\right] \right) +n\end{eqnarray}だから
\begin{align}T\left( n\right) &\leqq 2T\left( \left[ \dfrac{n}{2}\right] \right) +2n\\ &\leqq 2^{2}T\left( \left[ \dfrac{n}{2^{2}}\right] \right) +2*2n\\ &\ldots \\ &\leqq 2^{k}T\left( \left[ \dfrac{n}{2^{k}}\right] \right) +2nk\end{align}
ここで、ガウス記号を外すことを考えます。定義から
\begin{eqnarray}&1\leqq \dfrac{n}{2^{k}} <2\\ \Leftrightarrow &2^{k}\leqq n <2^{k+1}\end{eqnarray}のとき、\(T[ \dfrac{n}{2^{k}}]\)=1になる。
よって、\(k=\log_{2}n\)の条件下だと
\begin{eqnarray}T(n) \leqq 2^{k}T[1] +2nk \\ = n+2n \log_{2}n \end{eqnarray}
と最終的に行きつきます。
オーダー記法はnの次数が一番大きい項を取るので、T(n)の計算時間は
\(T(n)=O(n \log n)\)となる。
厳密性を期すならば数学的帰納法で確認した方が良いかもしれません。(与えられた不等式を忠実に展開しただけなので、管理人は不要と考えます。)
方針2:nを展開しやすい形に置き換えて計算する
こちらも再帰式を展開する方針は変わりませんが、\(n=2^{k}\)を代入してから展開します。
ガウス記号の中身は2で割り続けることに注目し、2を因数に持つ項をあらかじめ代入することがポイントです。こうすれば、\(\dfrac{2{k}}{2}\)が割り切れないことはありません。
方針1では、展開し終えた後の式の形に注目し、そこから\(n=2^{k}\)を代入していました。
今回は、予め2^{k+1}を代入し、展開後に行っていた式の評価を予め行う手番になっています。
よって、ガウス記号が最初から外れてT(1)まで展開した最後に大小比較の評価が入りません。よって、こちらの方が計算が楽になります。
\begin{align}T\left( 2^{k}\right) &\leqq 2T\left( 2^{k-1}\right) +2\cdot 2^{k}\\ &\leqq 2^{2}T\left( 2^{k-2}\right) +3-2^{k}\\ &\ldots \\ &\leqq 2^{k}+2k\cdot 2^{k}\end{align}
\(2^{k}+1,\quad 2^{k}+2\)など、\(2^{k+1}\)を超えない自然数が加算された場合を考えなくてよいのかという議論もあるかもしれません。
これは、ガウス記号の性質を利用しています。
(\(n=2^{k}+2^{k}-1\)を代入した場合でも、\(\left[\dfrac{2^{k}+2^{k}-1}{2}\right]=\dfrac{2^{k}}{2}\)となり、同じ結果になる。)
補足
冒頭で与えた再帰式は、マージソート(分割統治法)に似ています。
(2ブロックに分割後の計算時間)+(ソート完了後のマージする時間n)を
右辺 \(2T\left( \left[ \dfrac{n}{2}\right] \right) +2n\)で表現しています。このことに気づいている場合は、結果のO(nlogn)を簡単に導けたかもしれません。
また、問題によっては、漸化式の中身がガウス記号(床関数)ではなく、天井関数\(\lceil \rceil\)で与えられることがあります。
この場合は、本問のように、小数点以下を切り捨てではなく、切り上げになります。計算オーダーが増加する場合もありますので、記号の内容を注意深く確認することが重要です。
最後に
アルゴリズム論で勉強する計算時間設計は、情報系の学生だけでなく、万人の学生に勉強頂きたい分野と考えています。
会社に入ると、計算負荷、計算時間を勘案したプログラム実装が求められるためです。
参考文献
Cによるアルゴリズムとデータ構造 茨木 俊秀(著) P121