【PN接合】拡散電位(ビルトインポテンシャル)の導出

問題

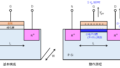
下記のPN接合ダイオードの拡散電位\(V_{bi}\)を導出せよ。ただし、接合面をx=0とし、空乏層領域を\(-x_{p}≦x≦x_{n}\)とする。ただし、アクセプタ密度を\(N_{p}\)、ドナー密度を\(N_{d}\)、半導体内の誘電率を\(\varepsilon\)、電荷量を\(q\)とする。

はじめに
要点
解答例
最後に
参考文献

はじめに

有名な問題ですが、結果のみの記載で、過程まで導出しているサイトが見当たりませんでした。

探せば、ネットで公開されている講義のレジュメにはありましたが、該当箇所を見つけるには少し時間がかかります。

今後、半導体デバイスの難しめの問題を紹介していく上での基本的な考え方が詰まっており、院試頻出分野になります。

そのため、上記の問題を、半導体デバイスにおける一つ目の記事として紹介したいと思います。

要点

電気的中性条件により、\(N_{p}\)と\(N_{d}\)の関係式を導く
ポアソン方程式を、p型領域、n型領域に適用する。
ポアソン方程式を積分し、電場\(E\)、電位\(V\)を\(x=0\)の境界条件の元に導く

基本的に、上記の計算をすることで8割方の問題に対応できると思います。

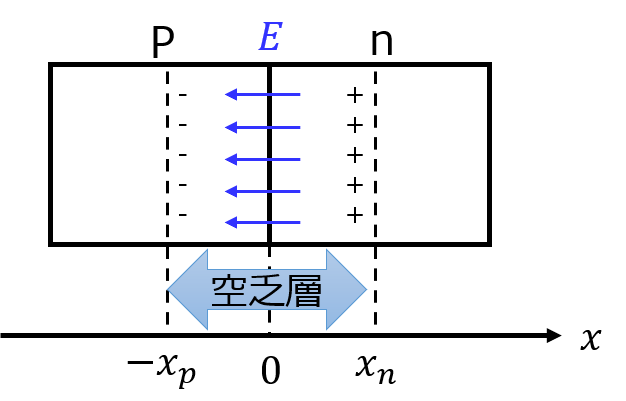
物理的な振る舞いは以下のようになっています。

１．p型半導体の多数キャリアは正孔(+)。n型半導体の多数キャリアは電子(-)のため、接合面を中心に両者が打ち消しあい、空乏層が発生します。

２．空乏層との境界面でp型は負、n型は正に帯電します。(多数キャリアが消滅しているので、少数キャリア側の電荷の符号に帯電する。)

３．正と負の電荷が発生しているので、両者の間に電場が発生。電位も発生する。

以上の電磁現象を、ポアソン方程式を使用すれば具体的な物理量まで求めることができます。

解答例

手順1 電気的中性条件

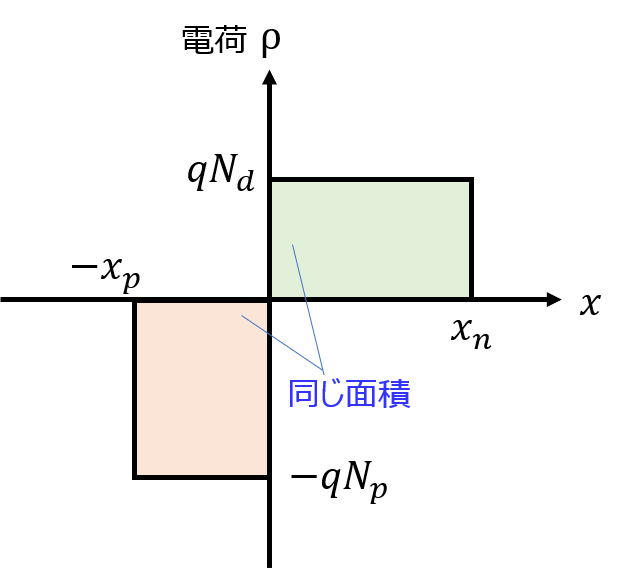
電気的中性条件により、\begin{eqnarray}qN_{p}x_{p}&=qN_{d}x_{d} \\ N_{p}x_{p}&=N_{d}x_{d} \end{eqnarray}

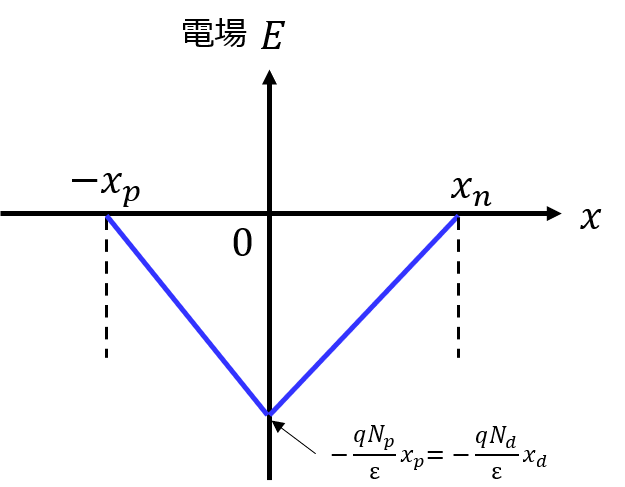
手順2,3 ポアソン方程式の適用

次に、電場を求める。

ポアソン方程式により、\begin{eqnarray}\frac{d^{2}V}{dx^{2}}=-\frac{\rho}{\varepsilon }\end{eqnarray}

電場、電位の定義より、\begin{eqnarray}E=-\dfrac{dV}{dx}\end{eqnarray}だから、上式を整理すると

\begin{eqnarray}\frac{dE}{dx}=\begin{cases}-\dfrac{qNp}{\varepsilon }\left( -x_{2}\leq x\leq 0\right) \\ -\dfrac{qN_{d}}{\varepsilon }\left( 0\leq x\leq x_{n}\right) \end{cases}\end{eqnarray}と表される。

これを積分し、\(-x_{p}≦x≦0\)のとき

\begin{eqnarray}E_{1}\left( x\right) =-\frac{qN_{p}}{\varepsilon }x+C_{1}\end{eqnarray}になる。

境界条件として、\(x=-x_{p}\)のとき、\(E_{1}(x)=0\)なので\(C_{1}=-\frac{qN_{p}}{\varepsilon }x_{p}\)が分かる。

これより、

\begin{eqnarray}E_{1}\left( x\right) =-\frac{qN_{p}}{\varepsilon }\left( x+x_{p}\right)\end{eqnarray}

を得る。

同様にして、\(0≦x≦x_{n}\)の範囲において

\begin{eqnarray}E_{2}\left( x\right) =\frac{qN_{d}}{\varepsilon }\left( x-x_{n}\right)\end{eqnarray}

となる。

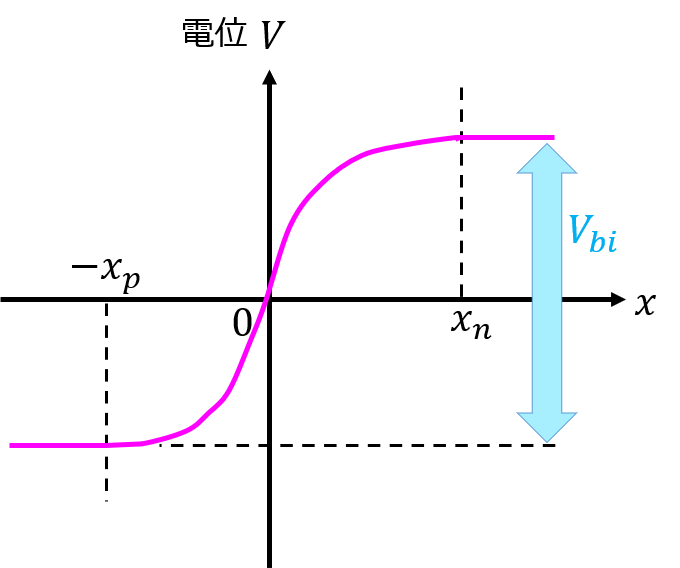
次に、\(E_{1}、E_{2}\)を積分し、\(V_{bi}\)を求める。(電位の基準は、\(x=0\)のとき、\(V=0\)とする。)

まず、\(E_{1}\)をxについて積分し

\begin{eqnarray}V_{1}(x)=-\int ^{x}_{0}-\frac{gN_{p}}{\varepsilon }( x+x_{2}) dx\\ =\frac{qN_{2}}{\varepsilon }( \frac{1}{2}x^{2}+x_{2}x) +C_{3} \end{eqnarray}

であり、境界条件を考える。

\(x=0\)のとき、\(V=0\)だから、\(C_{3}=0\)が分かり

\(x=-x_{p}\)のとき、\begin{eqnarray}V_{1}(-x_{p})=-\frac{qN_{p}}{2\varepsilon }x_{p}^{2}\end{eqnarray}

が得られた。次に、\(E_{2}\)分を考える。

\(E_{1}\)と同様にして、xについて積分し

\begin{eqnarray}V_{2}(x) &=-\frac{qN_{d}}{2\varepsilon }x( x-2x_{n}) \end{eqnarray}

\begin{eqnarray} V_{2}( x_{n}) &=\frac{qN_{d}}{2\varepsilon }x_{n}^{2}\end{eqnarray}

と求めることができる。

以上より、求める拡散電位(ビルトインポテンシャル)\(V_{bi}\)は、

\begin{eqnarray}V_{bi}=-V_{1}(-x_{p})+V_{2}(x_{n})=\frac{q}{2\varepsilon }( N_{p}x_{p}^{2}+N_{d}x_{d}^{2})\end{eqnarray}

であることが分かった。

※もし、空乏層幅\(x_{p}+x_{n}\)の算出も求められているときは、電気的中性条件により、求めた式(1)を使用すれば\(x_{p} , x_{n}\)いずれかの文字で表すことができます。