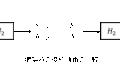下記図の矩形パルス\(g(t)\)のフーリエ変換\(G(f)\)を低域通過フィルタ\(H(f)\)に入力したときの出力を求めたい。次の問に答えよ。
(1)\(g(t)\)のフーリエ変換\(G(f)\)を求めよ。また、\(\tau\)を0に近づけた時どのようになるか説明せよ。
(2)\(g(t)\)を基本周期とする周期Tの周期関数をフーリエ級数で表せ。ただし、下記の公式を用いて良い。
\begin{cases}a_{n} &=\dfrac{2}{T}\int _{-\infty }^{\infty }f\left( t\right) \cos \left( \dfrac{2 \pi n t}{T}\right)dt \\ b_{n} &=\dfrac{2}{T}\int _{-\infty }^{\infty }f\left( t\right) \sin \left(\dfrac{2 \pi n t}{T} \right)dt \end{cases}
(3)\(H(f)\)に\(g(t)\)を入力したときの出力\(y(t)\)を求めよ。ただし、\(\dfrac{1}{T}<B<\dfrac{2}{T}\)とする。

パルス幅変調(PAM)とは
ある周波数\(f_{m}\)の信号周期\(T≦\frac{1}{2f_{m}}\)ごとに標本化し、パルス状の波形を持つ信号に変換することを言います。(PAM:Pulse Amplitude. Modulationの略です。)
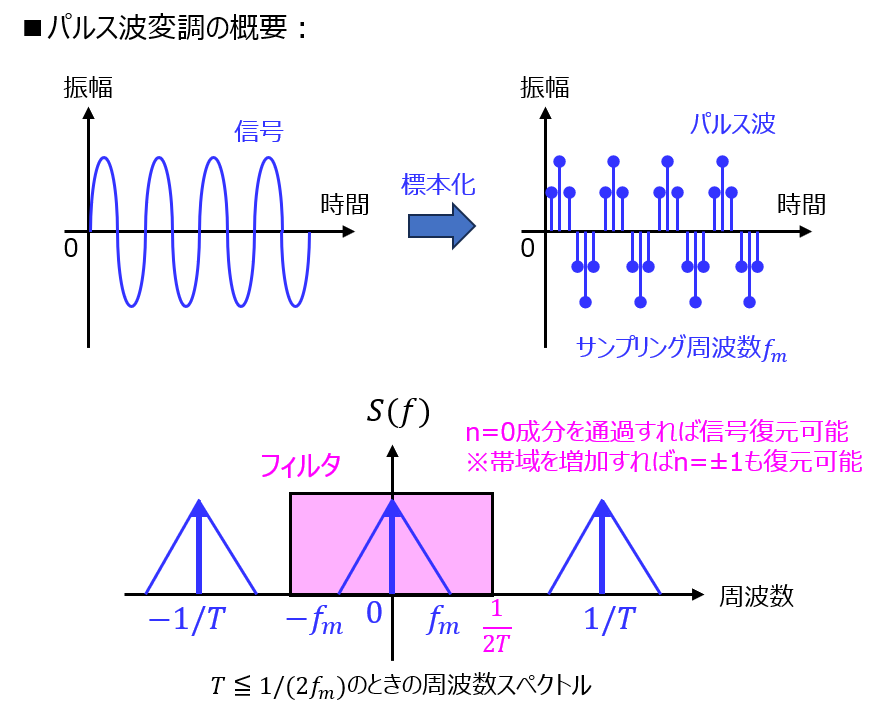
標本化した後の信号は、帯域幅が\(\dfrac{1}{2T}\)以下の低域通過フィルタを用いれば、元の波形のみ復元できます。
受信側では、周期Tでサンプリングしていることが分かっています。そのため、受信した信号を周期Tで逆の処理をすれば、復元することができます。
パルス変調波形(PAM)の表現方法
フーリエ級数を用います。
\begin{aligned}g(t)=\sum ^{\infty }_{n=-\infty }g\left( nT\right) \delta \left( t-nT\right)\end{aligned}
のように表現できれば、nは整数でデルタ関数を重ね合わせているため、パルス波を表現できます。
パルス変調波形(PAM)の復調方法
復調後の波形を\(y(t)\)とし、フィルタ\(H(f)\)の時間領域表記を\(h(t)\)とすると、下記で表すことができます。
\begin{aligned}y(t)=\sum^{\infty}_{n=-\infty}g(nT)h(t-nT)\end{aligned}
これは、下記の畳み込み積分の関係から来ています。(\(n\)は整数)
\begin{aligned}y(t)=\int^{\infty}_{-\infty}g(\tau)h(t-\tau)d\tau\end{aligned}
g(t)は\(t=nT\)でのみ値を持つ離散時間信号なので、(3)式になります。
なお、フィルタ\(H(f)\)の帯域が広いほど、\(y(t)\)で出力する\(g(nT)\)の整数nが多くなります。(3)で説明します。
解答例
(1)パルス波のフーリエ変換
\begin{aligned}G(f)&=\int^{\frac{\tau}{2}}_{-\frac{\tau}{2}}\dfrac{1}{\tau}e^{-j2\pi f t}dt \\ &= \left[ \dfrac{e^{-j2\pi f t}}{-j2 \pi f} \right]^{\frac{\tau}{2}}_{-\frac{\tau}{2}} \\ &=\dfrac{\sin(\pi f t)}{\pi f t} \end{aligned}
\(\tau→0\)のとき、\(\dfrac{\sin(x)}{x} \fallingdotseq 1\)だから
\begin{aligned}G(f) \fallingdotseq 1\end{aligned}
単位インパルス関数になる。
(2)\(g(t)\)のフーリエ級数
問題文で与えられた公式より、矩形波の範囲は\(-\frac{\tau}{2}≦t≦\frac{\tau}{2}\)なので
\begin{cases}a_{n} &=\dfrac{2}{T}\int _{-\frac{\tau}{2} }^{\frac{\tau}{2} }g\left( t\right) \cos \left( \dfrac{2 \pi n t}{T}\right)dt \\ b_{n} &=\dfrac{2}{T}\int _{-\frac{\tau}{2} }^{\frac{\tau}{2} }g\left( t\right) \sin \left(\dfrac{2 \pi n t}{T} \right)dt \end{cases}
で、\(g(t)\)は偶関数なので、\(b_{n}=0\)
\(a_{n}\)について、問(1)の結果を利用し
\begin{cases}a_{0}&=\dfrac{1}{T} \\ a_{n}&=\dfrac{2}{T}\dfrac{\sin(\pi n \tau t)}{\pi n \tau t}\end{cases}
よって、\(g(t)\)のフーリエ級数は
\begin{aligned}g(t)=\dfrac{1}{T} + \dfrac{2}{T}\dfrac{\sin(\pi n \tau t)}{\pi n \tau t}\cos\left(\dfrac{2\pi n t}{T}\right) \end{aligned}
(3)低域通過フィルタを通した時の出力信号\(y(t)\)
フィルタの帯域\(\dfrac{1}{T}<B<\dfrac{2}{T}\)について、\(f<B<2f\)と書き換えられる。
Bは絶対値なので、周波数0,±fのフーリエ級数を持つ\(g(t)\)がフィルタを通過する。\(n=-1,0,1\)の成分が対応する。
よって、出力信号は下記になる。
\begin{aligned}g(t)=\dfrac{1}{T} + \dfrac{4}{T}\dfrac{\sin(\pi \tau T)}{\pi \tau T}\left(\dfrac{2\pi n t}{T}\right)\end{aligned}
最後に
本問は、あまり院試では出ないかもしれません。
ただ、背景知識として出題されることがあります。
通信工学が試験範囲の大学院を受験される方は、是非理解しておくと良いです。