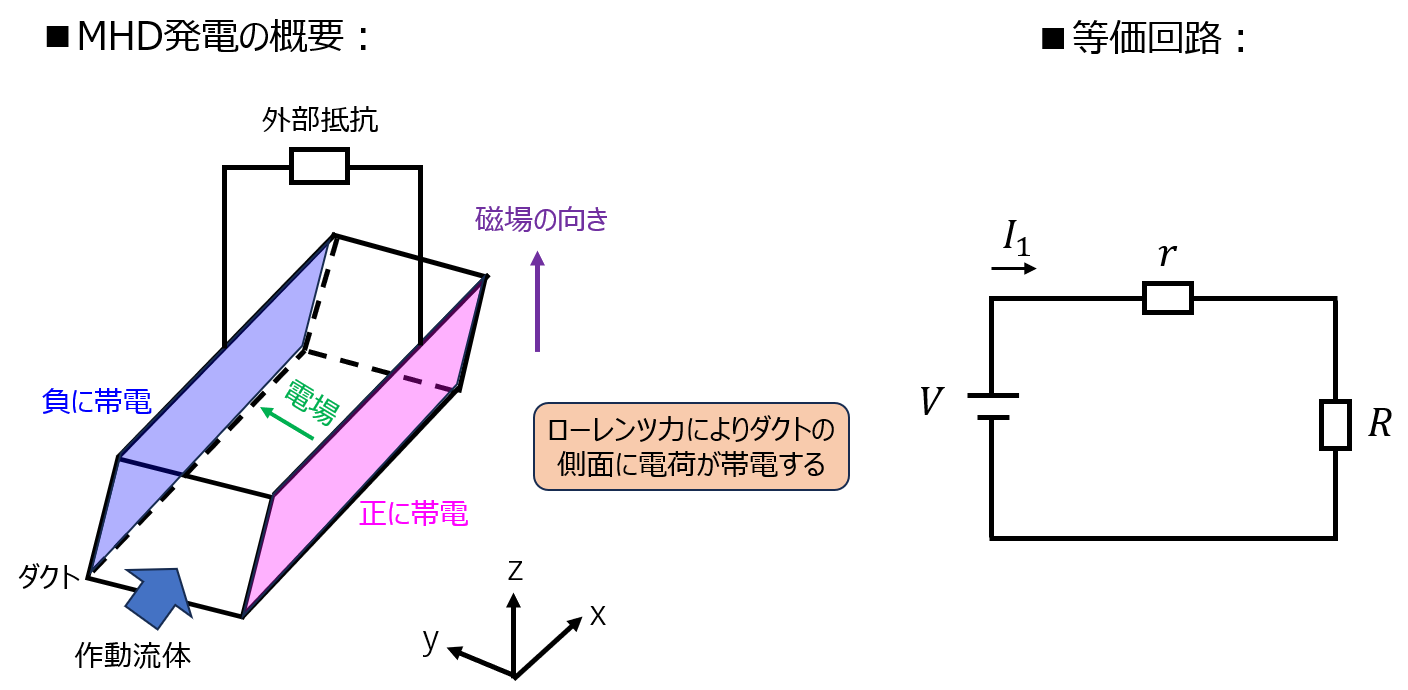
図1は、MHD発電の原理を説明するものである。図に示す方向にデカルト座標系をとり、x,y,z軸方向の単位ベクトルを、それぞれ\(\boldsymbol{e_{x}},\boldsymbol{e_{y}},\boldsymbol{e_{z}}\)で表す。速度\(\boldsymbol{v}=u\boldsymbol{e_{y}}\)の導電性の差動流体が、\(\boldsymbol{e_{y}}\)方向に延びる幅\(d\)の方形ダクトに流入する。ダクト内には、磁束密度\(\boldsymbol{B}=B\boldsymbol{e_{z}}\)の磁場が印加されている。ダクトの両側面には電極対a,bが設置され、負荷(抵抗値\(R\))に接続されている。
(1)作動流体に生じる起電力の大きさを求めなさい。
(2)電極対間の作動流体の抵抗値を\(r\)として、負荷にかかる電圧および流れる電流の大きさをそれぞれ求めなさい。また、負荷が消費する電力も求めなさい。
(3)(2)の電流は作動流体にも流れていることを考慮して、作動流体が受ける力の大きさを求めなさい。また、作動流体が単位時間あたりになす仕事を求めなさい。
(4)(2),(3)の結果を用いて、この動作状態にある発電機の効率を求めなさい。
MHD発電とは
Magneto Hydro Dynamicの略で、導電性の流体を磁場を用いて捕集し、電気を出力する発電方法です。(電磁流体発電とも呼ばれます。)
石炭、天然ガスなどを利用し温めた高温流体を磁界の中で通すことで、誘導起電力が発生。これにより発電できます。
通常の火力発電は、タービンに相当する回転子が存在しますが、本発電形式ではこれが不要になります。また、前者は交流で出力するに対し、MHD発電は直流で出力します。
また、電磁誘導を発生しやすくするために、高温流体中にカリウム、セシウムなどの分子をドープします。この結果、燃料中の硫黄と結合し、ドープ物質の回収装置を一緒に回収できるので、環境負荷が小さいです。
ホール効果と似ていますが、ホール効果は半導体の物性測定に用いられるのに対し、MHD発電は発電を目的としています。
発電の概要
下記に発電器の概要図と等価回路を示します。
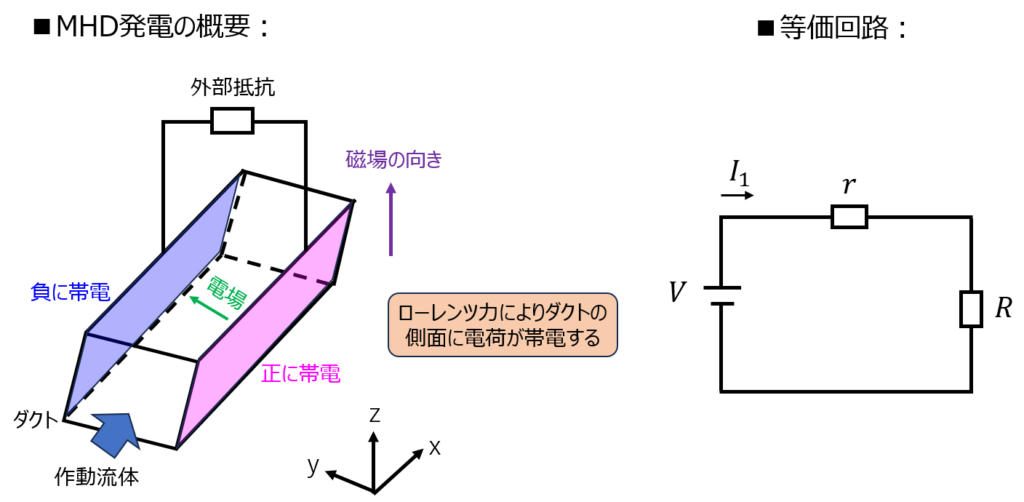
発電機は、導電性流体(作動流体)を通すためのダクトがあり、ダクト内には鉛直方向の磁場が一様にかかっています。
作動流体は、ダクト内でフレミング左手の法則がかかり、負の電荷は+y方向、正の電荷は-y方向に流れます。
この結果、ダクトの側面には正負の電荷がかかり、電場が発生することから、起電力も発生します。
これを外部回路に繋いで電気出力を得るということですね。
等価回路で表すと非常にシンプルです。外部回路の抵抗\(R\)と内部抵抗\(r\)の直列回路で示されます。
次章(解答例)では、発電に関するパラメータを定量的に求めていきます。
解答例
(1)作動流体にかかる起電力
フレミング左手の法則より、電子は+y方向に負に帯電する。
電場は一定であるため、求める起電力は
\begin{aligned}V=vBd\end{aligned}
(2)負荷にかかる電圧、電流、電力
負荷にかかる電圧を\(V_{L}\)電流を\(I_{L}\)とすると
\begin{cases}V_{L}=\dfrac{R}{R+r}V =\dfrac{R}{R+r}vBd \\ I_{L}=\dfrac{vBd}{R+r}\end{cases}
これより、求める消費電力\(P_{L}\)は
\begin{aligned}P_{L}=V_{L}I_{L}=\dfrac{R}{(R+r)^{2}}(vBd)^{2}\end{aligned}
(3)作動流体の力の大きさ
ダクト内に発生する電場の大きさは
\begin{aligned}E&=\dfrac{V-V_{L}}{d} \\ &=vB-\dfrac{R}{R+r}vB \\ &=\dfrac{r}{R+r}vB\end{aligned}
これより、作動流体が受ける力の大きさは
\begin{aligned}|\boldsymbol{F}|&=|\boldsymbol{J}×\boldsymbol{B}| \\ &=\dfrac{\sigma r}{R+r}vB^{2}\end{aligned}
単位時間当たりの仕事uは
\begin{aligned}u=Fv=\dfrac{\sigma r}{R+r}v^{2}B^{2}\end{aligned}
(4)MHD発電の効率計算
(3)より、作動流体がダクト内全体で行う仕事Uは
\begin{aligned}U=ud\end{aligned}
\(\sigma=\dfrac{d}{r}\)なので
\begin{aligned}U=\dfrac{1}{r}\left(\dfrac{r}{R+r}\right)(vBd)^{2}\end{aligned}
効率\(\eta\)は、消費電力\(P_{L}\)に対する比を取れば良いので
\begin{aligned}\eta=\dfrac{P_{L}}{U}&=\dfrac{R}{(R+r)^{2}}・(R+r) \\ &=\dfrac{R}{R+r}\end{aligned}
補足
MHD発電で利用した燃料ガスを火力発電に再利用することで、発電の総合効率を50~60%にまで高めることができます。