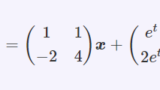東工大(東京科学大学) 電気電子系 院試の全体
電気数学、電磁気学、電気回路(電子回路有)、量子力学/物性基礎で構成されています。
試験時間は160分(9:30-12:10)です。英語はTOEICによる点数換算で、全科目合わせて合計950点満点になっています。
<必須科目>
- 電気数学(300点)
- 電磁気学(300点)
- 英語(150点)
<選択科目> 2科目中1科目選択
- 電気回路(電子回路有)(200点)
- 量子力学/物性基礎(200点)
各科目の概要
電気数学
解析学(微分方程式含む)、複素関数(フーリエ変換)からの出題が非常に多いです。他大学のように、一問一答型ではなく、誘導付きで小問ごとに解いていきます。問い自体はオーソドックスな問題が多いです。
一方で、線形代数、ベクトル解析、確率統計はあまり出題されません。最後まで出題された年は平成まで遡ります。併願先の兼ね合いもありますが、対策は少なめで良いと思います。
目標
電気系科目(電磁気学、電気回路)の出来にもよりますが、全体としては、6,7割欲しいセットですね。
試験対策に役立つ記事
数学
対策に使える参考書、問題集
全体
最近5か年は以下の分野の出題がありました。
- 2023年:
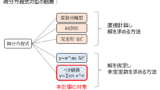
- 微分方程式と級数展開
- 複素関数と軌跡、積分
- 2022年:
- 微分方程式と極値
- 関数とテイラー展開。極限の計算。
- 2021年:
- フーリエ変換と微分方程式の解法
- 微分方程式と一般解(小問集合)
- 2020年:
- コロナにより、問題開示無し。
- 2019年:
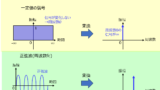
- フーリエ変換と周波数スペクトルの図示
- 不定積分と変数変換を利用した微分方程式の解法
数学のオススメ教科書、問題集
他科目にも言えることですが、まず第一に、東工大のシラバスサイトで掲載されている資料を読み込んだ方が良いです。類題が試験に出題されることもありますので、やらない手はありません。
その上で、周辺知識を補強する位置づけで紹介します。
線形代数
前述の通り、あまり出題は無いです。所属している大学で購入した教科書を見返すだけで良いと思いますが、一応シラバスで紹介されている教科書を紹介します。
一般教養のため、担当教員によって設定する書籍が異なります。
工学のための線形代数 村山光孝 (数理工学社)
普通です。強くオススメするほどのものでもありません。章末問題の解答も少なく、演習には不適切です。中古で1円で買えますので、何かの足しに確認するくらいで良いかもしれません。
線型代数入門 (松坂和夫 数学入門シリーズ 2)
今度は、凄く丁寧に解説されている教科書です。ただ、出題可能性が低い本専攻に対してこの本を用いて別で対策するという話になると微妙です。
限られた時間、別の科目の勉強をした方が有意義な可能性が高いです。線形代数自体の勉強としてはGOODです。
解析学
書籍を購入する前に、シラバスサイトの講義ノート欄に添付されている演習問題を残さず解きましょう。その上で、下記の本を購入するか検討しましょう。
スタンダード 工学系の微分方程式 (KS理工学専門書) 広川 二郎 (著), 安岡 康一 (著)
普通です。東工大対策に特化しているわけでは無いです。もし、微分方程式に関する教科書を持っていない場合は、ご自身の所属する大学の図書館で中身を確認し、購入を検討しましょう。
他大学の微分方程式対策にも言えることですが、管理人は下記の本をオススメします。
演習 微分方程式 寺田 文行 (著), 坂田 ひろし (著)
前半の章にて、微分方程式で問われる型について網羅的に解説されています。教科書を読んで背景知識から勉強するより、都合も含め、”この解き方をすれば良い。”くらいの気持ちで勉強した方が、院試に合格する観点ではうまく行くと思います。
東工大では、変数変換などの誘導も付くことがあり、大問の最後では応用力が問われる可能性もありますが、この本をマスターしておくことで高得点が取れるはずです。
なお、積分に関しては本書に掲載されていないです。他の参考書を使用する必要があります。
新版 演習微分積分 (新版演習数学ライブラリ) 寺田 文行 (著), 坂田 ひろし (著)
大学受験でそれなりに勉強した方ならばその延長で解き方を覚えていることが多いです。演習書にて、忘れている計算テクニックを思い出す作業に終始した方が効率的だと思います。
一方で、大学に入ってから一念発起してレベルの高い大学院を受ける方もいらっしゃると思います。本音を申し上げると、細かく網羅的にマスターして欲しいところですが、時間に限りがあります。よって、上記の演習書に掲載されている例題(一変数積分、重積分の章)をマスターする方針で良いと思います。これだけならば、問題数としても大差なく、数日で終えられる分量です。
複素関数(フーリエ変換含む)
微分方程式と同じく、まずはシラバスサイトの講義ノート欄に添付されている演習問題を残さず解きましょう。その上で、下記の本を検討下さると幸いです。
電気情報数学 (電子情報工学ニューコース 15) 水本 哲弥 (著)
絶版になっているが、一応シラバスで紹介されています。説明している内容は一般的な教科書と変わりませんが、演習問題について、過去問で出題されたことのある問題が紹介されています。所属している大学の図書館にあれば、借りてみましょう。薄めの本ではありますが、1,2章のフーリエ級数、変換については必ず確認しましょう。(次点で、4章のラプラス変換)
スタンダード 工学系の複素解析 (KS理工学専門書)安岡 康一 (著), 広川 二郎 (著)
複素関数に関しては、こちらの本がシラバスで紹介されています。章末問題が略解しか無いですが、出版社HPに行くことで解答が手に入ります。ただ、自大の教科書でも問題ないと思います。
ベクトル解析
ベクトル解析のみを主眼とした難問はあまり出題されません。そのため、シラバスに掲載されている問題を解く程度で問題無いと思います。
シラバスで設定されていますが、、絶版により高いです。無理して買うほどのものでもありません。所属する大学の図書館にあれば是非借りたいですね。
演習ベクトル解析 (演習数学ライブラリ 新版 4) 寺田 文行 (著), 坂田 ひろし (著)
それでも演習したい猛者は、上記の本にて頻出問題の対策をオススメします。
他大学では、ベクトル場の回転、発散の計算は勿論、円筒/球断面のベクトル場の面積分もよく出題されます。その分の章をやっておくだけでも良いと思います。
確率統計
長くなりましたが、これで最後です。シラバスで紹介されている資料を見ての勉強で基本問題無いと思います。
それでも、別で教科書が欲しい方は、下記の本がシラバス対象になっています。(評価も良く、お勧めです。)
確率と統計: 情報学への架橋 渡辺 澄夫 (著), 村田 昇 (著)
演習書
奇抜な難問より、多くの問題を少ない時間で処理することを求められます。むやみに難しい本に手を出すべきではありませんが、下記の演習書のA問題をやっておくと良いかもしれません。
詳解と演習大学院入試問題 海老原 円 (著), 太田 雅人 (著)
一部理学部っぽい問題も混じっていますが、総じて院試で問われる数学の傾向に一番マッチしています。広く浅く演習しておいて、どの問題が出てもある程度の点が取れる知識を持っておきましょう。
対策に使える他大学の問題
基本的に、講義資料やシラバスが充実しているので他大学まで手を伸ばす必要は無いかもしれません。参考程度に頻出分野分を載せます。
- 解析学(積分):京大(先端数理)、名大、電通大、大阪公立大、広島大
- 微分方程式:阪大、名大、神戸大
- 複素関数:阪大、九大、神戸大
- フーリエ変換:東大(第3問)、阪大、東北大
全体的に、阪大がレベル的にも問題形式的にも合っていると思います。(誘導が多めですので)
フーリエ変換については、東大の第3問を確認した方が良いです。信号処理に関する分野ですが、中身はフーリエ変換の性質を説明する問題が多いです。十分、対策になると思います。
解析学(積分)については、出題する大学を取り上げたのみです。ただ積分するだけの問題が多いので、どこの大学でも大差無いと判断します。
最後に
試験問題が160分に対し、電磁気学と電気回路を合わせて3科目解く必要があります。後段の問題も計算量が多いため、数学に対して使用できる時間は50分程度(1題25分)が妥当だと思います。
数学が苦手であれば、6割でも仕方ない気持ちで解く方が、全体として見れば高得点を狙えるかもしれません。