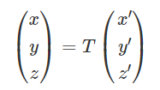東工大(東京科学大学) 情報通信系 院試の全体
数学(微分積分/線形代数)で構成されています。
試験時間は90分(9:30-11:00)です。英語はTOEICによる点数換算で、11:30-12:30の論述試験を合わせて600点満点です。
<必須科目>
- 数学(300点) ※微分積分/線形代数1問ずつ
- 論述(200点)
- 英語(100点)
なお、R4以前は、確率統計、電磁気学、電気回路、論理回路、計算機学、アルゴリズム論の出題がありました。大変広範囲です。2025年度の試験要綱次第ですが、復活の可能性は無いか注視する必要があります。
各科目の概要
数学
年によってバラツキはあるものの、微分積分の方が取りつきやすい問題が多いように考えます。複雑な式が与えられることがあるものの、大問の最初は計算して解決することが多いからです。また、極値と積分が頻出であるため、対策範囲を絞りやすいです。
線形代数は、難しいと思います。ノルムが頻出ですが、他大学ではあまり出題されないです。そのため、対策を立てづらいです。ノルムが出ない年も、階数、実対称行列の性質など、これも類題経験を積みづらいです。所謂、行基本変形をして固有値を求めて対角化をするだけで解決する問題が殆ど出ません。
まずは、微分積分を固めてから線形代数の対策をすると良いと思います。
目標
問題の難易度は高いですが、試験科目数が少ないので、6,7割目標ですね。
試験対策に役立つ記事
数学
対策に使える参考書、問題集
全体
最近5か年は以下の分野の出題がありました。
- 2023年:
- 広義積分と無限級数の和。逆関数の微分。
- 行列と正規直交基底。ノルムと残差。
- 2022年:
- ガンマ関数と積分
- 行列とノルム。固有値との関係。
- 2021年:
- 3変数関数の極値。体積の計算。
- 行列の階数(Rank)。実対称行列の証明問題
- 2020年:
- コロナにより、問題開示無し。
- 2019年:
- 変数変換を利用した2変数関数の極値
- 3次元ベクトルと正規直交基底
数学のオススメ教科書、問題集
電気電子系の記事でも同じ説明をしましたが、東工大のシラバスサイトで掲載されている資料を読み込んだ方が良いです。類題が試験に出題されることもあります。
ただ、試験難易度も高いので、さらなる高みを目指すための問題集を中心に紹介します。
微分積分
一般教養のため、開講されているクラスが多いです。そのため、情報通信系共通で使用する教科書は無いと思われます。以下は一部のクラスで使用されている教科書になります。
感想書く
多数のクラスで、昔の本を紹介していることが多いです。時間をかけて理解を深める意味では、こちらの方が良いかもしれませんが、時間に限りのある院試勉強です。私としては問題演習を多めに、下記の本での基礎勉強をオススメします。
チャート式シリーズ 大学教養 微分積分 加藤 文元 (監修)
基礎編もありますが、大学受験(一般入試)経験者ならば青い方からやった方が良いと思います。微分積分の計算自体は、大学受験で多数行うと思います。その延長線上から思い出しながらの対策をオススメします。
難問と格闘するための問題集としては、下記をオススメします。他大でも紹介していますが、A問題までの対策で良いと説明しているのに対し、本専攻を目指す際はB問題までやりこんだ方が良いと思います。
詳解と演習大学院入試問題 海老原 円 (著), 太田 雅人 (著)
解説も丁寧です。目新しい問題が多い本専攻の院試に対し、最終的に応用力(解法選択の幅)が重要になってきます。一つの問題へのアプローチの他に、どうやって考えるところから学ぶことができます。
他、時間に余裕があれば、または上記の本が難しいときは下記でも良いと思います。
微分積分: 大学院入試問題から学ぶシリーズ 池田和正 (著)
ちょっと古めの本になってきましたが、十分現代入試でも通用する内容と思います。級数、極値、積分の単元だけでも確認しましょう。
線形代数
微分積分と同様、一般教養のため、担当教員によって設定する書籍が異なります。
線型代数入門 (松坂和夫 数学入門シリーズ 2)
今度は、凄く丁寧に解説されている教科書です。
線形代数 (大学院入試問題から学ぶシリーズ) 池田和正 (著)
微分積分と同じ理由で選定しました。海老原先生の問題集が難しい場合は、こちらの購入でも良いと思います。
他、ノルムに関する問題が多いため、数値解析に関する本も目を通した方が良いかもしれません。
数値解析入門 (サイエンスライブラリ 現代数学への入門 14) 山本 哲朗 (著)
ニュートン法など、おそらく出ないと思われる単元も多いです。これらはさっと目を通すくらいで、ノルムの単元を重点的に読みましょう。(ガウスザイデル法、ヤコビ法など)
対策に使える他大学の問題
ノルムだけは、京大(先端数理)の問題に手を出してみてもよいかもしれません。専門科目の中に、数値解析の科目がありますので、その問題がオススメです。ただし、計算量に関する出題も多いため、理解を深める意味での確認程度で良いと思います。
- 微分積分:京大(先端数理、通信情報)、名大、電通大、大阪公立大、広島大
- 線形代数:京大(先端数理)、阪大、名大、東北大、北大、九大、神戸大
他、九大の線形代数も、他大学でありがちな定番問題は少ない印象です。試験勉強の休憩時間にでも、覗いてみると良いでしょう。
最後に
微分積分、線形代数ともに計算量が多く、難しい問題が続きますが、試験時間は90分あります。1題45分ありますので、大学入試を思い出して粘り強く考えることを思い出しましょう。