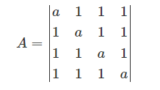東工大(東京科学大学) 情報工学系 院試の全体
数学、論理学、オートマトン、アルゴリズムとプログラミングで構成されています。
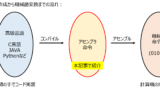
試験時間は150分(9:30-12:00)です。英語はTOEICによる点数換算で総合点の1割を占めます。
下記A~C群から各1題、合計3題選択
- A群:微分積分、線形代数、確率統計
- B群:数理論理学、オートマトンと形式言語
- C群:データ構造とアルゴリズム、プログラミング
合計900点+英語(TOEIC)100点=1000点満点
2023年度入試までは、A~C群を合わせた全体5題のうち、最初の3題を必須選択。最後の2題のうち1題のうちいずれかを選択でした。
しかし、2024年度入試から出題形式が変わったようです。勉強内容に大きな違いは出ないですが、注意が必要です。
試験傾向
全体
最近5か年は以下の分野の出題がありました。
- 2023年:
- 数学
- 実行列と行列式
- 偏微分と極値
- 確率変数と確率密度関数の計算
- 文脈自由文法と真偽判定。非決定性オートマトン。命題論理(自然演繹)。
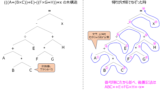
- アルゴリズムと二分探索木。要素の挿入。
- 数学
- 2022年:
- 行列の固有値と極限。行列式の計算。
- 論理関数と真理値表。選言標準形。一階述語論理。文脈自由文法の真偽判定。
- スタックの構成。キュー。動的計画法。
- 制御工学(フィードバック制御)。根軌跡。
- Dフリップフロップを用いたカウンタ。アセンブラのプログラミング。回路設計。
- 2021年:
- 3×3実行列の対角化
- 文脈自由文法と生成規則。木構造。論理式の変形。冠頭標準形。
- ヒープソートの性質。プログラムの空欄補充。
- 制御工学(PI制御。定常偏差)
- アセンブラのプログラミング。回路設計。
- 2020年:
- コロナにより、問題開示無し。
- 2019年:
- 数学:小問集合(極限の計算。行列式の計算。累積密度関数。仮説検定)
- 命題論理(自然演繹、一階述語論理)
- 各種ソートに関する問題。プログラムの空欄補充
- 制御工学(ラプラス変換の性質。微分方程式の解。力学系の伝達関数。
- 論理回路の空欄補充。回路設計。
線形代数は行列式の計算と対角化。微分積分は偏微分。確率統計は確率密度関数の計算が頻出になっています。
論理学は、自然演繹、一階述語論理に関する問題が多いです。これは、東工大色が強い内容になっています。下記に紹介する教科書を購入しての対策を推奨します。
アルゴリズム論は、ソートに関する問題が多いです。有名問題が多いため、なるべく得点源にしたいですね。
各科目の概要
A群:数学
個人的には、線形代数>微分積分>確率統計の順でオススメします。各科目間で難易度の違いはあまり無いものの、他大学を併願する上で、出題頻度の高い順から対策した方が効果が高いからです。
加えて、他の専攻と比較すると、問題自体の難易度が易しめです。他大の院試でも類題を見かけるようなものも多いので、取っつきやすい方ではあると思います。
ただし、2023年度大問1のように、微分積分と線形代数の融合問題の形式で問われることもあります。1つの科目だけ勉強していれば良いと言うわけでもないです。保険の意味も込めて、微分積分と線形代数の2科目を勉強しておくと良いです。
なお、微分積分については、他大学で頻出の極値や重積分があまり出てこない印象です。偏微分を中心に勉強しておくと良いでしょう。
B群:数理論理学、オートマトンと言語理論
科目として分かれている扱いですが、学習内容はある程度似ています。なるべく一緒に勉強した方が良いと思います。どちらかを強いて選ぶなら、オートマトンを勉強した方が、アルゴリズムなど他科目を勉強したときの親和性が高いのでオススメです。
符号の生成規則、木構造、論理式が頻出です。
論理式は2019年のような本格的な問題が出題される可能性があります。是非、東工大シラバスページで該当講義を参照して対策しましょう。
C群:アルゴリズム、プログラミング
B群と同じく、科目は分かれているものの、ほぼ同じ内容を勉強します。プログラミングをあまりしたことが無い方はアルゴリズムに重点を置いて対策した方が良いです。しかし、プログラムの空欄補充の問題が出ることもありますので、≒でプログラミングの勉強をしているのと同義です。
他、過去問を見ていると論理回路の出題がありました。B群の勉強をしていると自然と身に付くかもしれませんが、Dフリップフロップなどの基本的な内容は、念のため抑えておくようにしましょう。
その他
入試科目の再編により、2023年度までの入試(大問4)に出てくることが多かった制御工学が実質廃止になったようです。時間に余裕があれば目を通しておく程度で良いと思います。
目標
範囲は広いですが、試験問題は平易なものも多いので、7割目標にすると良いのではないかと思います。(6割だと他受験者のレベルもあって、負けてしまいそう。)
試験対策に役立つ記事
数学
情報系
試験に役立つ教科書、問題集
数学(微分積分、線形代数、確率統計)
一般教養科目のため、電気電子系、通信情報系の対策と同様です。詳しい書籍はリンク先からご覧ください。ここでは、特にオススメする問題集だけ取り上げます。
詳解と演習大学院入試問題 海老原 円 (著), 太田 雅人 (著)
他大学院と同様、本専攻においてもオススメできます。ただし、B問題までは不要かもしれません。微分積分、線形代数、確率統計ともにこの1冊で済ませられるところも良いです。
論理学の教科書
数理論理学 鹿島 亮 (著) (オススメ)
同じ大学に所属されている先生が著作していることもあり、院試の傾向と非常に合っています。演習問題も簡潔にですが解答が付いています。論理学の教科書が少ない中、本書は大変オススメです。前半の章は必ずやりましょう。
オートマトンの教科書
コンピュータサイエンスのための言語理論入門 レイワード・スミス (著), 井上 謙蔵 (監修), 吉田 敬一 (翻訳), 石丸 清登 (翻訳)
説明内容自体は丁寧にまとまっていますが、演習問題に答えが全くありません。メインで使うには厳しいです。東工大の講義資料、または上記の教科書を読んでいるうえで分からないことがあった時の副読本の位置づけで購入しても良いかもしれません。
管理人としては、下記をオススメします。
オートマトン・言語理論 [第2版] 富田 悦次 (著), 横森 貴 (著)
分かりやすい入門書です。演習問題、例題も豊富です。ただ、高得点を取るには心もとないため、過去問を通してレベルアップしましょう。
アルゴリズム
情報工学系のシラバスを見ましたが、指定教科書が見つかりませんでした。参考書には、下記が紹介されていました。
アルゴリズムイントロダクション 浅野 哲夫 (著), 岩野 和生 (著), 梅尾 博司 (著), 小山 透 (著), 山下 雅史 (著), 和田 幸一 (著)
洋書なだけあり大変分厚いです。(1100ページ弱あります。)
本書をマスターできれば、どんな問題が来ても解答できますが、読んでいるだけで院試対策シーズンが終わってしまいます。将来、アルゴリズム系の研究室に入る方以外は買わないほうが良いと思います。
もし本書を辞書的な意味で活用するときは、下記の章がオススメです。
- 2章:ソートの基本的な考え方
- 3章:計算時間、オーダー記法
- 4章:漸化式の解法
- 5章:ランダムアルゴリズム
- 6,7,8章:各種ソート(ヒープ、クイック、バケツ)
- 11章:ハッシュ法
- 12章:木構造
- 22章:幅優先選択
- 23,24章:最小全域木
- 25章:行列積
- 29章:線形計画法
- 補論B~D (集合、確率、行列の計算)
長々と書きましたが、管理人としては下記の本をオススメします。
Cによるアルゴリズムとデータ構造 茨木 俊秀 (著)
他大学の院試と傾向が変わらない問題が多いことから、変わらずオススメします。演習問題の量は少ないので、そこは過去問や他大学の院試問題で対策しましょう。
アルゴリズム論は、やみくもに問題を解くよりは理解優先で良いと思います。
プログラミング
何か本を買って勉強するより、実際に自分でコードを書いて演習することが多いです。情報工学を志望する方ならば、今までの勉強資料が残っているはずです。これを利用し、自身の知識を深めていくことをオススメします。
対策に使える他大学の問題
微分積分は極限の問題が多いので、その大学を赤字にします。線形代数はどの大学でも大差無いと考えます。論理学以降は、出題大学を並べるだけに留めます。難しめの問題を希望する際は、京大、阪大の問題をオススメします。(東大は、分量こそは多いが意外と平易な問題が多いため)
- 微分積分:京大(先端数理、通信情報)、名大、電通大、大阪公立大、広島大、岡山大
- 線形代数:京大(先端数理)、阪大、名大、東北大、北大、九大、神戸大
- 論理学:京大(通信情報)
- オートマトン:京大(通信情報)、九大
- アルゴリズム:東大、京大、阪大、東北大、九大、電通大、農工大など
最後に
学部入試と同様、院試においても本専攻は一番人気であることが予想されます。高得点が取れたからと安心せず、満点を狙うつもりで演習を重ねていきましょう。