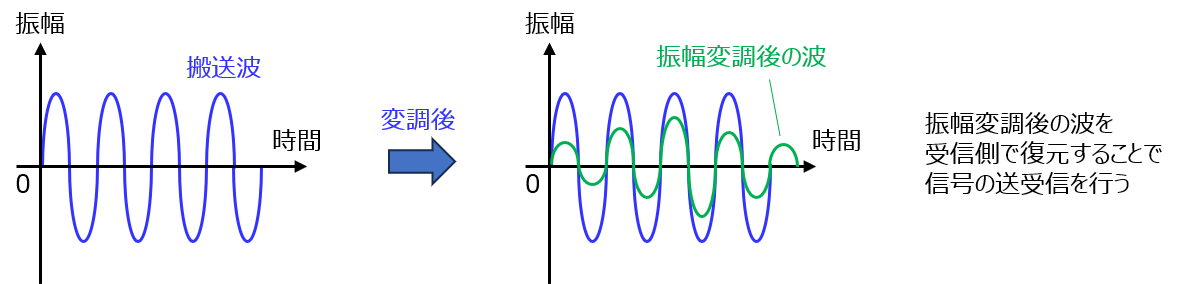
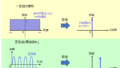
振幅A、周波数\(f_{c}\)をもつ搬送波を信号\(s(t)\)によって振幅変調した信号は
\begin{aligned}g(t)={1+m s(t)}Acos(2 \pi f_{c}t)\end{aligned}
で与えられる。ただし、\(0<m<1\)とする。以下の問いに答えよ。
(1)\(g(t)\)の周波数スペクトル\(G(f)\)を\(s(t)\)のフーリエ変換\(S(f)\)を用いて表せ。
東北大学 電気情報系院試 専門科目 2021/3 通信工学より
(2)\(S(f)\)が図1のように\(-f_{max}<f<f_{max}\)に帯域制限されたスペクトルとして与えられるとき、\(G(f)\)の概形を図示し、復調により\(s(t)\)を復元するために\(f_{c}\)が満たすべき条件を示せ。
(3)\(g(t)\)の平均電力\(P\)および電力効率\(\eta\)を\(s(t)\)の平均電力\(\bar{ s(t)^{2} }\)を用いて表せ。ただし、\(\bar s(t)=0\)であるとする。
(4)\(s(t)=\cos(2 \pi f_{s} t)\)の時の最大電力効率\(\eta_{max}\)及びその時の\(m\)の値を求めよ。ただし、\(f_{s} << f_{c}\)とする。
振幅変調(AM)とは
原理
送信したい変調信号\(s(t)\)に応じて搬送波の振幅を変化させることを言います。(AM:Amplitude Modulationの略です。)
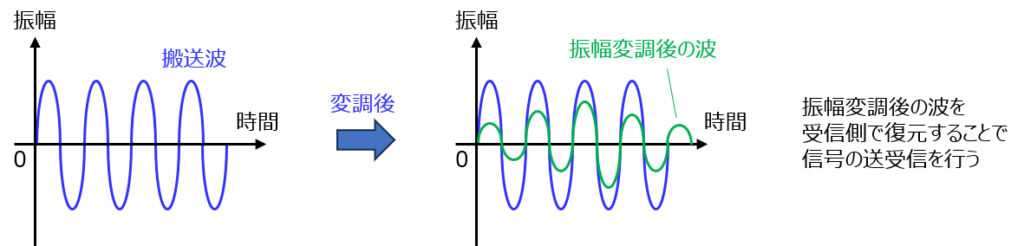
いま、上記左図のように搬送波\(A\cos(2\pi f_{c}t)\)が存在するとします。
これに対し、変調指数\(m\)をかけた変調信号\(ms(t)\)を同じ正弦波で重ね合わせると、右図のように変化します。
信号の受信側では、変調した信号の包絡線をなぞり(検波)、元の搬送波成分を打ち消すことで、変調信号を受け取ることができます。

包絡線検波が可能な条件
前節のように、変調指数\(m\)をかけた信号を搬送波に重ね合わせると、信号の送受信ができます。
変調後の信号は、(1)式で表すことができます。
よって、振幅(絶対値)の最大値は\(A(1+ms(t))\)、最小値は\(A(1-ms(t))\)になります。
仮に、\(ms(t)>1\)のとき、最小値は負の領域まで到達することになります。
負の領域にある振幅も同様に正の領域まで飛び出しますので、信号が歪みます。
こうなると、正常に包絡線を検波できなくなり、受信側で正しい信号を受信できなくなります。(過変調)
以上より、\(ms(t)≦1\)が包絡線検波が可能な条件となります。
\(s(t)=1\)のときは\(m≦1\)となり、大きくできる変調指数には限度があることが分かります。
電力効率と変調指数
搬送波に変調信号を重ね合わせた\(g(t)\)分の電力に対する変調信号\(ms(t)\)分の電力の比を電力効率と言います。
\(g(t)\)には搬送波成分も含まれますので、変調信号成分が搬送波成分に対して大きいほど電力効率が高くなると考えられます。
そのためには、変調指数\(m\)を上げることが有効だと考えられます。
しかし、前節のように高々\(m=1\)程度までしか上げられません。
実際の数値は問(4)で説明しますが、振幅変調は、他の変調方法(FM)に対して電力効率が低いです。
振幅変調のメリット、使用先
- 一つの周波数帯域で多くの情報を送受信できる
- 航空管制で使用する
- 検波回路がシンプル。(抵抗、コンデンサ、ダイオードのみで構成可)
他の変調方式(周波数変調)は、その名の通り、振幅ではなく周波数を変調します。
そのため、使用する周波数帯域が広くなる欠点があります。
また、同一の周波数の信号でFM変調波を送信する場合、一番強度の強い信号しか聞き取れないため、航空管制など、様々な相手と会話をする場面では不向きです。
一方で、振幅変調の場合、同じ周波数でも変調指数に合わせて聞き取る相手を変えられます。
他、前節で示した通り、検波回路がシンプルなので、コストを安く制作することができます。
解答例
(1)\(G(t)\)の周波数スペクトル
(1)式をフーリエ変換すると
\begin{aligned}G\left( f\right) &=\int ^{\infty }_{-\infty }\left( 1+ms(t)\right) A\dfrac{e^{-j2\pi f_{c}t}+e^{j2\pi f_{c}t}}{2}e^{-j2\pi ft}dt \\ &= \dfrac{A}{2}\int ^{\infty }_{-\infty }\left( 1+ms(t)\right) (e^{-j2\pi (f-f_{c})t}+e^{-j2\pi (f+f_{c})t}) \\ &= \dfrac{A}{2}(\delta \left( f-f_{c}\right) +\delta \left( f+f_{a}\right) +mS(f-f_{c})+mS(f+f_{c})) \end{aligned}
(2)復調可能な\(f_{c}\)の条件
(1)で求めた周波数スペクトルを図示すると、下記のようになる。
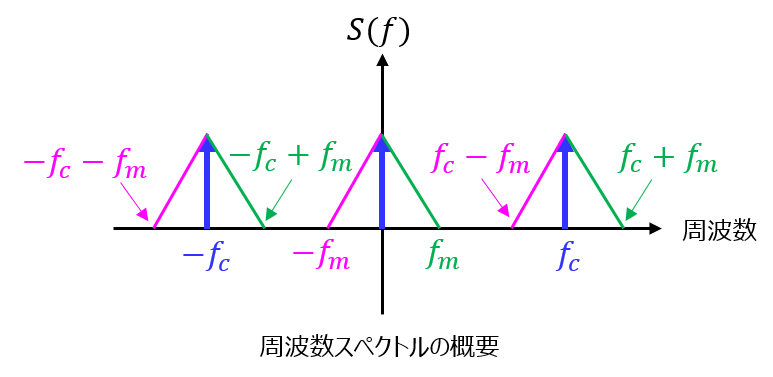
\(f_{c}\)を中心として\(±f_{m}\)分布する。
\(s(t)\)を復元するためには、左右のスペクトル同士が重ならなければ良いので
\begin{aligned}f_{c}-f_{m}>f_{m}\end{aligned}
\begin{aligned}f_{c}>2f_{m}\end{aligned}
※これをサンプリング定理と言います。振幅変調においても、必要な条件です。単に変調指数だけ気を付けていれば信号を必ず復調できるというわけではないです。
本問を教訓にしていただければと思います。
(3)平均電力と電力効率
搬送波分の平均電力\(P_{1}\)と変調信号分の平均電力\(P_{2}\)を分けて考える。
搬送波成分について、\(A\cos(2 \pi f_{c}t)\)だから、実効値を取り
\begin{aligned}P_{1}=\dfrac{A^{2}}{2}\end{aligned}
変調信号成分について、\(ms(t)A\cos(2 \pi f_{c}t)\)だから、同じ計算をして
\begin{aligned}P_{2}=m^{2}\bar{ s(t)^{2} }\dfrac{A^{2}}{2}\end{aligned}
これより、\(g(t)\)の平均電力\(P\)は、\(P=P_{1}+P_{2}\)
求める電力効率\(\eta\)は
\begin{aligned}\eta&=\dfrac{P_{2}}{P_{1}+P_{2}} \\ &=\dfrac{m^{2} \bar{ s(t)^{2} }}{1+m^{2}\bar{ s(t)^{2} }}\end{aligned}
(4)最大電力効率
\(s(t)=cos(2\pi f_{s}t)\)とすると、\(\bar{ s(t)^{2} }=\frac{1}{2}\)。
よって、(7)式は
\begin{aligned}\eta &= \dfrac{\frac{m^{2}}{2}}{1+\frac{m^{2}}{2}} \\ &=\dfrac{1}{1+\frac{2}{m^{2}}}\end{aligned}
できるだけ分母を小さくするほど電力効率が高い。
\(0≦m≦1\)より、\(m=1\)のとき、最大電力効率\(\eta=1/3\)が得られる。
振幅変調の最大電力効率は高々33.3%であることが分かりました。
3分の2は搬送波成分で消費され、信号の送受信に意味を成しません。
最後に
通信方式は、東大(第3問)や京大(通信情報)にて出題されることがあります。
本問は、振幅変調に関する基本的な考え方が詰まっています。
両大学を志望される方は、是非チェックすると良いです。