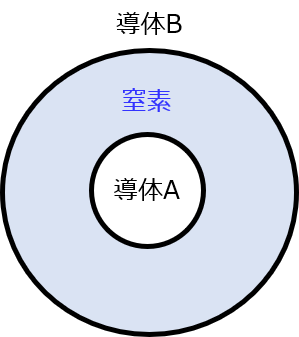
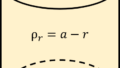下記の図のように、導体A,B間に絶縁材料(窒素ガス)を詰めた同軸ケーブルを考える。
(1) 窒素ガス中の放電において、電子の平均速度を\(v_{e}\)、電子と窒素分子の密度をそれぞれ\(n_{e}、n_{g}\)、電子と窒素分子の衝突断面積を\(\sigma\)とする。このとき、下記の文章の(i)～(iii)の関係式を完成させよ。ただし、窒素分子の平均速度は\(v_{e}\)より十分小さいとする。
「電子の平均自由行程\(\lambda_{e}\)と電子の窒素分子に対する衝突周波数\(f_{e}\)の間には、(i)の関係式が成立する。また、\(f_{e}\)と\(n_{g}\)の間には(ii)の関係式がある。よって、\(\lambda_{e}\)と\(n_{g}\)の間には\(\lambda_{e}\)と\(n_{g}\)の関係は(iii)で表される。
(2)窒素ガスの圧力を大気圧から大幅に増加させると、導体AB間の絶縁破壊電圧は増加した。また、圧力を大気圧から大幅に減少させた場合も、絶縁破壊電圧は増加した。それぞれの理由を説明せよ。
東大 電気系工学専攻 大学院入試 2014 問題F (4),(5)より引用
はじめに
またまた、院試問題を考察します。カテゴリーとしては電力系統工学ですが、実際の分野は高電圧工学かもしれません。
電力系統工学でありがちな地絡などの回路計算は、他サイト様が充実しています。新規性のある記事を作成する。という観点では、知っていると少しオトクになりそうな記事を紹介することが一番と考えています。ですので、本分野の一番目の記事として、絶縁破壊を紹介します。
電験では、電気材料の分野に分類されます。送電線の種類にGILがあります。GILは、(Gas insulated transmission line)の略であり、六フッ化硫黄を充填した管路内に送電ケーブルを入れる方式です。SF6は、化学的に安定で高い絶縁性を持つため使用されています。しかし、なぜ大気圧より高い圧力で充填しているのか、細かく述べられていることが少ないように感じます。
そこで、本記事では、ケーブルの周りに気体を使用した時、圧力変化が絶縁性にどう効いてくるのかを考察したいと思います。
絶縁破壊の原理
電子と分子が衝突することで発生する「電離」がキーワードになります。
電離とは
原子の周りに存在する軌道上には電子があります。十分に加速したエネルギーを持つ電子が原子(分子)と衝突すると、非弾性衝突により、エネルギー損失が発生します。
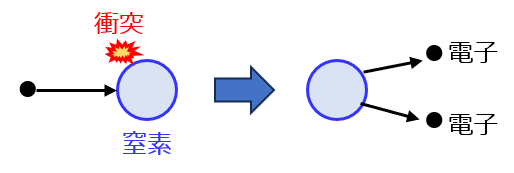
このエネルギーを受け取り、電子が原子の軌道上から離脱することがあり、これを電離と言います。
電離が繰り返されると
電離が発生すると、その分だけ電子の分離が発生し、電場が大きくなります。
電場が大きくなると、電極間の電位差が大きくなります。
その結果、ある電場を超えると電極間の絶縁が破壊され、電荷が移動するようになります。
これを絶縁破壊と言い、本問を解答するうえで重要な考え方となります。
解答例
(1) (i)～(iii) 電子の平均自由行程と窒素ガス密度の関係
簡単化のため、下記のような模式図を考えます。衝突周波数\(f_{e}\)とは、電子と窒素分子が1秒間に衝突する回数です。これは、電子の速度\(v_{e}\)に平均自由行程\(\lambda_{e}\)を割ることで表現できます。
\begin{eqnarray}f_{e}=\dfrac{v_{e}}{\lambda_{e}}\end{eqnarray}
上式を変形することで、(i) \(\lambda_{e}=\dfrac{v_{e}}{f_{e}}\)になります。
続いて、(ii)です。衝突周波数\(f_{e}\)を考えます。
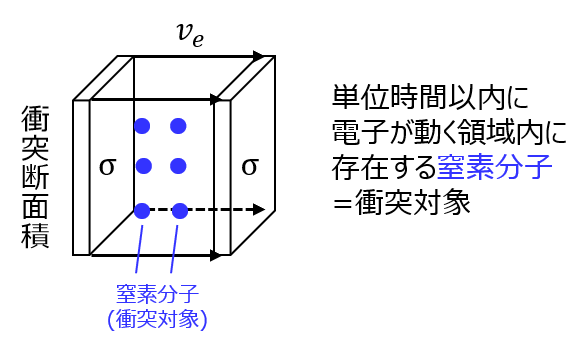
単位時間あたりに電子が移動する距離は\(v_{e}\)で、衝突断面積は\(\sigma\)です。
よって、体積\(V=v_{e}\sigma\)の領域に窒素分子が存在する場合、衝突すると考えられます。
窒素分子の密度は\(n_{g}\)のため、これを掛け合わせることで衝突周波数\(f_{e}\)の関係式を導くことができます。
(ii)の解答例： \(f_{e}=n_{g}v_{e}\sigma\)
(iii)は、(ii)の結果を(i)に代入すれば良く\(\lambda_{e}=\dfrac{1}{n_{g}\sigma}\)になります。
(iii)の結果から、窒素の密度が高いとき、電子はすぐに衝突するため、平均自由行程が小さいことが分かりました。
(2) 窒素ガス圧力と絶縁破壊電圧の関係
こちらが本記事のメイントピックです。
(1)の結果も参考に、理由を説明していくことになります。
まず、圧力を増加させた場合です。(1)の最後の考察が役立ちます。
窒素密度が大きくなるので、電子の平均自由行程が小さくなります。これにより、電子が十分に加速しないまま窒素分子と衝突します。電離に必要な運動エネルギーを持っていないため、電離は発生しません。この結果、絶縁破壊電圧は大きくなります。
次に、圧力を減少させた場合です。こちらは、そもそもの電離の発生要因から考察します。
電離するためには、窒素分子と衝突する必要があります。しかし、窒素密度が小さくなることで、衝突する機会が生まれなくなります。その結果、真空に近い場合でも、絶縁破壊電圧は大きくなります。
パッシェンの法則
上記の考察は、パッシェンの法則により表されます。
平板間の期待の圧力をp、平行平板間の距離をdとし、積をx軸にプロットします。
絶縁破壊し、火花放電開始する電圧を\(V_{s}\)とすると、下記の図で表せます。
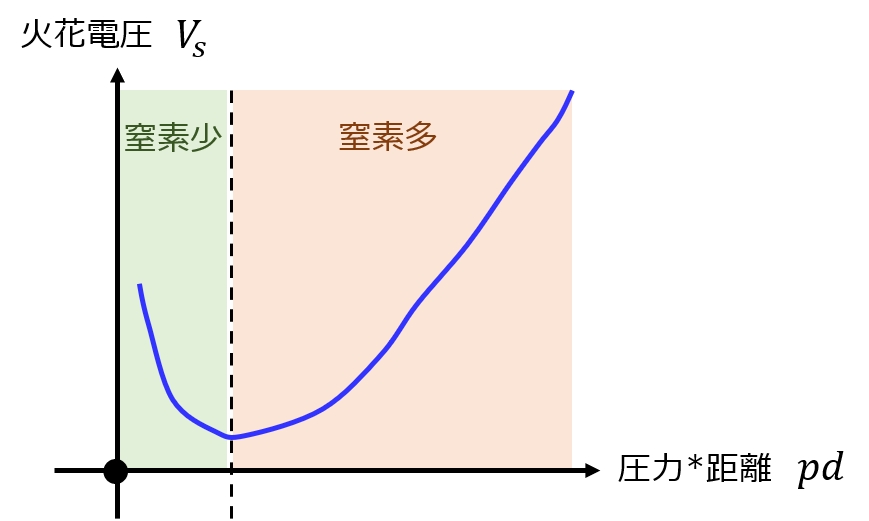
pdが大きいときは、標記の問題(2)の窒素分子の圧力が大きいときを意味しています。
pdが小さいときは、窒素分子の圧力が小さい時を意味しています。
前章で行った考察は、実際に法則として立証されていることが分かりました。
補足
本問で議論した絶縁破壊に関するメカニズムは、あくまでも絶縁体が理想的である場合の話です。実際は、ケーブル管路内に水分が入るなどし、局所的に絶縁率が低下することがあります。(水トリー)
ケーブル設計をする際は、劣化による絶縁性の低下も考える必要があります。
最後に
電気材料は、電気主任技術者試験の電力分野で毎年1問程度出題される分野です。基本的に一次試験のマーク式で出題されることが多いので、ここまでの理解は不要かもしれません。
2次試験の論述を行う際に予備知識として持っておくと役立つかもしれません。余力があれば覚えておくと良いかと思います。
参考文献
高電圧工学[第2版]：日髙 邦彦(著) 第3章
