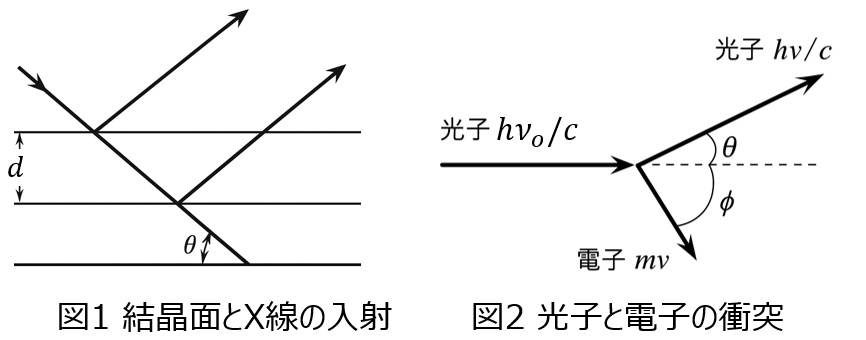
問1:図1のように、波長$\lambda$のX線が結晶面に対し角度$\theta$で入射する系を考える。結晶面の間隔を$d$とするとき、強い反射波の得られる条件を求めよ。
問2:図2のように、エネルギー$E_{o}$のX線が静止している電子と衝突する系を考える。散乱後のX線のエネルギー$\varepsilon$を求めよ。ただし、入射光子、散乱光子の振動数をそれぞれ$\nu_0, \nu$、散乱光子、電子の射出角をそれぞれ $\theta, \phi$、電子の速度を$v$、光速を$c$とし、$\beta = v/c$ とおくこと。
ブラッグ反射とは
結晶格子によって、X線などの波が強め合う現象を言います。問題で示した図1のように、結晶中の原子は規則正しく並んでおり、これを結晶面とみなせます。
波が結晶に入射すると、各格子面で波が散乱され、ある特定の入射角において隣接する格子面からの散乱波が強め合うときにブラッグ反射は発生します。
隣接する格子面との距離を$d$とし、散乱角を$\theta$とすると、下記式で表されます。
\begin{aligned}n \lambda=2d \sin \theta\end{aligned}
なお、$n$は自然数で、詳しい導出は問1で行います。
ブラッグ反射の性質
- 選択的反射:ある特定の角度でのみ強い反射が発生する
- 波長依存性:波長$\lambda$が短いほど、高次のブラッグ反射が計測可能になること
- 格子面間隔$d$の算出:実験的に$\theta$を求めることで、$d$も間接的に分かる
どれも、(1)式の性質から説明が付きます。波長依存性については、波長が短いほど、nを大きくすることができ、ある程度の$\theta$が確保でき、計測可能になります。
上記の性質により、結晶構造解析、薄膜評価に用いられています。
コンプトン散乱とは
高エネルギー光子が電子と衝突すると、光子が持つ一部のエネルギーは電子に与えられます。その結果光子は一部のエネルギーを失い波長が長くなり、電子は運動エネルギーを得て反跳(エネルギー変換)する現象を言います。
散乱前の光子の波長を$\lambda$、散乱後の波長を$\lambda^{\prime}$、散乱角を$\theta$、$m_{e}$を電子の質量とすると下記の関係になります。
\begin{aligned}\lambda^{\prime}-\lambda=\dfrac{h}{m_{e}c}(1-\cos \theta)\end{aligned}
詳細な導出は問2で行います。
コンプトン散乱の性質
- エネルギー損失:散乱した光子の波長は必ず長くなる
- 散乱角による波長の変動依存性:$\theta=\pi$で最大変動する
- 光が粒子である根拠:電子と運動量をやり取りする現象であるため
試験で問われることは少ないですが、技術者として生きていく上で必要な知識です。一般教養として覚えておきましょう。
ブラッグ反射とコンプトン散乱から分かること
どちらも光と物質の相互作用を表していますが、ブラッグ反射には波の干渉が発生していることから、光には波動の性質を持つことが分かります。一方で、コンプトン散乱では衝突が発生していることから、光は粒子である性質も持ち合わせていることが分かります。
二つの現象は、光の二重性を補完して説明しています。
解答例
問1:ブラッグ反射条件
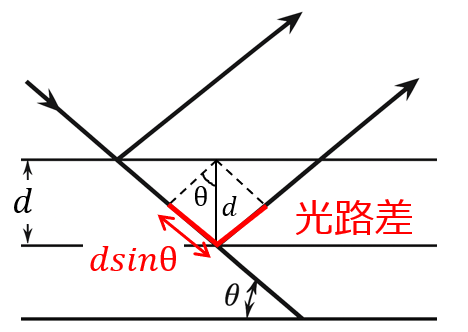
光路差は赤線部になる。一辺$d\sin \theta$で表され、入射分と反射分を考えるため
\begin{aligned}2d \sin \theta=n \lambda\end{aligned}
ただし、$n$は整数である。
問2:散乱後のエネルギー
エネルギー保存則より
\begin{equation}
h\nu_0 + m_0c^2 = h\nu + \frac{m_0c^2}{\sqrt{1-\beta^2}}
\tag{1}
\end{equation}
運動量保存則より、
\begin{equation}
\frac{h\nu_0}{c} = \frac{h\nu}{c}\cos \theta + \frac{m_0 v}{\sqrt{1-\beta^2}} \cos \phi
\tag{2}
\end{equation}
\begin{equation}
0 = \frac{h\nu}{c} \sin \theta – \frac{m_0 v}{\sqrt{1-\beta^2}} \sin \phi
\tag{3}
\end{equation}
入射光子、散乱光子の波長をそれぞれ $\lambda_0 = c/\nu_0, \, \lambda = c/\nu$ とおいて、(2), (3)式の$\phi$を を消去すれば、
\begin{align}
\left( \frac{h\nu_0}{c} – \frac{h\nu}{c}\cos \theta \right)^2+\left( \frac{h\nu}{c} \right)^2 \sin^2 \theta
&= \left( \frac{m_0 v}{\sqrt{1-\beta^2}} \right)^2
\end{align}
\begin{aligned}\left( \frac{h}{\lambda_0} – \frac{h}{\lambda}\cos \theta \right)^2+\left( \frac{h}{\lambda} \right)^2 \sin^2 \theta
&= \frac{m_0^2 v^2}{1-\beta^2}\end{aligned}
$v=\beta c$を用いると
\begin{aligned}\left( \frac{h}{\lambda_0} – \frac{h}{\lambda}\cos \theta \right)^2+\left( \frac{h}{\lambda} \right)^2 \sin^2 \theta= \frac{m_0^2 c^2}{1-\beta^2} – m_0^2 c^2\end{aligned}
(1) を変形すれば、
\begin{equation}
(h\nu_0 – h\nu + m_0 c^2)^2 = \frac{m_0^2 c^4}{1-\beta^2}
\end{equation}
\begin{aligned}
\left( \frac{h}{\lambda_0} – \frac{h}{\lambda} + m_0 c \right)^2
= \frac{m_0^2 c^2}{1-\beta^2}
\end{aligned}
(6)、(8)式から $\beta^2$ を消去して整理すれば、
\begin{aligned}\left( \frac{h}{\lambda_0} – \frac{h}{\lambda}\cos \theta \right)^2+\left( \frac{h}{\lambda} \right)^2 \sin^2 \theta
= \left( \frac{h}{\lambda_0} – \frac{h}{\lambda} + m_0 c \right)^2 – m_0^2 c^2\end{aligned}
\begin{aligned}\quad \lambda = \lambda_0 + \frac{h}{m_0 c}(1 – \cos \theta)
\end{aligned}
$\varepsilon’=h \nu=\frac{hc}{\lambda}$を用いて上式を振動数表示に変換する。逆数を取って
\begin{aligned}\dfrac{1}{\lambda}=\dfrac{1}{\lambda_0 + \frac{h}{m_0 c}(1 – \cos \theta)}\end{aligned}
$\varepsilon’=h \nu=\dfrac{hc}{\lambda},\varepsilon=\dfrac{hc}{\lambda_o}$を代入すると
\begin{aligned}\dfrac{\varepsilon’}{hc}=\dfrac{1}{\frac{hc}{\varepsilon_o}+\frac{h}{m_o c^{2}}(1-\cos \theta)}\end{aligned}
\begin{aligned}\varepsilon’&=\dfrac{hc}{h\left(\frac{c}{\varepsilon}+\frac{1}{m_{o} c}(1- \cos \theta)\right)} \\ &=\dfrac{1}{\frac{1}{\varepsilon}+\frac{1- \cos \theta}{mc^{2}}}\end{aligned}
\begin{aligned}\varepsilon’ = \frac{\varepsilon}{1 + \dfrac{\varepsilon}{m_0 c^2}(1 – \cos \theta)}
\end{aligned}