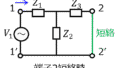
下記の理想変成器結合回路のF行列を求めよ。
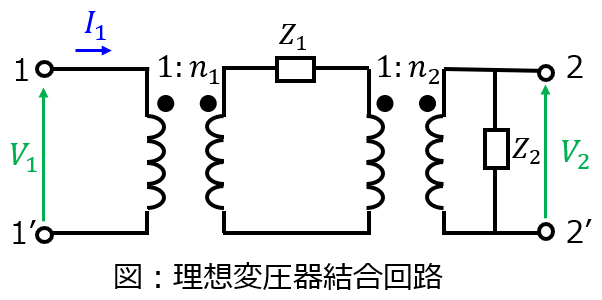
F行列とは
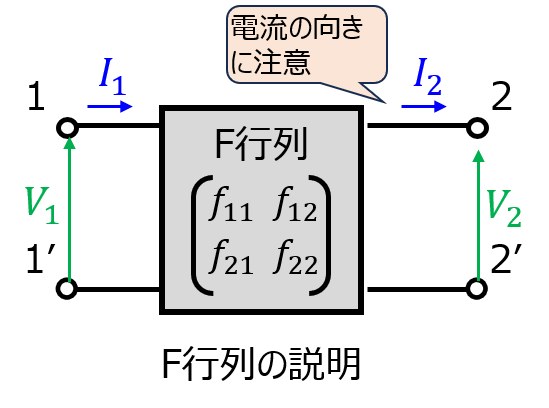
二端子対回路の一方の端子で発生する電圧\(V_{1}\)、電流\(I_{1}\)をもう一方の端子で発生する電圧\(V_{2},I_{2}\)を用いて下記で表したものになります。(継続行列(K行列)、伝送行列とも呼びます。)
\begin{aligned}\begin{pmatrix} V_{1} \\ I_{1} \end{pmatrix}=\begin{pmatrix} f_{11} & f_{12} \\ f_{21} & f_{22}\end{pmatrix}\begin{pmatrix} V_{2} \\ I_{2} \end{pmatrix}\end{aligned}
左辺は\(V_{1},I_{1}\)で表されています。右辺の未知数\(V_{2},I_{2}\)が求まれば、比を取ることでインピーダンス\(Z_{1}\)を簡単に求めることができます。
F行列は(Fundamental matrix)の略です。上記の利点から、昔は電気回路を解くために盛んに使われていました。このため、”Fundamental”(基本的)という呼び名となっています。
F行列を求めるための操作
電圧源\(V_{1}\)を接続している状態で下記操作を実施する。
- 端子2を開放\(V_{2}=0\)し、\(V_{1},I_{1},I_{2}\)の関係式を求める。
- 端子2を短絡\(I_{2}=0\)し、電流\(I_{1},I_{2}\)の関係式を求める。
- 1.2.で求めた関係式を用い、F行列の具体的な値を求める。
Z行列、Y行列は、端子1-1’も開放したり、短絡したりしましたが、F行列に関しては端子2-2’のみ対応します。(1)式の右辺のパラメータに\(V_{2},I_{2}\)がありますが、それぞれに0を代入し、パラメータを求めやすくする。ということですね。
なお、電流\(I_{2}\)の向きは回路から離れる方向を正と置きます。これは、Z行列、Y行列と逆です。注意しましょう。
例題
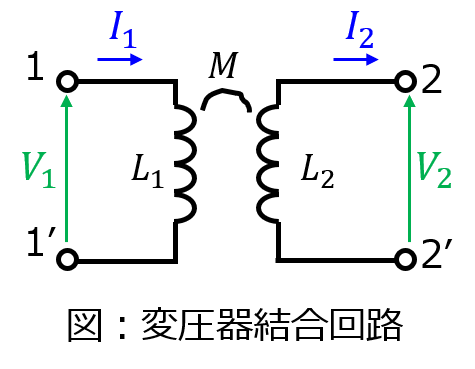
上記の変圧器結合回路のF行列を考えます。回路方程式は
\begin{cases}V_{1}=j \omega L_{1}I_{1}-j \omega M I_{2} \\ V_{2}=j \omega M I_{1}-j \omega L_{2}I_{2}\end{cases}
第2式を変形すると
\begin{aligned}I_{1}=\dfrac{1}{j \omega M}V_{2}+\dfrac{L_{2}}{M}I_{2}\end{aligned}
これが\(f_{21},f_{22}\)成分に対応する。
(3)式を(2)の第一式に代入すると
\begin{aligned}V_{1}&=j \omega L_{1}\left(\dfrac{V_{2}}{j \omega M}+\dfrac{L_{2}}{M}I_{2}\right)-j \omega M I_{2} \\ &=\dfrac{L_{1}}{M}V_{2}+j \omega \dfrac{L_{1}L_{2}}{M}I_{2}-j \omega MI_{2}\end{aligned}
これが\(f_{11},f_{12}\)に対応する。以上より、求めるF行列は
\begin{pmatrix} \dfrac{L_{1}}{M} & j \omega \dfrac{L_{1}L_{2}}{M}-j \omega M \\ \dfrac{1}{j \omega M} & \dfrac{L_{2}}{M} \end{pmatrix}
F行列の性質
行列\(\begin{pmatrix} f_{11} & f_{12} \\ f_{21} & f_{22}\end{pmatrix}\)について
- 相反定理が成立するとき、\(f_{11}f_{22}-f_{12}f_{21}=1\)
- F行列が\(\boldsymbol{F_{1}},\boldsymbol{F_{2}}\)で表される回路を左から順に直列で接続した時、回路全体のF行列は\(\boldsymbol{F_{1}}\boldsymbol{F_{2}}\)
1.について、一応紹介しました。ざっくり申し上げて、端子1-1′,2-2’どちらから見ても回路が対称のときに成立します。ただ、問題を解くうえでは補助的なものになります。前節で申し上げた手順に則って解いた方が早いです。検算程度に使えます。
2.について、Z行列、Y行列がそうであったように、F行列においても既知の行列の組み合わせで回路全体のF行列を表現できます。
ただし、Z行列、Y行列は、足し算で表現できたのに対し、F行列は積で考えます。ここだけは混同しないようにしましょう。
解答例
理想変成器結合回路のF行列
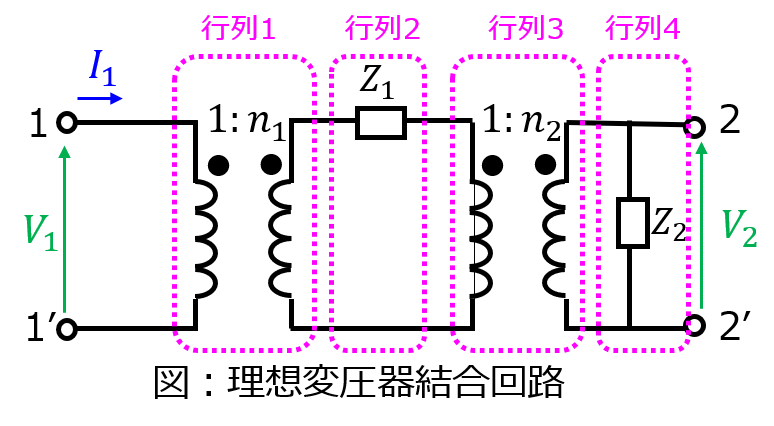
回路は下記の素子4つで構成されている。
- 巻き数比\(1:n_{1}\)の理想変成器
- 端子間に直列で接続されたインピーダンス\(Z_{1}\)
- 巻き数比\(1:n_{2}\)の理想変成器
- 端子2-2’間に接続されたインピーダンス\(Z_{2}\)
上から順に、F行列を\(\boldsymbol{F_{1}},\boldsymbol{F_{2}},\boldsymbol{F_{3}},\boldsymbol{F_{4}}\)とする。
このとき、F行列の性質2.により、回路全体のF行列\(\boldsymbol{F}\)は
\begin{aligned}\boldsymbol{F}=\boldsymbol{F_{1}}\boldsymbol{F_{2}}\boldsymbol{F_{3}}\boldsymbol{F_{4}}\end{aligned}
で表される。よって、1~4の行列を個々に求めていけば良い。
行列\(\boldsymbol{F_{1}},\boldsymbol{F_{3}}\)
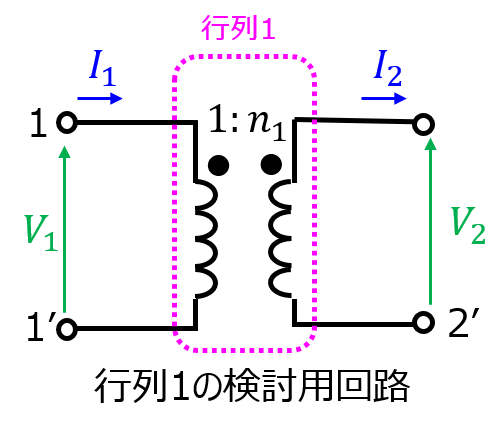
まず、行列\(\boldsymbol{F_{1}}\)について、回路方程式を考える。
\begin{cases}I_{1}=nI_{2} \\ V_{2}=nV_{1}\end{cases}
これを(1)式と比較すると、
\begin{aligned}\boldsymbol{F_{1}}=\begin{pmatrix}1/n_{1} & 0 \\ 0 & n_{1}\end{pmatrix}\end{aligned}
行列\(\boldsymbol{F_{3}}\)も同じ形状をしているので
\begin{aligned}\boldsymbol{F_{3}}=\begin{pmatrix}1/n_{2} & 0 \\ 0 & n_{2}\end{pmatrix}\end{aligned}
行列\(\boldsymbol{F_{2}}\)
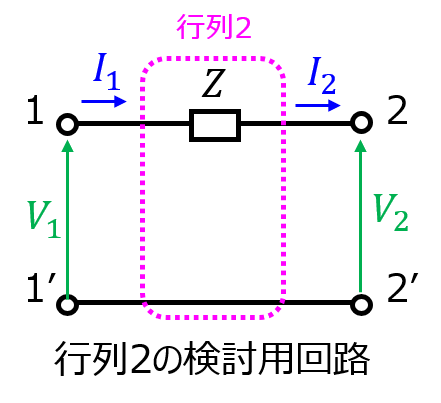
回路方程式は下記で表される。
\begin{cases}V_{1}=V_{2}+nI_{1} \\ I_{1}=I_{2}\end{cases}
以上より、F行列は
\begin{aligned}\boldsymbol{F_{2}}=\begin{pmatrix}1 & Z_{1} \\ 0 & 1\end{pmatrix}\end{aligned}
行列\(\boldsymbol{F_{4}}\)
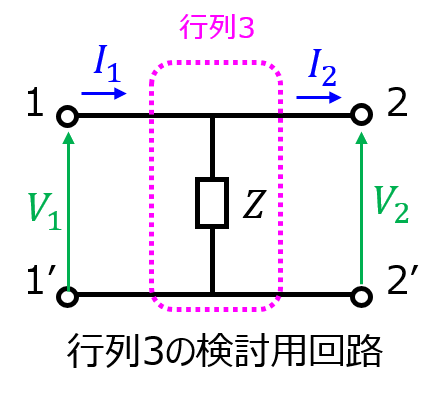
同じく、回路方程式は
\begin{cases}V_{1}=V_{2} \\ I_{1}=\dfrac{V_{2}}{Z_{2}}+I_{2}\end{cases}
以上より、F行列は
\begin{aligned}\boldsymbol{F_{4}}=\begin{pmatrix}1 & 0 \\ 1/Z_{1} & 1\end{pmatrix}\end{aligned}
回路全体のF行列
(8)(9)(11)(13)式を(6)式に代入すると
\begin{aligned}\boldsymbol{F} & =\begin{pmatrix}1/n_{1} & 0 \\ 0 & n_{1}\end{pmatrix}\begin{pmatrix}1 & Z_{1} \\ 0 & 1\end{pmatrix}\begin{pmatrix}1/n_{2} & 0 \\ 0 & n_{2}\end{pmatrix}\begin{pmatrix}1 & 0 \\ 1/Z_{1} & 1 \end{pmatrix} \\ &= \begin{pmatrix}\dfrac{1}{n_{1}n_{2}}+\dfrac{n_{2}Z_{1}}{n_{1}Z_{2}} & \dfrac{n_{2}Z_{1}}{n_{1}} \\ \dfrac{n_{1}n_{2}}{Z_{2}} & n_{1}n_{2}\end{pmatrix}\end{aligned}
最後に
Z行列、Y行列など紹介してきましたが、院試で最も出やすいのはF行列になります。最優先で対策しましょう。