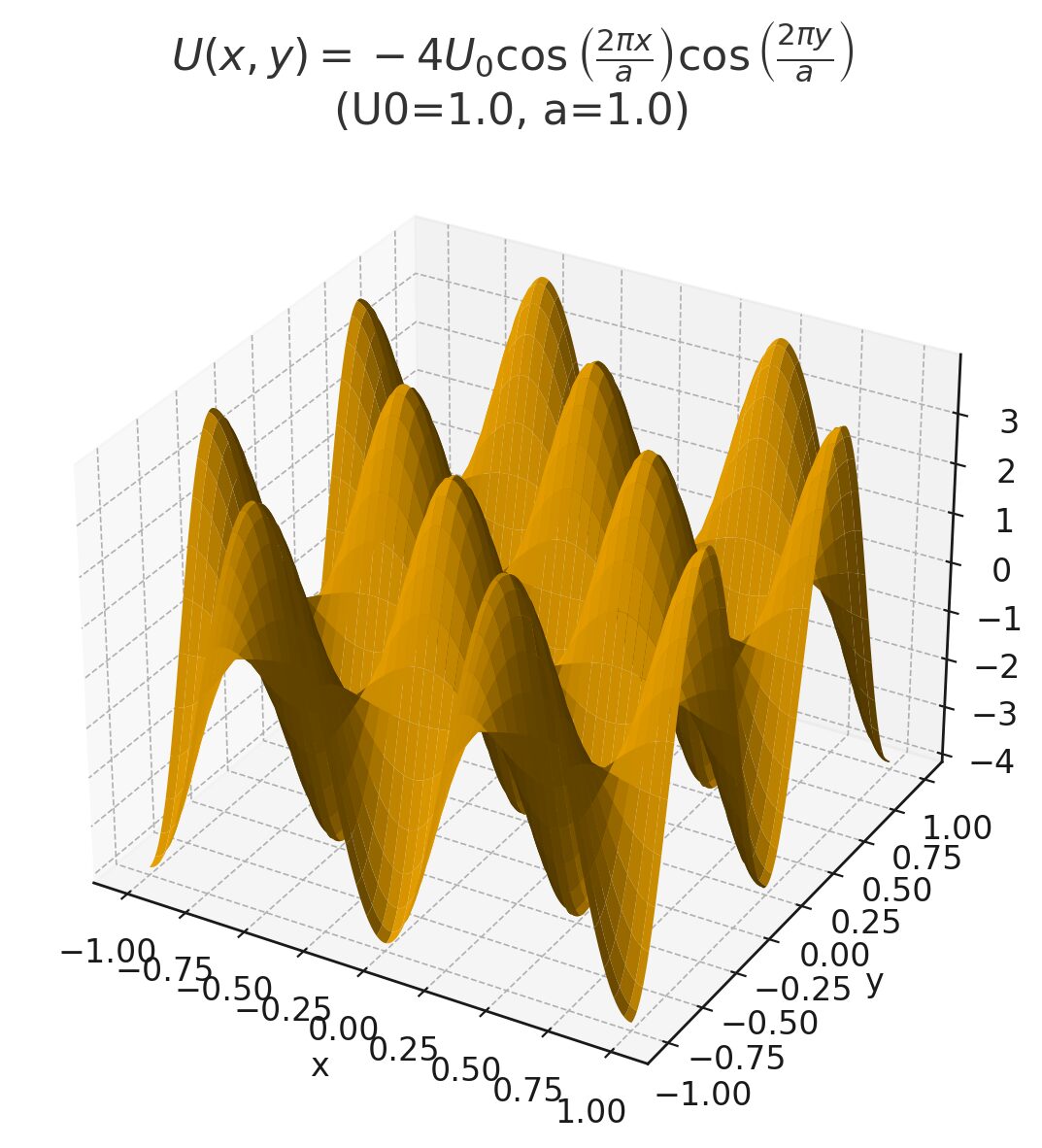
下記のような2次元の結晶ポテンシャルを考える。点(π/a,π/a)におけるエネルギーギャップを求めよ。
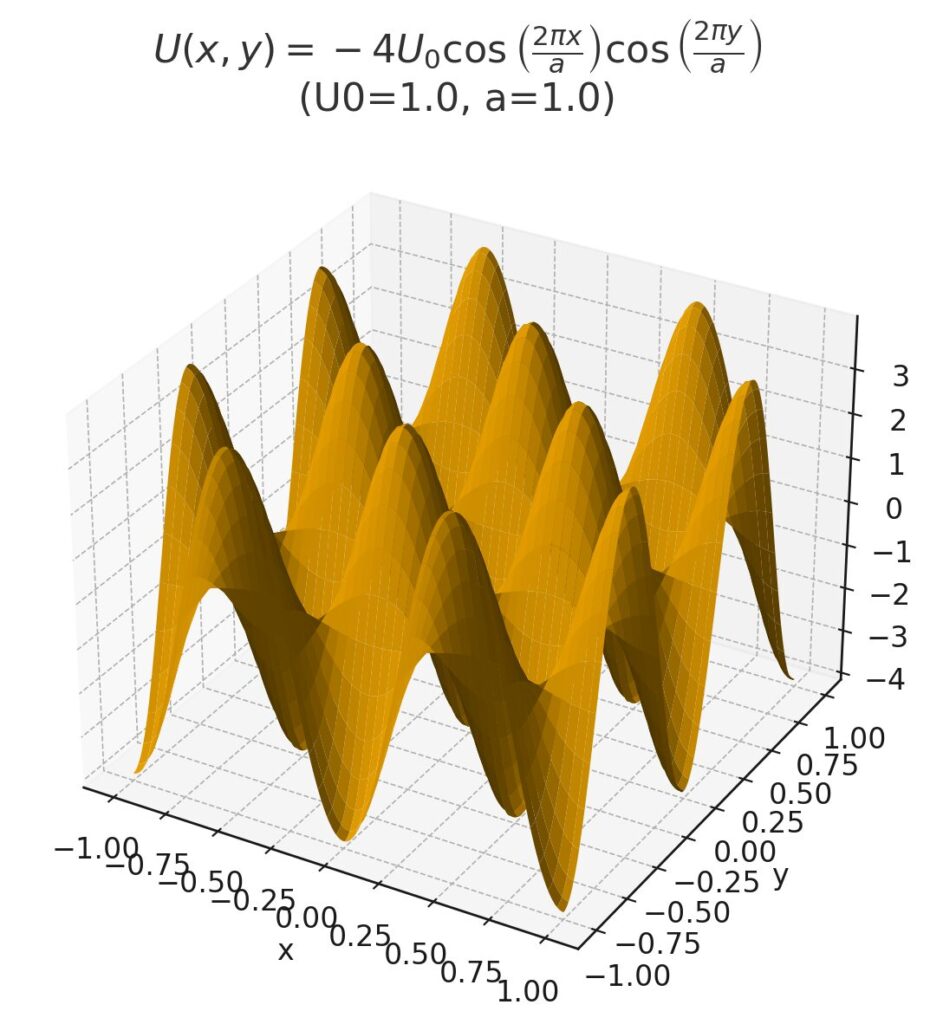
\begin{aligned}U(x,y)=-4U_{o}\cos\left(\dfrac{2 \pi x}{a}\right)\cos\left (\dfrac{2 \pi y}{a}\right)\end{aligned}
ブロッホの定理とは
周期$\boldsymbol{T}$を持つポテンシャル内の波動関数$\psi(\boldsymbol{r})$は下記のように記載可能なルールを言います。$u(\boldsymbol{r})$は結晶と同じ周期性を持つ関数とすると、下記の関係になります。
\begin{cases}\psi(\boldsymbol{r})=e^{i \boldsymbol{k} ・\boldsymbol{r}}u(\boldsymbol{r}) \\ u(\boldsymbol{r}+\boldsymbol{T})=u(\boldsymbol{r})\end{cases}
つまり、周期ポテンシャル内のある地点$\boldsymbol{r}$の波動関数は、周期$\boldsymbol{T}$足した地点での波動関数とも等しいことを示しています。本問では、ポテンシャル関数の三角関数項を$\exp$項に分解し、本定理の適用を考えます。
なお、位置ベクトル$\boldsymbol{r}$で説明をしましたが、結晶中の波の場合、逆格子ベクトル$\boldsymbol{G}$を用いると、下記の関係でも表されます。
\begin{aligned}e^{i(\boldsymbol{k}+\boldsymbol{G})・\boldsymbol{r}}=e^{i \boldsymbol{k}・\boldsymbol{r}}\end{aligned}
解答例
与えられたポテンシャルは下記のように変形できる。
\begin{aligned}
U(x,y))&=-4U_{o}\cos\left(\frac{2 \pi x}{a}\right)\cos\left (\frac{2 \pi y}{a}\right)\\ &=-U_{o}\left \lbrace \exp \left(i \frac{2 \pi(x+y)}{a}\right) +\exp \left(-i \frac{2 \pi(x+y)}{a}\right) \right. \\
&\left. +\exp \left(i \frac{2 \pi(x-y)}{a}\right)+\exp \left(-i \frac{2 \pi(x-y)}{a}\right) \right \rbrace
\end{aligned}
定数$C(k)$を考え、波動関数$\psi(k)$を下記のように置く。逆格子ベクトルを$\boldsymbol{G}$と置き、原点(0,0)を結晶格子の中心とすると、$±\frac{1}{2}G=(±\frac{\pi}{a},±\frac{\pi}{a})$で一周期になる。ブロッホの定理より
\begin{aligned}U(\boldsymbol{r})=\sum_{G}U_{G} \exp(i \boldsymbol{G}・\boldsymbol{r})\\ \psi(k)=\sum_{k}C(k)\exp(i \boldsymbol{k}・\boldsymbol{r})\end{aligned}
をシュレーディンガー方程式に代入して
\begin{aligned}\left\lbrack -\frac{\hbar^2}{2m} \nabla^2 + U(\mathbf{r}) \right\rbrack \psi(\mathbf{r}) = \varepsilon \psi(\mathbf{r})\end{aligned}
\begin{aligned}(\lambda-\varepsilon)C(k)+\sum_{G}U_{G}C(k-G)=0\end{aligned}
\begin{cases}(\lambda – \varepsilon)C(\frac{1}{2}G)-U_{o}C(-\frac{1}{2}G)=0 \\ -U_{o}C(\frac{1}{2}G)+(\lambda – \varepsilon)C(-\frac{1}{2}G)=0 \end{cases}
ただし、$\varepsilon$はエネルギー固有値で、$\lambda=\frac{\hbar^{2}k^{2}}{2m}$である。
$C(\frac{1}{2}G)=C(-\frac{1}{2}G)=0$以外の解を持つためには、係数に関わる行列式が0になれば良い。
\begin{aligned}\begin{vmatrix}\lambda -\varepsilon & -U_{o} \\ -U_{o} & \lambda-\varepsilon\end{vmatrix}=0\end{aligned}
\begin{aligned}(\lambda-\varepsilon)^{2}-U_{o}^{2}=0\end{aligned}
$\lambda=\varepsilon ± U_{o}$で、二つの$\lambda$の差は$2U_{o}$。よって求めるエネルギーギャップは$2U_{o}$
補足
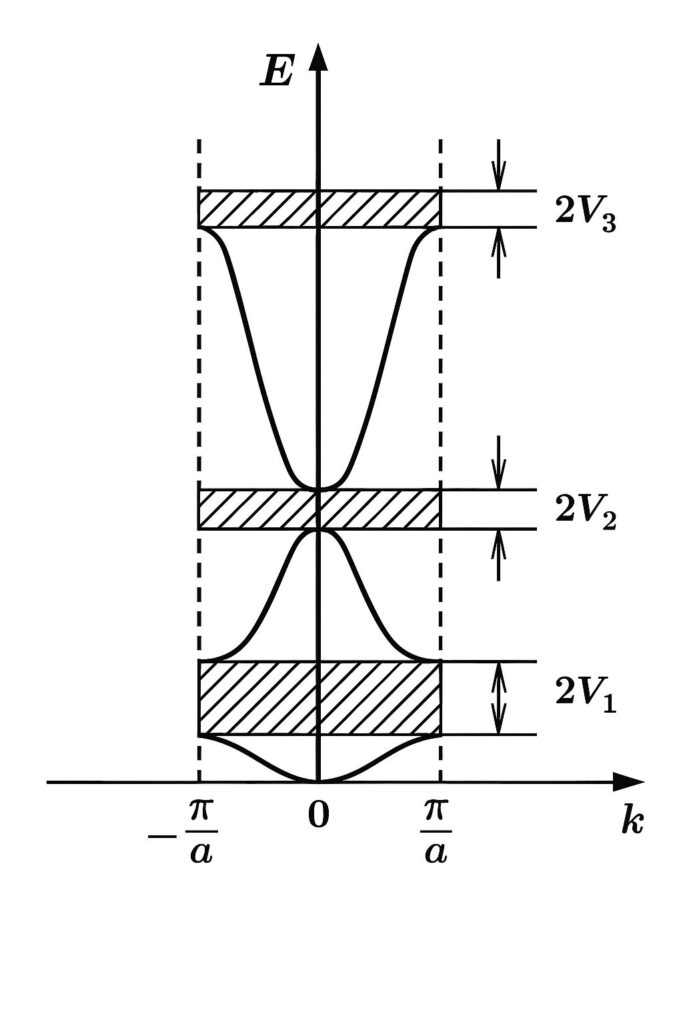
原点を中心とし、格子ベクトル$-\frac{1}{2}\boldsymbol{G}$から$\frac{1}{2}\boldsymbol{G}$の間の領域を第一ブリュアン帯と言います。結晶格子の周期性により、$\frac{1}{2}\boldsymbol{G}$から$\frac{3}{2}\boldsymbol{G}$も第一ブリュアン帯と同じ特性を示します。領域だけ異なるので第二ブリュアン帯と言い、原点から離れていくにつれ、第三、第四と続いていきます。
本問では、第一ブリュアン帯におけるエネルギーギャップを考えましたが、一般的に下記のように表されることが分かっています。