アインシュタインのモデルに基づき、3次元固体の比熱に関して考える。1次元調和振動子の平均エネルギーを(1)式とし、下記の問に答えよ。
\begin{aligned}<E>=\dfrac{h \nu}{e^{\frac{h \nu}{kT}}-1}\end{aligned}
問1:原子量を$M$、モル分子数を$N_{o}$、ボルツマン係数を$k$とする。3次元固体の内部エネルギー$U$を算出し、内部比熱$C$を求めよ。
問2:高温領域$(kT \gg h \nu)$であるとき、$e^{\frac{h \nu}{kT}} \sim 1+\frac{h \nu}{kT}$と近似できる。内部比熱$C_{1}$を求めよ。
問3:低温領域$(kT \ll h \nu)$であるとき、内部比熱$C_{2}$を求めよ。また、理由も述べよ。
問4:絶縁体と導体それぞれについて、電子は比熱にどのように影響しているか説明せよ。
固体の比熱
1gの物質を1K上昇させるのに必要な熱量を言います。比熱が大きいほど同じ熱量で上昇する温度が小さく、小さいほど同じ熱量で上昇する温度は大きいです。高校物理で、何となく覚えている方も多いかもしれませんね。
本記事では、固体の比熱を構成する要素と影響しろを考えていきます。構成する要素については、外部から与えた熱量が固体中でどのように内部エネルギーに変換されるのかを明確にすれば良いです。結論、熱による格子振動のエネルギーと電子のエネルギー変化に基づきます。
本記事では、問題を解くことで両者の依存性を考えていきます。
比熱の導出
熱力学で勉強したように、内部エネルギー$U$の温度微分で表されます。
\begin{aligned}C=\dfrac{\partial U}{\partial T}\end{aligned}
本問では、問1においてこの関係を用います。(1)式は一次元のものですから、三次元に変換することに注意します。
1次元調和振動子の平均エネルギーの導出
様々な方法がありますが、本記事では高校数学(数列)で説明できる下記の方法で説明します。
一次元調和振動子のエネルギーを下記のようにおきます。
\begin{aligned}E=n h \nu\end{aligned}
\begin{aligned}<E>&=\dfrac{調和振動子全体のエネルギーの総和}{調和振動子全体に存在する粒子の個数} \\ &=\dfrac{\sum^{\infty}_{n=0} nh \nu e^{-nh \nu/kT}}{\sum^{\infty}_{n=0} e^{-nh \nu/kT}} \\ &=\dfrac{h \nu(e^{-h \nu/kT}+2e^{-2h \nu/kT} \cdots)}{1+e^{-h \nu/kT}+e^{-2h \nu/kT} \cdots}\end{aligned}
$x=-h \nu/kT$とおくと、
\begin{aligned}<E>&=h \nu \dfrac{(e^{x}+2e^{2x}+\cdots)}{1+e^{x}+e^{2x}+\cdots} \\ &=h \nu \dfrac{d}{dx}\int\dfrac{(1+e^{x}+e^{2x}+\cdots)^{\prime}}{1+e^{x}+e^{2x}+\cdots}dx \\ &=h \nu \dfrac{d}{dx}\log(1+e^{x}+e^{2x}+\cdots) \\ &=h \nu \dfrac{d}{dx}\log\dfrac{1}{1-e^{x}} \\ &=\dfrac{h \nu}{e^{-x}-1} \\ &=\dfrac{h \nu}{e^{h \nu/kT}-1}\end{aligned}
解答例
問1 比熱の導出
三次元固体の内部エネルギーは、(1)式を3倍し
\begin{aligned}U&=3N_{o}<E> \\ &=3N \dfrac{h \nu}{e^\frac{h \nu}{kT}-1}\end{aligned}
これを温度微分することで、求める比熱は
\begin{aligned}C&=3N_{o}h \nu \dfrac{\dfrac{h \nu}{kT^{2}}e^{\frac{h \nu}{kT}}}{(e^{\frac{h \nu}{kT}}-1)^{2}} \\ &=3N_{o} k \dfrac{\left(\dfrac{h \nu}{kT}\right)^{2}e^{\frac{h \nu}{kT}}}{(e^{\frac{h \nu}{kT}}-1)^{2}}\end{aligned}
問2 高温領域における比熱
(7)式に問題文で与えられた近似式を用いることで
\begin{aligned}C_{1}&=3N_{o}k \left(\dfrac{h \nu}{kT}\right)^{2}\dfrac{1+\dfrac{h \nu}{kT}}{\left(\dfrac{h \nu}{kT}\right)^{2}} \\ &=3N_{o}k\left(1+\dfrac{h \nu}{kT}\right)\end{aligned}
$(kT \gg h \nu)$より、$\dfrac{h \nu}{kT} \sim 0$なので
\begin{aligned}C_{1}=3N_{o}k\end{aligned}
であることが分かりました。今までの比熱の式は、指数関数の累乗で表されており、難解なものでした。一方で、高温環境下ではモル分子とボルツマン係数の積で表されることが分かります。これをデュロン・プティの法則と言います。
問3 低温領域における比熱
$(kT \ll h \nu)$より、(7)式の分母$(e^{\frac{h \nu}{kT}}-1) \sim e^{\frac{h \nu}{kT}}$と近似できる。
\begin{aligned}C_{2}&=3N_{o}k \dfrac{\left(\frac{h \nu}{kT}\right)^{2}}{e^{\frac{h \nu}{kT}}}\end{aligned}
$(kT \ll h \nu)$より、$e^{\frac{h \nu}{kT}} \sim \infty$より
\begin{aligned}C_{2}=0\end{aligned}
比熱は0になりました。これは、結晶中における熱励起できる粒子の減少を意味します。$(kT \ll h \nu)$で、$\nu$は振動数を意味するため、調和振動子内の高エネルギーの振動モードは温度によって殆ど励起せず、比熱の減少に寄与します。絶対零度付近になると、これが顕著になるため、比熱は0に漸近します。
結局、比熱は温度に対し下記の依存性になります。
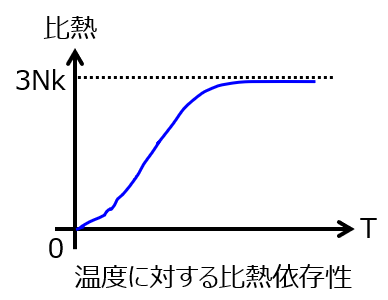
問4 絶縁体と導体における電子比熱
問3までは、格子振動による比熱を考えてきましたが、最後に、電子比熱についても触れます。
絶縁体は、半導体のバンド構造でも触れたように、バンドギャップが大きいです。このため、低温では熱励起が起こらず、電子比熱はほぼ0になります。温度を上げていくことで指数関数的に増加します。
一方で、導体の場合はバンドギャップが小さいです。このため、温度に対し線型的に比熱が増加します。