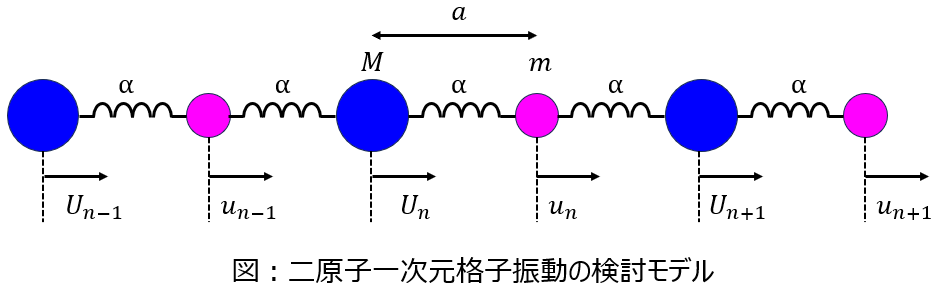
下記のように、質量\(M,m\)の質点A,Bが距離\(a\)ごとにばねを介して交互に並ぶ振動モデルを考える。n番目の質点A,B をx方向に変位させたとき,基準点からの変位をそれぞれ \(U_{n},u_{n}\) とする。ばね定数を\(\alpha\)とし、以下の問に答えよ.
(1)n番目の質点A,Bの運動方程式を求めよ。ただし、隣の質点A,Bの変位\(U_{n-1},u_{n-1},U_{n+1},u_{n+1}\)を用いて良い。
(2)\(U_{n}=A_{M}\exp{j(kna-\omega t)},u_{n}=A_{n}\exp{j(kna-\omega t)}\)とするとき、角周波数\(\omega\)を求めよ。ただし、\(k\)は波数とする。
はじめに
本問は、一見力学に関する問題ですが、物性物理学の分野でよく使用されるモデルになっています。結晶格子の振動の特性を理解する上で頻繁に用いられます。
結晶を構成する原子同士の間で、相互を結びつける結合力が働いているからです。この現象をばねで表現し、熱などによる外乱を受けることを初期位置に対する変位で表現しています。
どこかの方向へ変位を受けた時、ばねの吸引力または反発力により振動が格子全体へ波及することが考えられます。この時の振る舞いを本来は三次元で考えるべきですが、教科書では簡単化のため一次元で説明していることが多いです。無論、試験問題としても計算の大変さから一次元で出題されることが多いです。
よって、本記事でも一次元のモデルで問題の提案と振動の特性を見ていきます。
やっていることは、運動方程式を微分方程式として表し、ある解を仮定して解く数学的作業と変わりません。ただし、計算が少々複雑ですので、本記事で流れを理解しましょう。
解答例
(1)質点A,Bの運動方程式
隣の原子との相対変位\(u_{n}-U_{n},u_{n-1}-U_{n}\)に注目して
\begin{aligned}M\dfrac{d^{2}U_{n}}{dt^{2}}&=\alpha(u_{n}-U_{n})+\alpha(u_{n-1}-U_{n}) \\ &=\alpha(u_{n}+u_{n-1}-2U_{n})\end{aligned}
質点Bについても同様にして
\begin{aligned}m\dfrac{d^{2}u_{n}}{dt^{2}}=\alpha(U_{n+1}+U_{n}-2u_{n})\end{aligned}
(2)角周波数の計算
与えられた式を問(1)の結果に代入し
\begin{cases}-\omega^{2}MA_{M}=\alpha A_{m}(1+\exp(-jka))-2 \alpha A_{M} \\ -\omega^{2}mA_{m}=\alpha A_{M}(1+\exp(-jka))-2 \alpha A_{m}\end{cases}
これを\(A_{M},A_{m}\)についてまとめると
\begin{aligned}\begin{pmatrix}2 \alpha -M\omega^{2} & -\alpha(1+\exp(-jka)) \\ -\alpha(1+\exp(-jka)) & 2 \alpha -m \omega^{2}\end{pmatrix}\begin{pmatrix}A_{M} \\ A_{m}\end{pmatrix}=\begin{pmatrix}0 \\ 0 \end{pmatrix}\end{aligned}
任意の\(A_{M},A_{m}\)に対し右辺が0になるためには、左辺の行列の行列式が0になる必要があり
\begin{aligned}\begin{vmatrix}2 \alpha -M\omega^{2} & -\alpha(1+\exp(-jka)) \\ -\alpha(1+\exp(-jka)) & 2 \alpha -m \omega^{2}\end{vmatrix}=0\end{aligned}
\begin{aligned}Mm\omega^{4}-2 \alpha(M+m)\omega^{2}+2\alpha^{2}(1-\cos ka)=0\end{aligned}
\begin{aligned}\omega_{\pm}^2 = \frac{\alpha(M+m)}{Mm} \left \lbrack 1 \pm \left \lbrace 1 – \frac{4Mm}{(M+m)^2} \sin^2\left(\frac{ka}{2}\right) \right \rbrace^{\frac{1}{2}} \right \rbrack\end{aligned}
何も誘導が無ければ、ここまでを答えとして良いですが、教科書的には下記の説明が続きます。
補足:波数によるモードの変化
前節の結果は、波数\(k\)によって取りうる値が変化します。本問は、「力学」としての出題なので補足扱いとしましたが、「電子物性」としての出題であればここまで問われることがあります。
(i)\(k=0\)のとき
\begin{cases}\omega_{+}^{2} =\dfrac{2 \alpha (M+m)}{Mm} \\ \omega_{-}^{2}=0\end{cases}
(ii)\(k\)が十分に小さく、\(\sin\left(\frac{ka}{2}\right) \sim \frac{ka}{2}\)と近似できるとき
\begin{cases}\omega_{+}^{2} =\dfrac{2 \alpha (M+m)}{Mm} \\ \omega^{2}_{-}-\dfrac{\alpha k^{2}a^{2}}{2(M+m)}\end{cases}
(iii)\(\sin\left(\frac{ka}{2}\right)=1,k=\frac{\pi}{a},M>m\)のとき
\begin{cases}\omega_{+}^{2} =\dfrac{2 \alpha}{m} \\ \omega_{-}^{2} =\dfrac{2 \alpha}{M}\end{cases}
\(\omega_{-}^{2}\)のモードは、単原子1次元格子振動と同じ性質を持ちます。本記事では、二原子を系として与えていますが、振動数としては単原子のモードも存在します。波数\(k\)が0に近づくにつれて\(\omega_{-}^{2}\)も0に近づく性質があります。音波が物質中を伝搬する性質と同じであることから、音響モードと呼ばれています。
一方で、\(\omega_{+}^{2}\)のモードは、二原子を系とした場合に発生する特徴的な振動です。波数が0に近づいても0に近づくことは無く、\(\frac{2 \alpha (M+m)}{Mm}\)に近づきます。隣り合った二種の原子は質量に反比例して互いに反対方向に運動しています。この振動により、電気的な偏極波が生じることから、光学モードと呼ばれています。
参考文献
半導体物性 小長井誠(著) P47~P49