ブレイトンサイクルの理論熱効率、T-S線図の作図例題

問題

下記にブレイトンサイクルの機器構成図を示す。作動流体の比熱比を$\gamma$、圧縮機入口と出口の圧力比を$\beta$、最高温度比を$\tau$として下記の問いに答えよ。

問1：ブレイトンサイクルのT-S線図、P-V線図を作図せよ。
問2：$T_2,T_3,T_4$を$T_1,\gamma,\beta,\tau$を用いて表せ。
問3：ブレイトンサイクルの理論熱効率を$\gamma,\beta$を用いて表せ。

ブレイトンサイクルとは
1. ブレイトンサイクルとオットーサイクルの違い
2. 再生サイクル/再熱サイクル
解答例
最後に

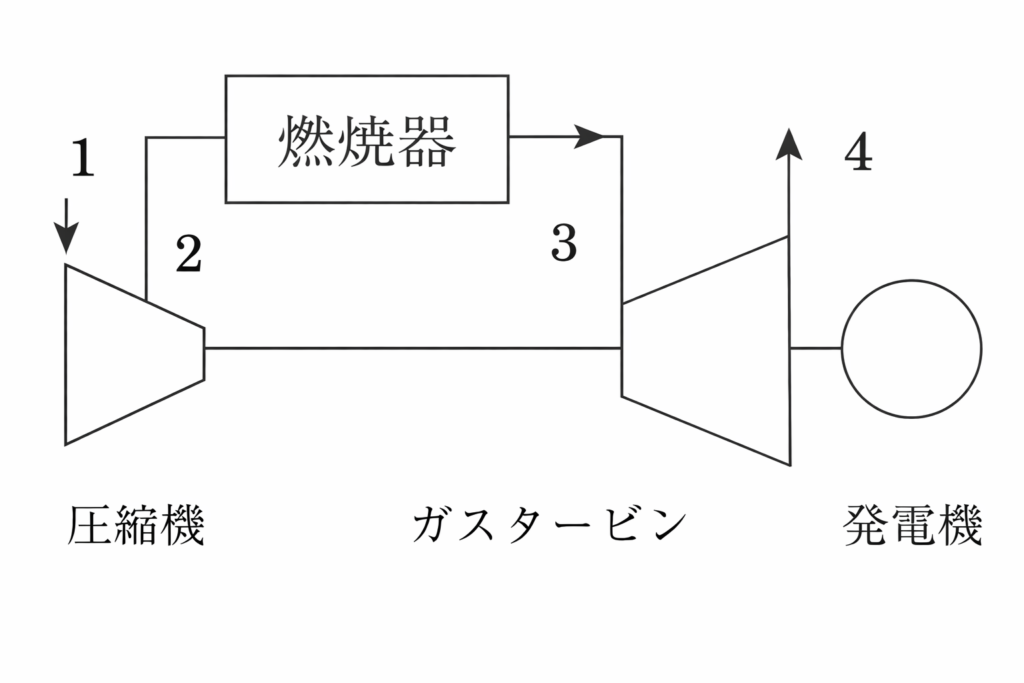
ブレイトンサイクルとは

ガスタービンを初めとする産業用機器で使用する理論熱サイクルです。(ジュールサイクルとも呼ばれます。)
以前の記事では、ガソリンエンジンに使用するオットーサイクルを説明しました。これは、等積加熱によりサイクルを回っていましたが、ブレイトンサイクルは、等圧加熱過程を経る熱サイクルになります。サイクルを経る形態に違いがあります。

問題で与えた過程1→2→3→4はそれぞれ下記の形態変化を取ります。

ブレイトンサイクルの形態変化

過程1→2 断熱圧縮
過程2→3 定圧加熱
過程3→4 断熱膨張
過程4→1 定圧冷却

過程1→2、3→4はオットーサイクルと変わらず断熱過程です。ただし、過程2→3、4→1は、定積だったものが定圧に変わります。

T-S線図を作図する際、等積加熱過程は、等圧加熱過程に対し縦長に変化します。このため、オットーサイクルは縦長のサイクル、ブレイトンサイクルは横長の形を取ります。

ブレイトンサイクルとオットーサイクルの違い

代表的な特性に関する違いは、下記の表でまとめられます。

項目	ブレイトンサイクル	オットーサイクル
加熱過程	等圧	等積
回転数	高い	低～中
出力密度	高い	中
部分負荷効率	著しく低い	低い

加熱過程に大きな違いがあります。
オットーサイクルは等積、ブレイトンサイクルは等圧になる理由として、機械的な構造によることが大きいです。前者は、ガソリンエンジンのピストンが上死点付近でほぼ停止しており、燃焼時間も非常に短く、その時の体積変化を理想的には無視できることから定積とみなしています。
一方で、後者の場合は燃焼器が開放されていることが影響しています。前段のコンプレッサーで流体の圧縮を行い、後段の燃焼器で温度の上昇を行いますが、構造上流体の閉じ込めができません。このため、定積でなく、圧力一定の条件下で加熱していると考えて、本サイクルが生まれています。

回転数は、ブレイトンサイクルの方が高くなります。
ガスタービンは羽の形をしており、流体からの仕事により直接回転運動をするからです。一方で、オットーサイクルの場合は、ピストンの往復運動が大元で必要になります。高回転数にするには、単位時間あたりのピストンの往復運動数を増やす必要がありますが、振動など、機械的な制約上厳しいです。
回転数が高いことから、出力密度もブレイトンサイクルの方が高くなります。

部分負荷効率はどちらも低くなります。
オットーサイクルの方が比較的マシなくらいです。オットーサイクルの場合、エンジンの吸気を絞ることで実現できます。吸気圧が下がるものの、損失も下がるため、ある程度の効率低下になります。一方で、ブレイトンサイクルの場合は、供給燃料の流量を減らすことで部分負荷運転を実現できます。ただし、コンプレッサによる圧縮仕事(入力)はほぼ変わらないのに対し、タービン入り口の温度が下がるため、仕事量(出力)が減ってしまいます。この関係により、部分負荷効率は著しく低くなります。

再生サイクル/再熱サイクル

ブレイトンサイクルの熱効率は、30~40%程度です。半分以上は損失となっています。そこで、熱効率を少しでも高めようと考案されたのが再生サイクルです。下記の概要図を示します。ガスタービンから出て来た排気を用いて、圧縮機から出て来た空気を加熱する構成になっています。排気熱の有効利用により、熱効率が向上する効果があります。

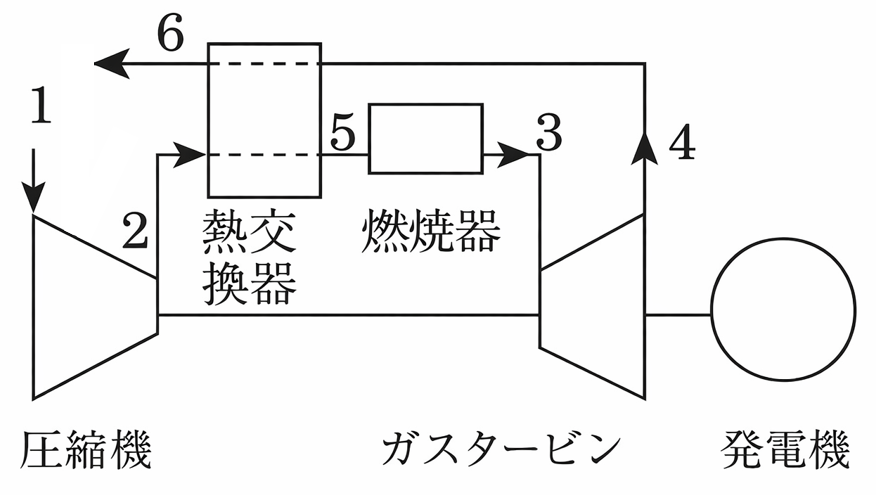
他、再熱サイクルにより、出力を向上させる機器構成もあります。タービンを複数用意し、一つ目の高圧タービンの出口から出てきた気体を再加熱し、低圧(または中圧)タービンに投入することで仕事量を増やし、熱効率の向上を図ることができます。注意点として、低圧タービン中の気体は圧力が低いため、湿り蒸気となりやすいです。水滴により、高速で回るタービンの羽根が傷つくエロージョンが発生しないように設備設計をする必要があります。

再生サイクルも、再熱サイクルも電験では頻出になっています。是非覚えましょう。

解答例

問1 P-V線図、T-S線図の作図

これは、オットーサイクルの記事で紹介した方法と同じ要領で作図すれば良いです。断熱過程のエントロピーは変化しないこと=T-S線図のy軸：Tだけ移動することに注目して作図することが基本です。一方で、定圧過程については、P-V線図を作図するときにVだけ変化させることに生きてきます。

冒頭で、過程1→2、3→4は断熱。過程2→3、4→1は定圧であることを説明しました。よって下記の概形になります。

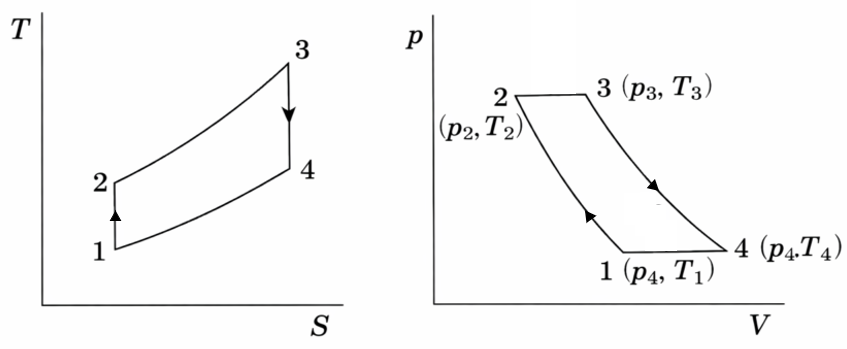
問2 $T_2,T_3,T_4$の温度

断熱過程、定圧過程

まず、過程1→2について断熱圧縮より，
\begin{aligned}
\frac{T_2}{T_1} = \beta^{\frac{\gamma-1}{\gamma}}
\end{aligned}

したがって，
\begin{aligned}
T_2 = T_1 \, \beta^{\frac{\gamma-1}{\gamma}}
\end{aligned}

次に、過程2→3に注目し、$T_3$を求める。
最高温度比の定義より，
\begin{aligned}
\tau = \frac{T_3}{T_1}
\end{aligned}
よって，
\begin{aligned}
T_3 = \tau T_1
\end{aligned}

最後に、過程3→4に注目し、$T_4$を求める。

\begin{aligned}
\frac{T_4}{T_3} = \beta^{-\frac{\gamma-1}{\gamma}}
\end{aligned}

したがって，
\begin{aligned}
T_4 = T_3 \, \beta^{-\frac{\gamma-1}{\gamma}}
= \tau T_1 \beta^{-\frac{\gamma-1}{\gamma}}
\end{aligned}

問3 熱効率

理論熱効率は，入力熱量$Q_{in}$とタービンの仕事$Q_{in}-Q_{out}$の比を用いて
\begin{aligned}
\eta =1 – \frac{Q_{\text{out}}}{Q_{\text{in}}}
\end{aligned}
で定義される。

定圧過程における熱量より，定圧比熱を$c_p$とすると
\begin{cases}
Q_{\text{in}} = c_p (T_3 – T_2) \\
Q_{\text{out}} = c_p (T_4 – T_1)
\end{cases}

したがって，
\begin{aligned}
\eta &= 1 – \frac{Q_{\text{out}}}{Q_{\text{in}}}
\\ &= 1 – \frac{T_4 – T_1}{T_3 – T_2}
\end{aligned}

ここで (2) の結果を代入すると，
\begin{aligned}
\eta
= 1 – \frac{\tau T_1 \beta^{-\frac{\gamma-1}{\gamma}} – T_1}
{\tau T_1 – T_1 \beta^{\frac{\gamma-1}{\gamma}}}
\end{aligned}

整理すると，ブレイトンサイクルの理論熱効率は，