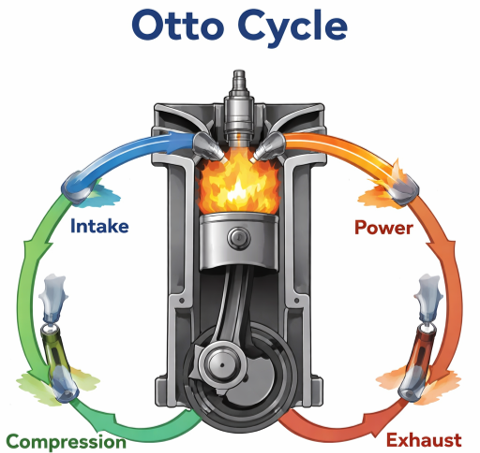
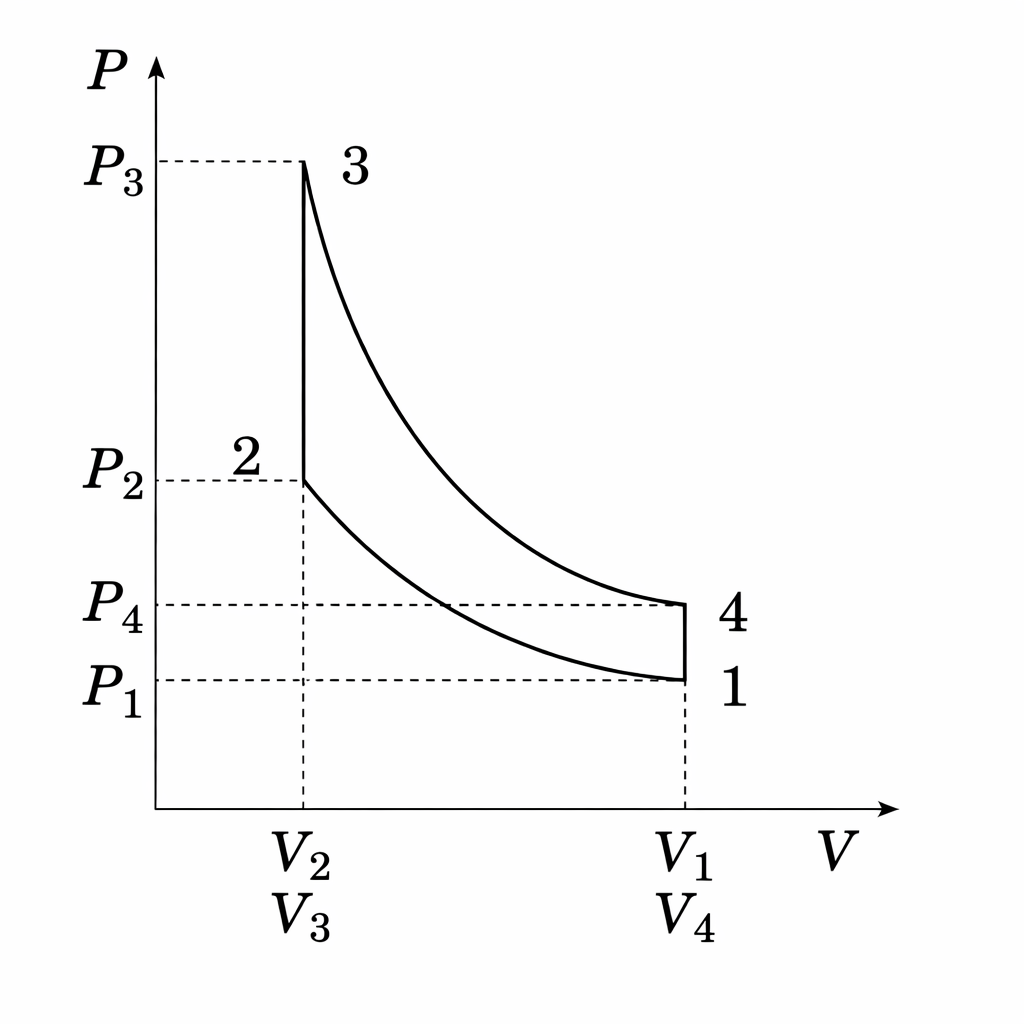
下記にオットーサイクル(P-V線図)を示す。圧縮比を$\varepsilon=\frac{V_1}{V_2}$、圧力比を$\xi=\frac{P_3}{P_2}$、比熱比を$\gamma$、質量を$M$、定積比熱を$C_v$とし理想気体の条件下において、下記の問に答えよ。
問1:$T_1,T_2,T_3$を$T_4,\varepsilon,\xi,\gamma$で表せ。
問2:理論熱効率$\eta$を$\varepsilon,\xi,\gamma$で表せ。
問3:このサイクルのT-S線図(縦軸:T、横軸:S)を示せ。
問4:点2におけるエントロピー$S_2$を$S_3,M,C_v,T_2,T_3$を用いて表せ。
オットーサイクルとは
ガソリンエンジンの理想的な熱サイクルを表したものになります。ガソリンエンジンは、圧縮→燃焼→膨張→排気の過程を経ますが、オットーサイクル上では下記の動作が対応します。
- 断熱圧縮:圧縮に対応 (過程1→2)
- 定積加熱:燃焼に対応 (過程2→3)
- 断熱膨張:膨張に対応 (過程3→4)
- 定積冷却:排気に対応 (過程4→1)
断熱圧縮(膨張)とは
系に対して熱の出入りが無く内部のピストンを押し下げる/押し上げる(仕事をされる/する)動きになります。熱力学第一法則$Q=\Delta U + W$に対し、$Q=0$のため、下記の式になります。
\begin{aligned}\Delta U=-W\end{aligned}
外部へ仕事をした分だけ、温度が低下する。その逆もあることを示しています。エントロピーに変化は無いため、等エントロピー過程とも言われます。問3にてT-S線図を作図する際は、Sを変化させず縦軸Tのみを変化させます。
この過程において、圧力と体積に対し下記の関係が成立します。(問1を解くために使用します。)
\begin{aligned}PV^{\gamma}=一定\end{aligned}
ここで、$\gamma$は比熱比であり、定圧比熱$C_p$、定積比熱$C_v$の比$C_p/C_v$で表されます。
実世界において、外部からの熱のやり取りは必ず0値になるわけでは無いですが、オットーサイクル上は理想化して考えています。
定積加熱(冷却)とは
体積一定の元、系の内部エネルギーが増加/減少する過程を言います。ピストンは動かない(仕事をしない)ため、熱力学第一法則において、$W=0$となり、下記の式になります。
\begin{aligned}Q=\Delta U\end{aligned}
外部から得たエネルギーがそのまま内部エネルギーの上昇に寄与する。という解釈が出来ます。
なお、変化前の温度を$T_b$、変化後の温度を$T_a$、定積比熱を$C_v$とすると、内部エネルギー変化$\Delta U$は下記の式で表されます。
\begin{aligned}\Delta U=MC_v(T_a – T_b)\end{aligned}
現実には、排気にはエンジンに付属するバルブが開き、外部との熱のやり取りが発生します。オットーサイクルではこの影響は無視し、理想化しています。
熱力学におけるエントロピーとは
エネルギーの散らばり具合を表します。情報理論にもエントロピーは存在しますが、同じ乱雑さを示す点では似たような概念ですね。情報理論では、確率に対し$\log$を取るだけで良かったですが、熱力学に関してはいくつかの約束事があります。
考える状態変化の過程により、下記の2通りに分類される。
- 可逆過程の場合:$dS=\frac{dQ}{T}$
- 不可逆過程の場合:$dS>\frac{dQ}{T}$
熱力学の試験では、可逆過程を想定する場合が多く、積分形$S=\int^{A}_{O}\dfrac{dQ}{T}$を用いて問題を解くことが多い。
上記の考え方は、問4に対しふんだんに使います。オットーサイクルだけでなく、熱力学の試験において頻出計算となっています。必ず覚えましょう。
解答例
問1 温度変数
まず、過程3→4を考え、$T_3$を求める。断熱変化だから
\begin{aligned}T_3 V_3^{\gamma -1}=T_4 V_4^{\gamma -1}\end{aligned}
\begin{aligned}T_3=\left(\dfrac{V_4}{V_3}\right)^{\gamma-1}T_4\end{aligned}
過程2→3、4→1は定積変化だから、$V_4=V_1 ,V_3=V_2$。問いで与えた$\gamma$が使えるので
\begin{aligned}T_3=\varepsilon^{\gamma -1}T_4\end{aligned}
次に$T_2$について、状態方程式$PV=nRT$により
\begin{aligned}\dfrac{nRT_2}{P_2}=\dfrac{nRT_3}{P_3}\end{aligned}
\begin{aligned}T_2=\dfrac{P_2}{P_3}T_3=\xi^{-1}\varepsilon^{\gamma-1}T_4\end{aligned}
最後に、$T_1$について、断熱変化であることに注目し
\begin{aligned}T_1V_1^{\gamma -1}=T_2 V_2^{\gamma -1}\end{aligned}
\begin{aligned}T_1=\dfrac{V_2}{V_1}T_2=\xi^{-1}T_4\end{aligned}
問2 理論熱効率
過程2→3で系が吸収する熱量を$Q_{23}$、過程4→1で系が放出する熱量を$Q_{41}$とすると
\begin{cases}Q_{23}=MC_v (T_3-T_2) \\ Q_{41}=MC_v (T_4-T_1)\end{cases}
以上より、理論熱効率は
\begin{aligned}\eta &=1-\dfrac{Q_{41}}{Q_{23}} \\ &=1-\dfrac{T_4- T_1 }{T_3 – T_2} \\ &=1-\dfrac{T_4 – \xi^{-1} T_4}{\varepsilon^{\gamma -1}T_4 – xi^{-1} \varepsilon^{\gamma -1}T_4} \\ &=1-\dfrac{1}{\varepsilon^{\gamma -1} }\end{aligned}
問3 T-S線図
過程1→2、3→4は断熱過程(等エントロピー過程)であることから、下記のようになる。
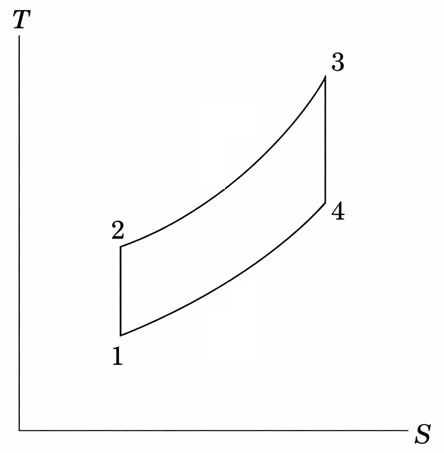
問4 エントロピーの計算
熱力学第一法則 $dU=-PdV+TdS$に対し、状態方程式と$dU=Cv dT$ を用いると
\begin{aligned}dS &= \dfrac{dU}{T} + \dfrac{P dV}{T} \\ &=\dfrac{MC_v dT}{T}+\dfrac{M R dV}{V}\end{aligned}
過程2→3は定積変化だから、$dV=0$。$dS=\dfrac{M C_v}{T} dT$。この過程を積分すると
\begin{aligned}\int^{3}_{2}dS &=S_{3}-S_{2} \\ &=MC_v \int^{3}_{2}\dfrac{dT}{T} \\ &=MC_v \log\dfrac{T_3}{T_2}\end{aligned}
以上より、$S_{3}=S_{2}+MC_v \log\dfrac{T_3}{T_2}$