下記のように、内部に熱源を持たない半無限長の平板の表面に熱振動を与えた時の内部熱伝導を考える。単位体積当たりの熱容量を$C$、熱伝導率を$\lambda$、熱拡散率を$k$とした時、下記の問いに答えよ。
問1:平板表面の温度変化を$T(x,t)=f(x) e^{i \omega t}$とし、$x→\infty$にて$T→T_o$に収束するとしたとき、$f(x)$を求めよ。
問2:表面で与えた角振動数$\omega$の変化は、どの程度の距離$\delta$までしみこむか。表皮深さを求めよ。
問3:問2と同じく表面で角振動数$\omega$の温度変化を与え、$x=h$の点で温度を測定する場合を考える。振幅の大きさや振動の時間遅れから、熱拡散率$k$を見積もる式を示せ。
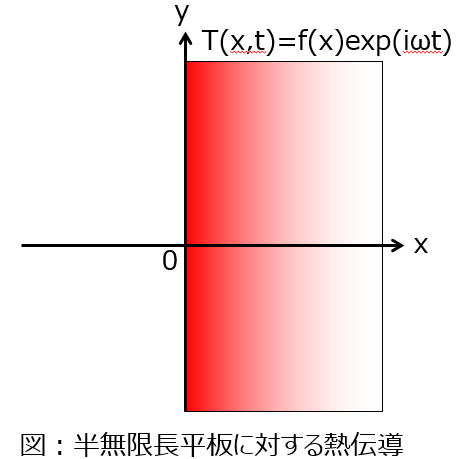
はじめに
本記事では、一次元熱伝導方程式に具体的な条件を与え、手計算で解く記事になります。級数で解く記事は過去に紹介しましたが、本問ではフーリエ変換を用いて解きます。熱伝導方程式に仮定した解を代入し、出て来た数式の評価をして一般解を求めていく作業に変わりないですが、こちらの方が院試で問われやすい内容になります。是非練習しましょう。
一次元熱伝導方程式
ある地点の温度を$T(x,t)$とし、熱拡散率$k$を用いて、下記で表されます。
\begin{aligned}\Delta T(x,t)=k\dfrac{\partial T}{\partial t}\end{aligned}
なお、$k=\dfrac{\lambda}{C}$です。上式の導出については、多数の文献で紹介されていますので割愛します。ある微小体積において流入する熱エネルギーと流出する熱エネルギーの差から、微小時間における温度上昇を算出しています。
本問を解くにあたっての留意点
熱伝導方程式さえ知っていれば、微分方程式を数学的に解く作業と変わりありません。ただし、ネイピア数型の解となり、$e^{-1}$となる表皮深さ$\delta$を求めることが本記事のメイントピックとなります。
電磁気学の表皮効果と類似の事象が、伝熱工学においても当てはまります。過去の記事も参考にしながら、本学問における表皮深さの導出方法を学んでいきましょう。
解答例
問1:f(x)の分布
$T(x) = f(x)e^{i \omega t}$ を熱伝導方程式 (5) に代入すると、
\begin{aligned}
i \omega f(x)e^{i \omega t} = k f^{\prime \prime}(x) e^{i \omega t}
\end{aligned}
\begin{aligned} f^{\prime \prime}(x) = \frac{i \omega}{k} f(x)\end{aligned}
\(\sqrt{i} = \frac{1}{\sqrt{2}} + i \frac{1}{\sqrt{2}} \)により、定数$A,B$を用いると
\begin{aligned}
f(x)= A \exp \left( -\frac{1 + i}{\sqrt{2}} \sqrt{\frac{\omega}{k}} x \right)+B \exp \left( \frac{1 + i}{\sqrt{2}} \sqrt{\frac{\omega}{k}} x \right)
\end{aligned}
$x \to \infty$ で発散しないためには $B = 0$ とすべきだから、
\begin{aligned}
f(x) = A \exp \left( -\frac{1 + i}{\sqrt{2}} \sqrt{\frac{\omega}{k}} x \right)
\end{aligned}
ゆえに、$x = 0$ で $T_0$ のまわりに振幅 $A$ で振動するような解 $T(x, t)$ は、
\begin{aligned}
T(x, t) &= \Re \left[ A e^{-\frac{1+i}{\sqrt{2}} \sqrt{\frac{\omega}{k}} x} e^{i \omega t} + T_0 \right] \\
&= \Re \left[ A e^{-\sqrt{\frac{\omega}{2k}} x} e^{i \left( \omega t – \sqrt{\frac{\omega}{2k}} x \right)} + T_0 \right] \\
&= A e^{-\sqrt{\frac{\omega}{2k}} x}
\cos \left( \omega t – \sqrt{\frac{\omega}{2k}} x \right)\end{aligned}
問2:表皮深さ
(3) \( T(x,t) \) の振幅 \( A e^{-\sqrt{\frac{\omega}{2k}} x} \) が ( 1/e ) になる距離を \( \delta \) とすると、
\begin{aligned}
e^{-\sqrt{\frac{\omega}{2k}} \delta} = e^{-1}, \quad
\therefore \;
\delta = \sqrt{\frac{2k}{\omega}}
\end{aligned}
問3:熱拡散率の見積もり
問題の前提条件により、$T(h,t)$を下記のように設定する。
\begin{aligned}
T(h, t) = A e^{-\sqrt{\frac{\omega}{2k}} h}
\cos \left( \omega t – \sqrt{\frac{\omega}{2k}} h \right) + T_0
\end{aligned}
だから、\( x = h \) での振幅の大きさを \( A_h \) とすると、
\begin{aligned}
A_h = A e^{-\sqrt{\frac{\omega}{2k}} h}, \quad
\therefore \;
k = \frac{\omega h^2}{2 \left( \ln \frac{A}{A_h} \right)^2}
\end{aligned}
または、( x = h ) での振動の時間遅れを \( \Delta t \) とすると、
\begin{aligned}
\omega t – \sqrt{\frac{\omega}{2k}} h
= \omega \left( t – \frac{h}{\sqrt{2k \omega}} \right)
\end{aligned}
より、
\begin{aligned}
\Delta t = \frac{h}{\sqrt{2 k \omega}}
\quad \therefore \quad
k = \frac{h^2}{2 \omega (\Delta t)^2}
\end{aligned}
上記が、熱拡散率$k$を見積もる式である。
最後に
どの科目にも言えますが、微分方程式が与えられたときは、一般解を$e^{ax}$と仮定して解いてみましょう。講義で出てくる問題については、この方法で殆ど解くことができます。