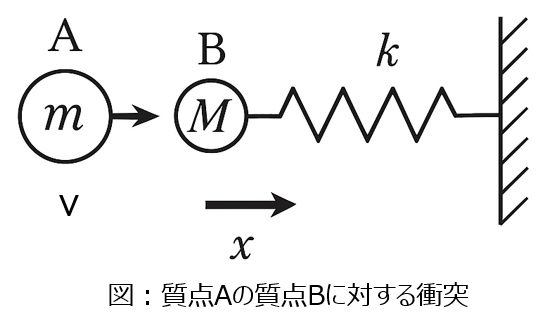
下図のように、速度$v$で運動している質量mの質点Aがばね定数$k$で固定壁に接続されている質量$M$の質点Bに衝突する場合を考える。速度$v$で運動する方向を$x$軸の正の向きとし、下記の問いに答えよ。
問1:衝突時に質点A,Bの二物体が一体となって運動する場合、質点Bの時間変化を求めよ。
問2:弾性衝突であるとき、質点A,Bそれぞれの衝突直後の速度を求めよ。
問3:Mとmの比$r=\frac{M}{m}$を用いて、衝突後の質点A,Bそれぞれの位置の時間変化$x_{A}(t),x_{B}(t)$を求めよ。また、もう一度衝突しないためにはどのような条件を満たせば良いか、定性的に述べよ。
質点の衝突
高校物理でもありましたが、院試でもたまに出題されます。運動方程式を数学的に解く要素が強くなりますが、基本的な法則に基づいて立式する方法に変わりないです。
一般的に、2つの関係式を立てます。
衝突前の質点m,Mの速度をそれぞれ$u_{1},u_{2}$、衝突後の速度をそれぞれ$v_{1},v_{2}$とすると、下記の関係になる。
1.運動量保存則:系全体の運動量は保存する。
\begin{aligned}mu_{1}+Mu_{2}=mv_{1}+Mv_{2}\end{aligned}
2.反発係数を$e$とすると、下記の関係が成立する。
\begin{aligned}e=\dfrac{v_{2}-v_{1}}{u_{1}-u_{2}}\end{aligned}
本問では、質点Bは最初停止しているため、$u_{2}=0$です。これを前提に運動方程式を立てて解いていきます。
なお、問1では衝突後に一体となって運動するため、$e=0$です。逆に、問2では弾性衝突のため、$e=1$です。
解答例
問1 二物体の運動
衝突後の速度を$V$とする。運動量保存則により
\begin{aligned}mv=(m+M)V\end{aligned}
\begin{aligned}V=\dfrac{mv}{m+M}\end{aligned}
次に、衝突後の運動方程式は、mとMが一体になっていることに注意し
\begin{aligned}(m+M)\ddot{x}=-kx\end{aligned}
$x=Ce^{iat}$とすると、$a= \sqrt{\frac{k}{m+M}}$より、一般解
\begin{aligned}x(t)=Ae^{iat}+Be^{-iat}\end{aligned}
初期条件$x(0)=0,\dot{x(0)}=\dfrac{mv}{m+M}$なので
\begin{cases}A+B=0 \\ i a(A-B)=\dfrac{mv}{m+M}\end{cases}
\begin{cases}A=\dfrac{1}{i2a}\dfrac{mv}{m+M} \\ A=-B\end{cases}
\begin{aligned}x(t)&=\dfrac{mv}{a(m+M)}\dfrac{e^{iat}-e^{-iat}}{2i} \\ &=\dfrac{mv}{\sqrt{k(m+M)}}\sin \sqrt{\dfrac{k}{m+M}}t\end{aligned}
問2 衝突後の速度
運動量保存則、反発係数の関係により
\begin{cases}mv=mv_{a}+Mv_{B} \\ -1=\dfrac{v_{a}-v_{B}}{v}\end{cases}
\begin{cases}v_{A}=\dfrac{(m-M)v}{m+M} \\ v_{B}=\dfrac{2mv}{m+M}\end{cases}
問3 再衝突しない条件
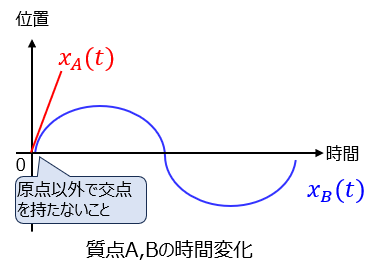
一度目の衝突後の質点A,Bの位置の時間変化を求め、グラフにプロット。交点が発生しないよう評価すれば良いです。
質点Aの時間変化
まず、問2の結果を変形し、$v_{A}$を$r$を用いた式で表す。
\begin{aligned}v_{A}&=\dfrac{1-\frac{M}{m}}{1+\frac{M}{m}} \\ &=\dfrac{1-r}{1+r}V\end{aligned}
衝突後の質点Aの運動方程式を考える。何も外力を受けないため
\begin{cases}\ddot{x_{A}}=0 \\ \dot{x_{A}}=C_{1} \\ x_{A}=C_{1}t+C_{2}\end{cases}
$\dot{x_{A}}(0)=v_{A}=\frac{1-r}{1+r}V,x_{A}(0)=0$であるため
\begin{cases}C_{1}=\dfrac{1-r}{1+r}Vt \\ C_{2}=0\end{cases}
\begin{aligned}x_{A}(t)=\dfrac{1-r}{1+r}Vt\end{aligned}
と、衝突後の質点Aの位置の時間変化が分かりました。
質点Bの時間変化
質点Aと同様の手順で解いていく。問2の$v_{B}$を$r$を用いて表す。
\begin{aligned}v_{B}&=\dfrac{2mV}{m+M} \\ &=\dfrac{2}{1+r}V\end{aligned}
質点Bの運動方程式は、ばねの拘束力が働いているので
\begin{aligned}\ddot{x_{B}}=-\dfrac{k}{M}x\end{aligned}
$\omega_{B}=\frac{k}{M}$とすると、一般解は
\begin{aligned}x_{B}(t)=Ae^{i \omega_{B}t}+Be^{-i \omega_{B}t}\end{aligned}
$\dot{x_{B}}(0)=v_{B}=\frac{2}{1+r}V,x_{B}(0)=0$であるため
\begin{cases}A+B=0 \\ i \omega_{B}(A-B)=\frac{2}{1+r}\end{cases}
\begin{aligned}2i \omega_{B}A=\dfrac{2}{1+r}V\end{aligned}
\begin{cases}A=\dfrac{V}{i \omega_B(1+r)} \\ B=-\dfrac{V}{i \omega_B(1+r)}\end{cases}
\begin{aligned}x_{B}(t)&=\dfrac{V}{\omega_B(1+r)}\left(\dfrac{e^{i \omega_{B}t}}{i}-\dfrac{e^{-i \omega_{B}t}}{i}\right) \\ &=\dfrac{2V}{1+r}\sqrt{\dfrac{M}{k}}\sin \sqrt{\dfrac{k}{M}}t\end{aligned}
(15)式、(21)式の交点が存在しない条件を満たすとき、質点A,Bは再衝突しない。