ジュールトムソン係数$\mu_{JT}$を下記の式で与える。
\begin{aligned}\mu_{JT}&=\left(\dfrac{\partial T}{\partial p}\right)_{H} \\ &=\dfrac{1}{C_p}\left \lbrace T\left(\dfrac{\partial V}{\partial T}\right)_{p}-V \right \rbrace \end{aligned}
問1:理想気体における$\mu_{JT}$を求めよ。
問2:実在気体をファンデルワールス状態方程式として、下記の式で与える。この時の$\mu_{JT}$を求めよ。ただし、$a,b$は小さく、一次近似を用いて良い。
\begin{aligned}\left ( p+ \dfrac{a}{V^{2}}\right) (V-b)=RT\end{aligned}
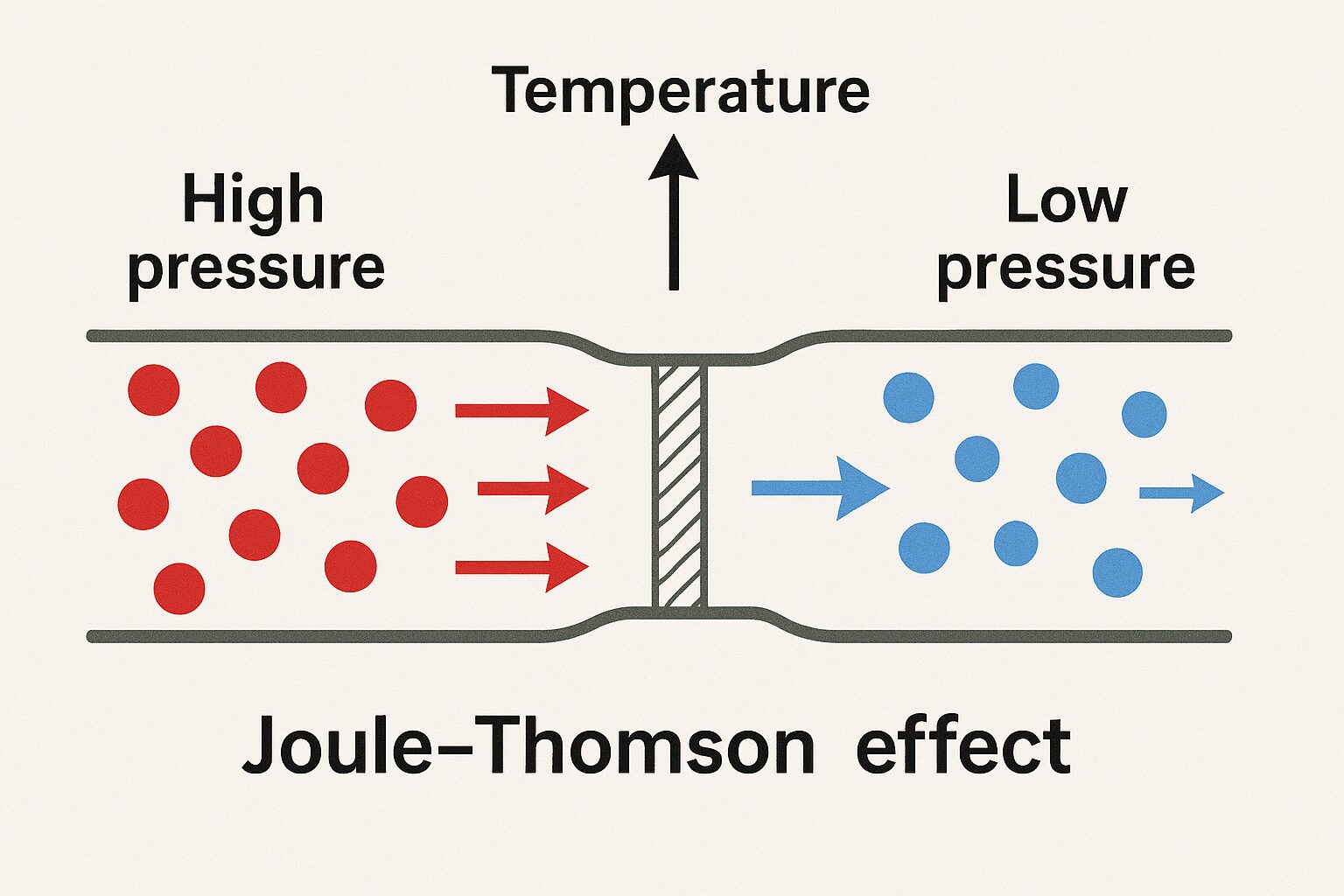
ジュールトムソン効果とは
実在気体が等エンタルピー変化をすると、分子間力によって温度が変化する現象を言います。工学分野においては、工場における減圧弁などで本現象は観測されます。$\mu_{JT}$の正負によって、下記の関係になります。
- $\mu_{JT}>0$のとき、気体が膨張する(圧力が下がる)と温度が下がる。(冷却)
- $\mu_{JT}<0$のとき、気体が膨張する(圧力が下がる)と温度が上がる。(加熱)
※$|\mu_{JT}|$が大きいほど、上記の傾向は顕著となる。
理想気体は分子間力を持ちませんが、実在気体はこれを持ちます。
分子間力は、引力成分と斥力成分の二つが存在します。(2)式はその関係を表しており、$a$は引力成分、$b$は斥力成分を示します。引力成分が強いほど冷却に寄与し、斥力成分が強いほど加熱に寄与します。その理由を問2で考えましょう。
なお、院試では、ジュールトムソン係数(式(1))の導出を求められる場合があります。エンタルピーを全微分することを起点に証明するように求められる場合が多いですが、専門書にも記載されていることが多いため、ここでは省略します。
また、ファンデルワールスの状態方程式を用いて実在気体の物性を考える問題も出題される場合もあります。本記事に限らず広く使う内容ですので、教養として持っておきましょう。
解答例
問1 理想気体におけるジュールトムソン係数
$PV=nRT$を変形すると、$V=\frac{nRT}{P}$。これを(1)式の{}内に代入することにより
\begin{aligned}\mu_{JT} & \sim T\left(\dfrac{\partial V}{\partial T}\right)_{p}-V \\ &=T ・ \dfrac{nR}{p}-V \\ &= V- V \\ &=0\end{aligned}
以上より、ジュールトムソン効果は起こらない。
※理想気体には分子間力が存在しないため、当たり前の現象かもしれませんが、実際に数式で証明することができました。
問2 実在気体におけるジュールトムソン係数
まず、(2)式を展開すると
\begin{aligned}pV-pb+\dfrac{a}{V}-\dfrac{ab}{V^{2}}=RT\end{aligned}
2次項$V^{2}$を無視し、$a,b$は小さいため、$pV \sim RT$を用いて良く
\begin{aligned}pV=RT+pb-\dfrac{a}{V} \\ V=\dfrac{RT}{p}+b-\dfrac{a}{RT}\end{aligned}
$\dfrac{\partial V}{\partial T}=\dfrac{R}{p}+\dfrac{a}{RT^{2}}$により、(2)式の{}に代入すると
\begin{aligned}T\left(\dfrac{\partial V}{\partial T}\right)_{p}-V &=\left(\dfrac{RT}{p}+\dfrac{a}{RT}\right)-\left(\dfrac{RT}{p}+b-\dfrac{a}{RT}\right) \\ &=\dfrac{2a}{RT}-b\end{aligned}
以上より、求めるジュールトムソン係数は
\begin{aligned}\mu_{JT}=\dfrac{1}{C_p}\left ( \dfrac{2a}{RT}-b \right)\end{aligned}
$a$(引力)が大きいとき、$\mu_{JT}>0$となり、冷却側に働く
$b$(斥力)が大きいとき、$\mu_{JT}<0$となり、加熱側に働く
多くの気体は常温環境下で冷却側に働きますが、水素とヘリウムに関しては引力が小さく、加熱側に働くことは参考として覚えておきましょう。
最後に
本分野は、社会に出て配管設計をする際に出てきます。決して、机上で済む話ではありません。電気系の学生はこれを習わずに就職して、配属先で怒られる場合もあります。(筆者がそうでした。)
そんなことが無いように、覚えておくと身を助けます。