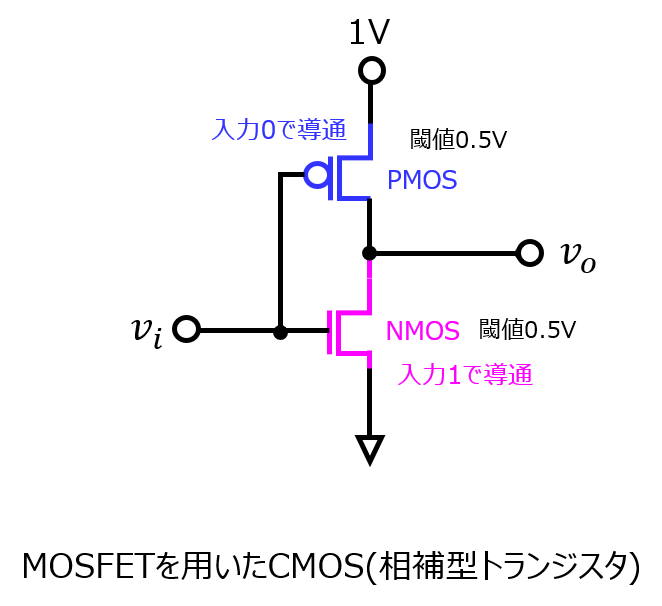
図1にPMOS、NMOSを組み合わせたCMOS(相補型トランジスタ)を示す。
(1)入力電圧\(v_{in}\)と出力電圧\(v_{o}\)特性を用いて動作原理を述べよ。なお、PMOSとNMOSの閾値電圧を0.5Vとする。
(2)相補型トランジスタの利点を述べよ。また、動作を考えるうえで留意すべき点を述べよ。
(3)CMOSの動的消費電力を求めよ。ただし、容量を\(C\)、電源電圧を\(V_{c}\)、動作周波数を\(f\)、スイッチング確率を\(\eta\)、PMOSとNMOSの導通関係が切り替わる時間を\(T\)とする。
CMOS(相補型トランジスタ)とは
図1のように、PMOSとNMOSを直列に並べたトランジスタです。
以前の記事で紹介したように、入力電圧が所定値以下のときは、PMOSが導通するので出力は上位の電圧になります。
逆に所定値以上のときはPMOSは導通しなくなるので、出力電圧は0Vになります。
主に、論理回路として使用していきますが、内部ではどのような物理現象が発生しているのか。電子回路として見ていきましょう。
解答例
(1)入力電圧-出力電圧特性
論理回路を思い出しましょう。
前章の説明の通りの動作をしますので、下記の特性で表すことができます。

閾値電圧を境に、出力電圧が急峻に立ち下がります。
(2)CMOSの利点と欠点
利点1
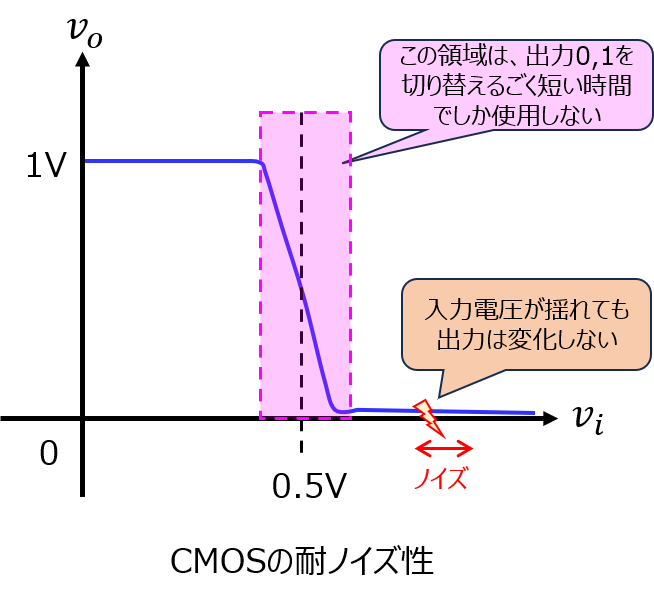
耐ノイズ性が高いことです。
(1)の電圧特性がヒントです。
閾値電圧付近以外では、出力が一定です。
論理回路として使用するとき、入力電圧は0Vか1Vのmin maxの2択です。
よって、少しのノイズが発生しても、出力電圧は全く変化しないことが分かります。
利点2
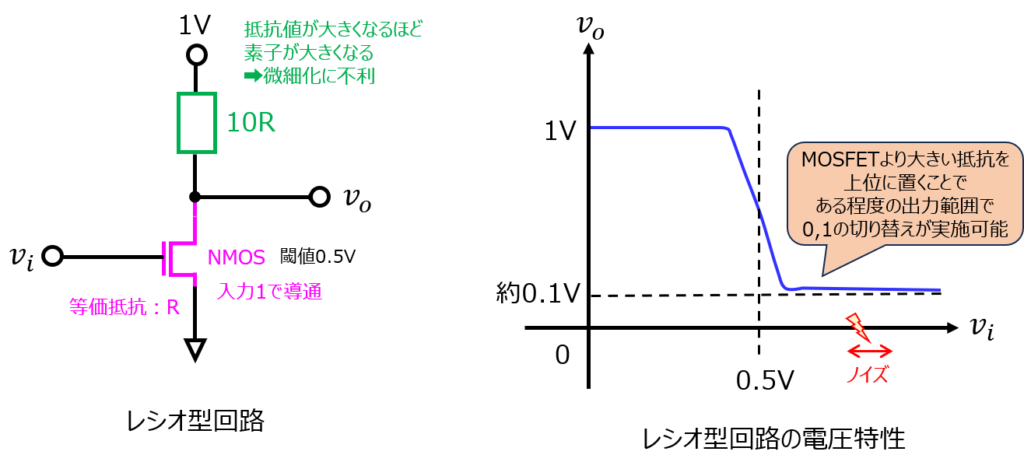
使用面積が小さいことです。(微細化しやすい)
CMOSに対して、下記のようなレシオ回路でも論理回路を構成することができます。
動作原理としては、CMOSと同じです。入力電圧を上げていくと、NMOSが導通するようになり、出力電圧が下がることで0,1を判断します。
しかし、このためには、NMOSの抵抗値に対し非常に大きい抵抗を準備する必要があります。
NMOSが導通したとき、出力電圧を0.1倍にしたいときは、抵抗値をNMOSの約10倍に設定する必要があり、物理的に大きくなります。
そうなると、回路の集積化に不利になります。
この抵抗をPMOSにすることで、導通していないときは抵抗値無限大になります。また、抵抗よりも物理的に小さいため、集積化に有利となります。
留意点
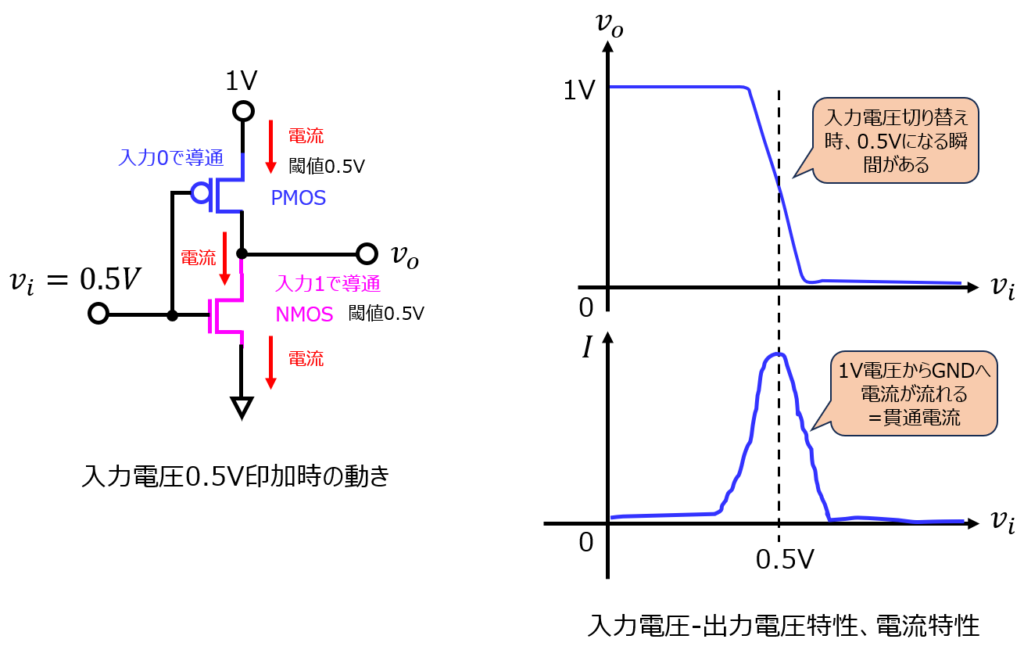
PMOSとNMOSのスイッチが切り替わるとき、貫通電流が発生することです。
貫通電流とは、直流電源電圧がそのままGNDへ流れることを指します。
先の説明通り、入力電圧が閾値電圧に到達したとき、PMOSとNMOSの導通の関係が変わります。
しかし、理想的に入れ替わるわけではなく、厳密には両方導通している時間も存在します。
また、製造誤差(物バラ)により、PMOSの閾値電圧は0.51V、NMOSの閾値電圧は0.49Vの時もあります。
この時、入力電圧がそのままGNDに流れます。(貫通電流)
電流が無駄にGNDに流れており消費電力が大きくなってしまいます。
対策としては、入力電圧を速やかに閾値電圧を超えるように、スイープ速度を上げること。回路のインダクタンス成分を低減するために、キャパシタンス成分も持たせることが考えられます。
他のスイッチング素子にも起こり得ることですが、CMOSも同様に注意する必要があります。
CMOSの動的消費電力
動的消費電力とは、下記2項目を合わせたものです。
- 入力電圧が0V➡1V➡0Vのパルス波を周波数\(f\)で1秒間入力したとき、CMOSで充放電する電力。
- PMOSとNMOSの導通関係が切り替わるときに発生する貫通電流による電力
まず1.について詳しく見ていきます。
パルス波が1回の消費電力を見ていきましょう。
電源からの供給電力に対し、PMOS、NMOSで消費する電力を考える。
- 0Vのとき:PMOSが導通しているのでコンデンサに静電エネルギー\(U=\dfrac{1}{2}CV_{c}^{2}\)が蓄えられる。
電源からの供給電力は\(P=QV_{c}=CV_{c}^{2}\)のため、その差半分はPMOSで消費される。 - 1Vのとき、NMOSが導通しているので、コンデンサからGNDへ静電エネルギー\(U=\dfrac{1}{2}CV_{c}^{2}\)を放出する。
- 0Vのとき、1.に戻る(2周期目)
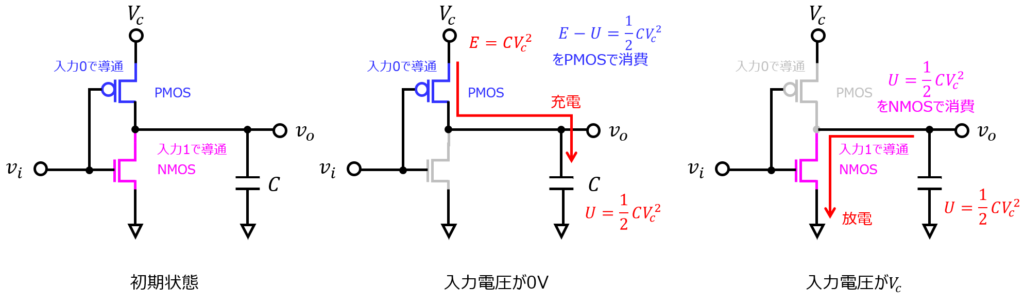
よって、1周期で\(CV_{c}^{2}\)の電力を消費します。
周波数\(f\)と、スイッチング確率\(\eta\)をかけると、1秒間の消費電力は下記になります。
\begin{aligned}P_{1}=CV_{c}^{2}f\cdot \eta\end{aligned}
なお、ゲートの数を\(N\)個とすると、下記になります。
\begin{aligned}P_{1}=\sum ^{N}_{i=1}CV_{c}^{2}f\cdot \eta\end{aligned}
貫流電流による発生する消費電力は、(2)の考え方を用います。
スイッチングにより、両方導通している時間が\(T\)で、1秒間のスイッチング回数分損失が起きますので、下記式で表すことができます。
\begin{aligned}P_{2}=\eta \int _{0}^{T}I\cdot \overline{v_{i}}fdt\end{aligned}
同じく、ゲートの数を\(N\)個とすると、下記になります。
\begin{aligned}P_{2}=\sum ^{N}_{i=1}\eta \int _{0}^{T}I\cdot \overline{v_{i}}fdt\end{aligned}
結局、動的消費電力は\(P_{1}+P_{2}\)になります。
動的消費電力を低減するための手法
(1)(2)式のパラメータをなるべく下げることを考えます。
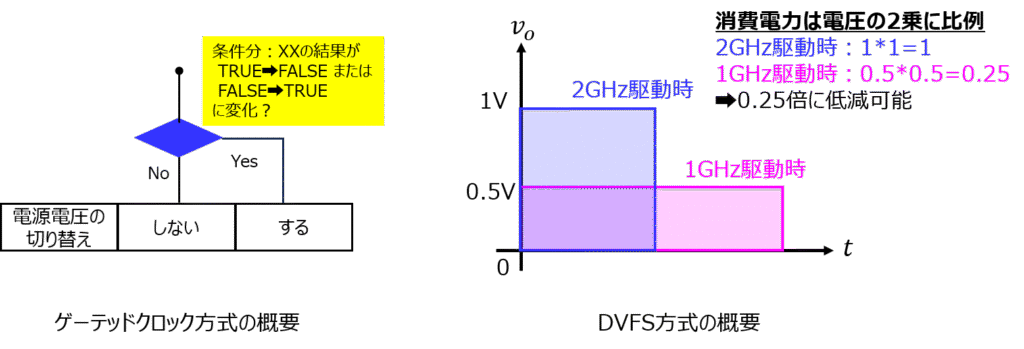
- ゲーテッドクロック方式:毎周期入力電圧を切り替えるのではなく、必要な時だけ切り替えることで、発生確率\(\eta\)を低減する
- DVFS方式:処理負荷が軽いときは、電圧周波数を下げる
1.については、プログラミングのif文で考えると分かりやすいです。
if:条件式=TRUEの処理を実施しているときは、TRUEの処理向けのCMOS回路を動作させる。FALSEのときは、FALSE用の動作を保持しておき、必要な時だけ切り替える動かし方をします。
このようにすることで、スイッチング確率\(\eta\)が下がり、消費電力を低減できます。
2.については、そのままです。
(1)(2)式ともに、消費電力は周波数の1乗と電源電圧の2乗に比例します。それぞれを低負荷の時は下げることで、演算処理に実害無く消費電力を低減することができます。
最後に
本問は、神戸大、京都工芸繊維大学の院試でよく出題されます。
両者の大学院のうち一つでも考えている方は、是非マスターしましょう。



