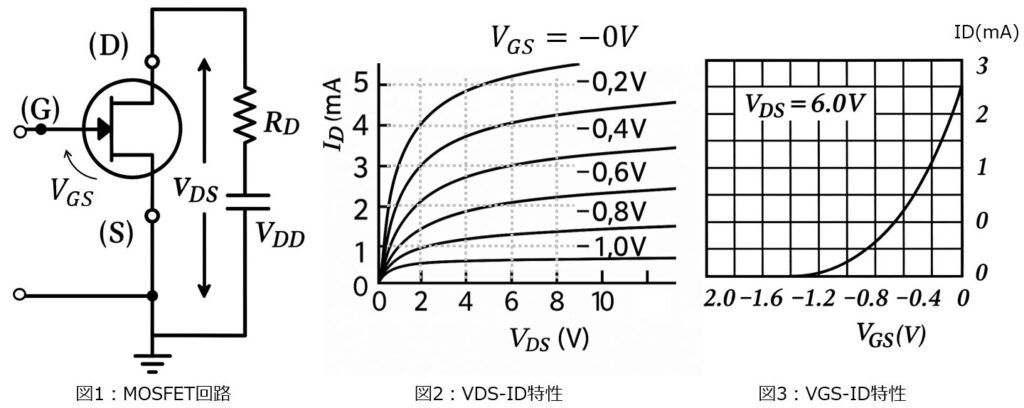
下記のMOSFET回路を考える。入出力特性は下記の図で与えられる。\(R_{D}=2.5kΩ,V_{DD}=10V\)とし、下記の問に答えよ。
(1)ドレインに流れる電流を\(I_{D}\)とする。\(V_{DS}\)と\(I_{D}\)の関係式を導け。
(2)動作点における\(V_{GS}\)を-0.6Vとしたとき、\(V_{DS}\)を求めよ。また、ドレイン抵抗\(r_{D}\)を求めよ。
(3)動作点を\(V_{DS}=6.0V\)としたとき、\(V_{D},V_{GS}\)を求めよ。
はじめに
MOSFETの特性は、過去の記事で多く説明してきました。出題範囲の9割方網羅できている(と思いたい)ですが、紹介してきた問題は微小信号等価回路を用いて解くことが多かったです。
一方で、本問のようにグラフの特性を利用し、非線形素子のまま解く問題も出題されることがあります。経験さえしていれば問題無く得点できますので、本問で練習しましょう。
なお、MOSFETだけでなく、バイポーラトランジスタを用いた場合でも同様の問題が出題されることがあります。
解答例
(1)\(V_{DS}\)と\(I_{D}\)の関係式
非線形素子(MOSFET)における\(V_{GS}\)、\(V_{DS}\)の具体的な値はこの時点で分かりません。よって、未知数として回路方程式(電圧則)の立式を優先します。
\begin{aligned}V_{DD}=R_{D}I_{D}+V_{DS}\end{aligned}
\(R_{D}=2.5kΩ,V_{DD}=10V\)だから、上式に代入すると
\begin{aligned}10=2.5*10^{3}I_{D}+V_{DS}\end{aligned}
\begin{aligned}I_{D}=4.0*10^{-3}-4.0*10^{-4}V_{DS}\end{aligned}
(2)動作点\(V_{GS}=-0.6V\)における\(V_{DS}\)
(1)で求めた関係式と問題で与えられた図2の条件が一致する点が解になります。図2のグラフは非線形であるため、式として与えられていないです。このため、グラフ上に(1)の結果をプロットし、交点を図式的に求める方法で解を求めます。
(3)式を図2にプロットすると下記のようになる。

\(V_{GS}=-0.6V\)との交点を求めると、\(V_{DS}=5V\)。
ドレイン抵抗については、\(r_{D}=\frac{\Delta V_{DS}}{\Delta I_{D}}\)で表される。\(V_{GS}=-0.4V\)のとき、\(V_{DS}=4V,8V\)の動作点\(I_{D}=1.75,2.25mA\)に注目して
\begin{aligned}V_{DS}&=\dfrac{8-4}{(2.25-1.75)*10^{-3}} \\ &=8kΩ\end{aligned}
補足
(4)式は、一定の区間を取った平均値のドレイン抵抗になります。\(V_{DS}\)と\(I_{D}\)の関係式が与えられている場合は、その式を微分した方が正確なドレイン抵抗\(r_{D}\)が求められます。
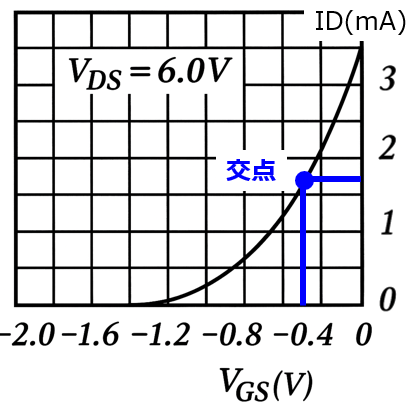
(3)動作点における\(I_{D},V_{GS}\)
\(I_{D}\)と\(V_{GS}\)の関係を表しているのは図3です。よって、前問から\(I_{D}\)を求めてこれを図3にプロットすることで\(V_{GS}\)を求めます。
(3)式に\(V_{DS}=6.0V\)を代入し
\begin{aligned}I_{D}=1.6mA\end{aligned}
図1の特性曲線において、\(I_{D}=1.6mA\)の点をプロットすると交点は\(V_{GS}=-0.5V\)
最後に
非線形素子を微小信号等価回路に近似しない場合、素子の特性が与えられる問題が多いです。上記のように、関係式をグラフに図示することで解決できます。