トランジスタ、MOSFETを使用した差動増幅回路

電子回路

2024.06.082024.12.19

問題

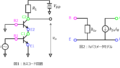
下記の図1,3の差動増幅回路について考える。

(1)小信号等価回路を示せ。
(2)差動利得\(K_{1}=\dfrac{v_{o1}-v_{o2}}{v_{i1}-v_{i2}}\)を求めよ。
(3)同相利得\(K_{2}=\dfrac{v_{o1}+v_{o2}}{v_{i1}+v_{i2}}\)を求めよ。

ただし、図1の回路には図2のモデル、図3の回路には図4のモデルを適用せよ。
また、トランジスタ、MOSFETのパラメータ\(h_{ie},h_{fe},g_{m}\)は各素子区別せず、共通とせよ。

差動増幅回路とは
解答例
最後に

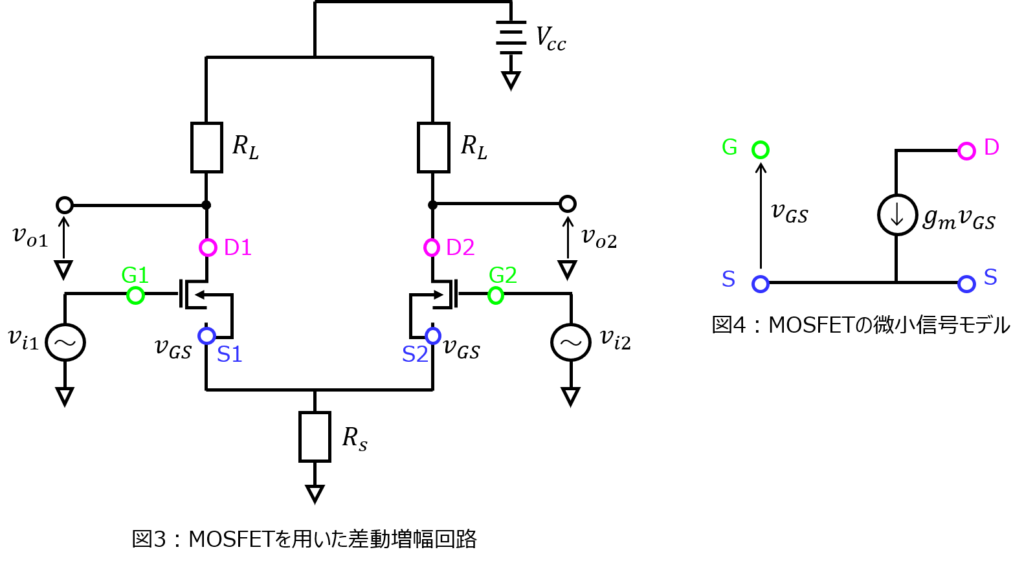
差動増幅回路とは

図1,3のように、同じ回路を並列に接続し、異なる電圧源を入力。その電圧差を増幅する回路です。(電圧を足し合わせた場合の利得を考える場合は、同相利得と呼ばれます。)

オペアンプを使用した場合もありますが、本問では、トランジスタとMOSFETを対象にします。

トランジスタとMOSFETの動作概要は、下記のページにまとめています。

解答例

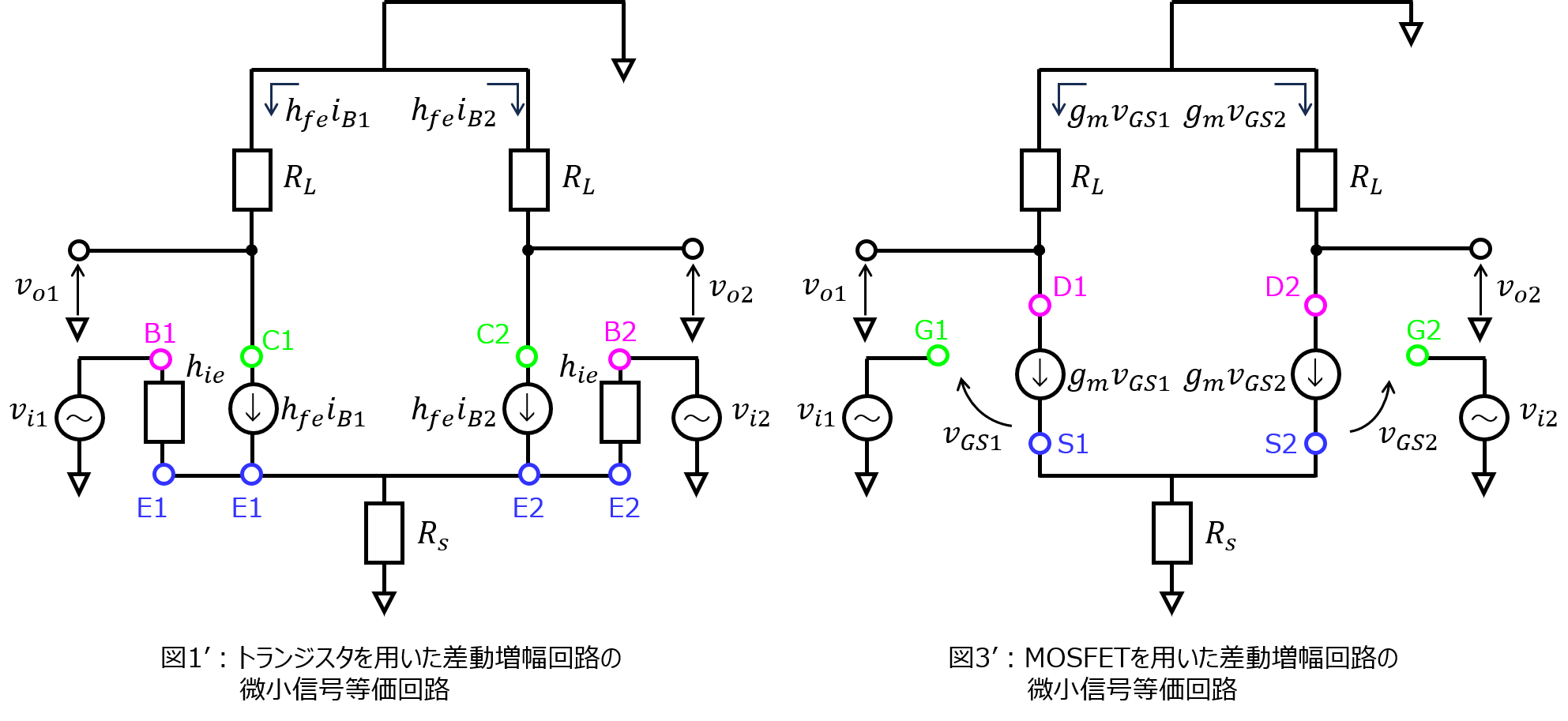
(1)微小信号等価回路の図示

これは今までの記事で沢山解説しています。トランジスタ、MOSFETが複数になろうと、やることは変わりません。非線形素子を与えられた近似モデルに置き換えることに集中します。

トランジスタの場合を下記の図1’、MOSFETの場合を図3’に示します。

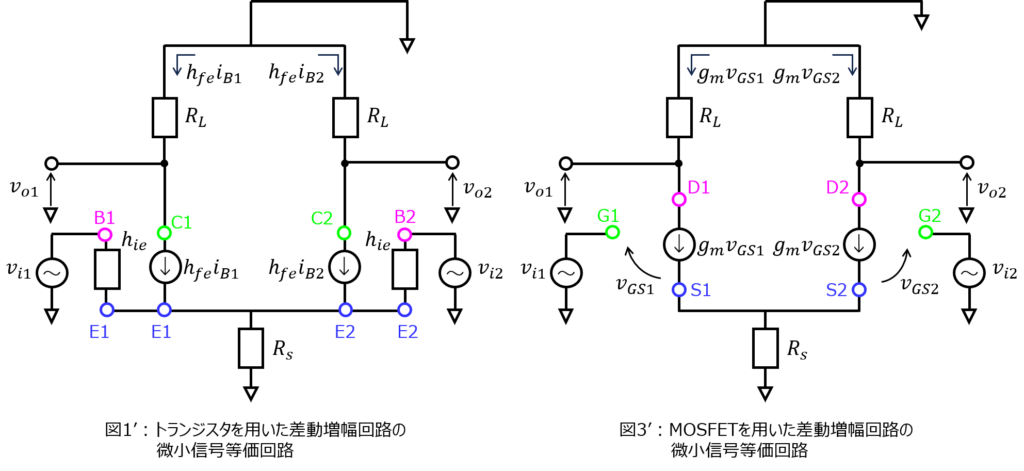
(2)(3)差動利得、同相利得

別々の利得ですが、やることは変わりません。

(1)で求めた小信号等価回路を用いて回路方程式を立てて、それぞれの定義式に基づいて計算していきます。

トランジスタの場合

下記の回路方程式になる。

\begin{cases} v_{i1}=hi_{e}i_{B1}+R_{s}{ \left( 1+h_{fe}\right) i_{B1} + \left( 1+h_{fe}\right) i_{B2}} \\ v_{i2}=h_{ie}i_{B2}+R_{s}{ \left( 1+h_{fe}\right) i_{B1} + \left( 1+h_{fe}\right) i_{B2}} \\ v_{o1}=-R_{L}f_{fe}i_{B1} \\ v_{o2}=-R_{L}f_{fe}i_{B2} \end{cases}

これを用いて、求める差動利得\(K_{1}\)は

\begin{aligned}K_{1}=\dfrac{v_{o1}-v_{o2}}{v_{i1}-v_{i2}}&=\dfrac{-R_{L}h_{fe}(i_{B1}-i_{B2})}{h_{ie}(i_{B1}-i_{B2})} \\ &=-\dfrac{R_{L}h_{fe}}{h_{ie}} \end{aligned}

次に、同相利得\(K_{2}\)は

\begin{aligned}K_{2}=\dfrac{v_{o1}+v_{o2}}{v_{i1}+v_{i2}}&=\dfrac{-R_{L}h_{fe}(i_{B1}+i_{B2})}{h_{ie}(i_{B1}+i_{B2})+2R_{s}(1+h_{fe})(i_{B1}+i_{B2})} \\ &=-\dfrac{R_{L}h_{fe}}{h_{ie}+2R_{s}(1+h_{fe})} \end{aligned}

MOSFETの場合

下記の回路方程式になる。

\begin{cases} v_{i1}=v_{GS1}+R_{s}g_{m}(v_{GS1}+v_{GS2}) \\ v_{i2}=v_{GS2}+R_{s}g_{m}(v_{GS1}+v_{GS2}) \\ v_{o1}=-R_{L}g_{m}v_{GS1} \\ v_{o2}=-R_{L}g_{m}v_{GS2} \end{cases}

これを用いて、求める差動利得\(K_{1}\)は

\begin{aligned}K_{1}=\dfrac{v_{o1}-v_{o2}}{v_{i1}-v_{i2}}&=\dfrac{-R_{L}g_{m}(v_{GS1}-v_{GS2})}{(v_{GS1}-v_{GS2})} \\ &=-R_{L}g_{m}\end{aligned}

次に、同相利得\(K_{2}\)は

\begin{aligned}K_{2}=\dfrac{v_{o1}+v_{o2}}{v_{i1}+v_{i2}}&=\dfrac{-R_{L}g_{m}(v_{GS1}+v_{GS2})}{(2R_{s}g_{m}+1)(v_{GS1}+v_{GS2})} \\ &=-\dfrac{R_{L}g_{m}}{2R_{s}g_{m}+1} \end{aligned}