電子回路の発振条件の考え方

はじめに
発振の原理
ナイキスト線図から見る発振条件と周波数条件
最後に

はじめに

電気電子回路には、「発振」という現象が存在します。

電気回路の場合は、インピーダンスの虚部成分が0になる(角)周波数を発振条件と言われることが多いです。

このとき、電圧源と負荷(インピーダンス)の位相が一致しますので、力率=1になります。(有効電力を大きく取り出せる)

一方で、電子回路の場合はどのようなイメージをお持ちでしょうか。

一般的に、入力電圧が0でも出力電圧が0にならない、増幅し続ける現象を指しています。

どういうことなのか、下記で考えていきましょう。

発振の原理

発振条件の定義とは、下記になります。

発振条件の定義

ループ利得AHが下記の2つの条件を満たすこと。

発振条件： $R e (A H) > 1$ (振幅条件とも言われる。)
周波数条件： $I m (A H) = 0$

なぜ、このような条件になるのか、下記で説明していきます。

原理をモデルで理解する

下記のようなオペアンプを用いた正帰還回路を考えます。(Aはオペアンプの電圧利得で、Hは帰還率)

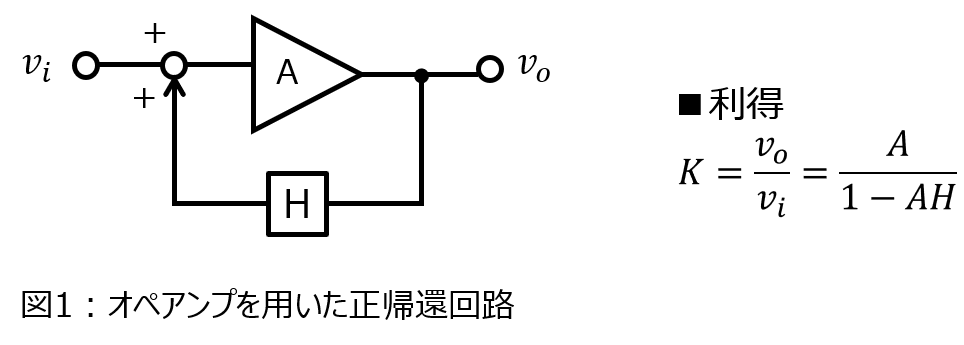
出力電圧 $v_{o}$ は、入力電圧 $v_{i}$ を用いて下記のように表されます。

$\begin{matrix} (1) & \begin{array}{r} v_{o} = A (v_{i} + H v_{o}) \end{array} \end{matrix}$

これより、回路全体の利得Kは下記になります。

$\begin{matrix} (2) & \begin{array}{r} K = \frac{v_{o}}{v_{i}} = \frac{A}{1 - A H} \end{array} \end{matrix}$

上式が発振条件を考えるうえでのカギになります。

正帰還回路のループ利得が $A H = 1$ のとき、回路全体の利得は $G = \infty$ になります。

このとき、入力電圧を与えなくとも出力電圧 $v_{o}$ が存在します。これが発振回路の原理になります。

発振条件

前節の回路において、ループ利得 $A H > 1$ である場合を考えます。

分かりやすくするため、 $A = 3, H = 0.5$ としましょう。

このとき、単位インパルス関数を $t = 0$ で入力します。出力電圧は、 $A = 3$ より $v_{o} = 3$ になります。

次に、 $t = 1$ のときを考えます。帰還率 $H = 0.5$ で、入力電圧は0なので、 $t = 0$ の出力電圧に帰還率をかけた $3 * 0.5 = 1.5$ が増幅器に入ります。

増幅器でゲイン3倍するので、 $1.5 * 3 = 4.5 V$ が出力されます。t=0と比較して1.5V増えました。

このように、時間を追うごとに出力電圧が増えていきます。これを発振条件と言います。(簡単化のために、t=0,1など離散的に時間を考えていますが、アナログ回路なら連続的に出力電圧が増えていきます。)

発振条件下でも、出力電圧は飽和する。

前節の説明により、発振条件が成立するとき出力電圧は増加していきます。

このまま行くと、出力電圧が発散しそうに見えますが、実際そうはなりません。増幅器(オペアンプ)にかかる電源電圧の制約からです。

院試では、省略されていることが多いですが、増幅器には外部電源が繋がっています。増幅器自体に電圧(エネルギー)を増加させる効果はありません。(エネルギー保存則の観点からもあり得ません。)

あくまでも、外部電源から供給する電圧の範囲で出力電圧を増幅させます。

ですので、外部電源電圧が10Vの場合、出力電圧は10Vで飽和します。

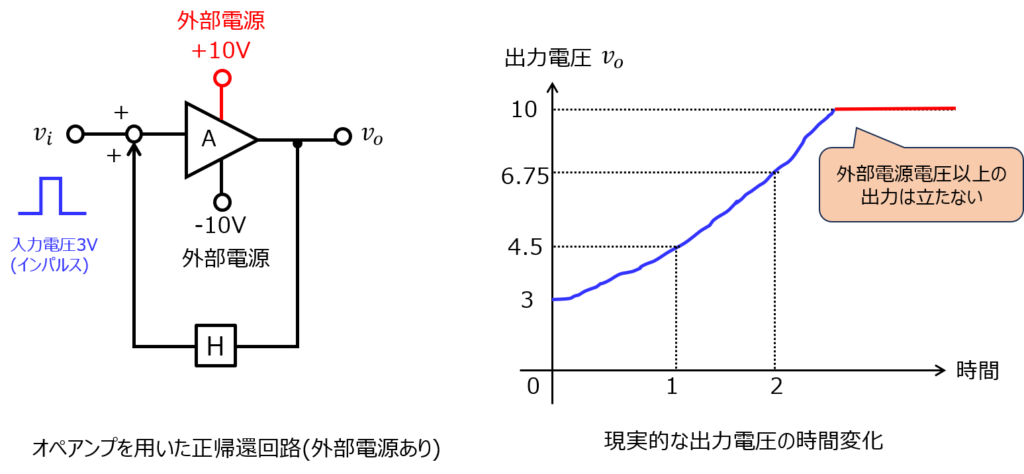
このとき、入力電圧と出力電圧が同じになるため、ループ利得 $A H = 1$ になります。

このように、発振条件 $A H > 1$ が成立していても最終的には $A H = 1$ となることから、発振条件を $A H = 1$ と初めから説明している専門書もあります。

ナイキスト線図から見る発振条件と周波数条件

(2)式より、系の利得Kが求まりました。これは、制御工学的には伝達関数 $G$ とみることもできます。

前章では、簡単化のため正帰還としていましたが、負帰還として、一巡伝達関数 $- A H$ を考えます。

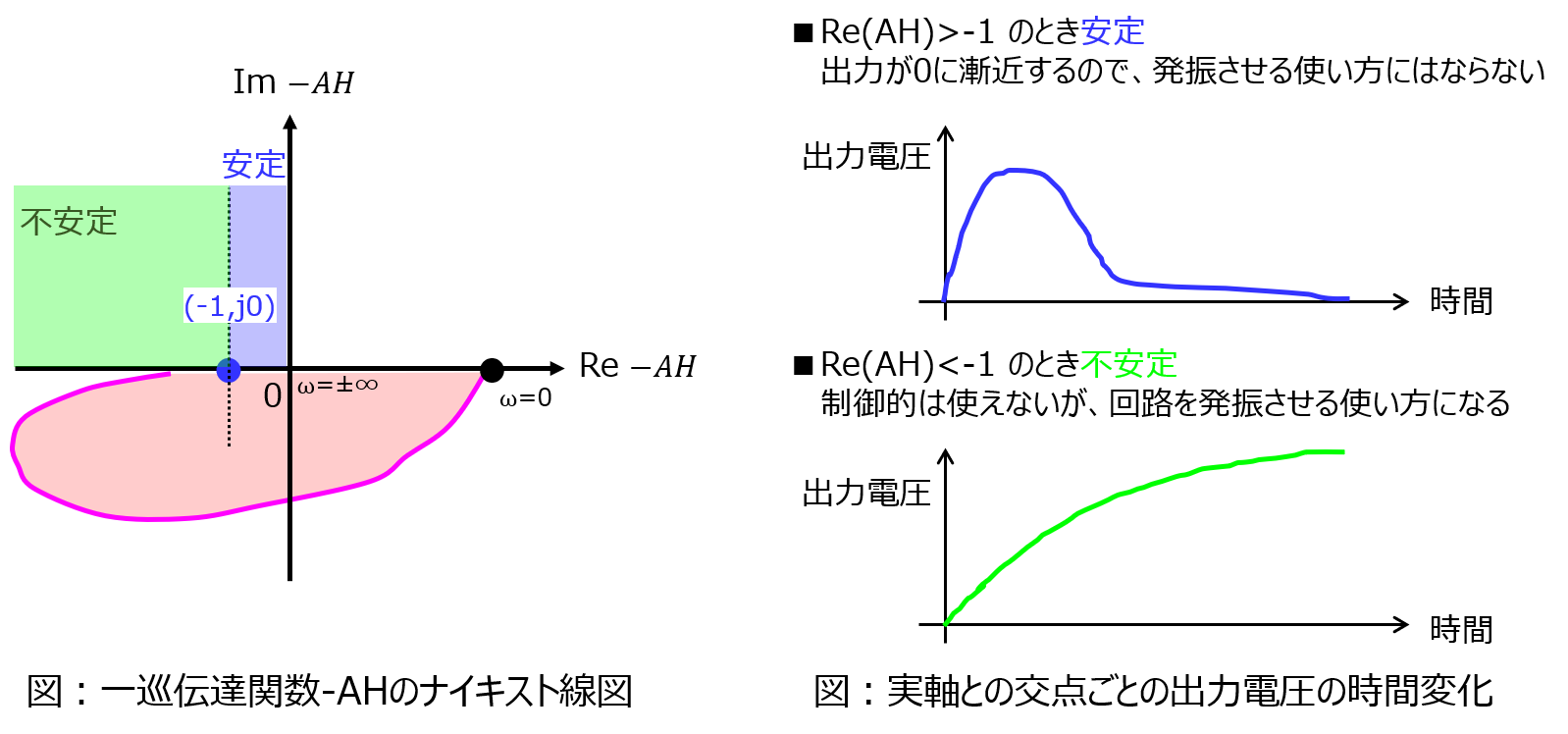
これをナイキスト線図としてプロットすると、下記のような形になります。

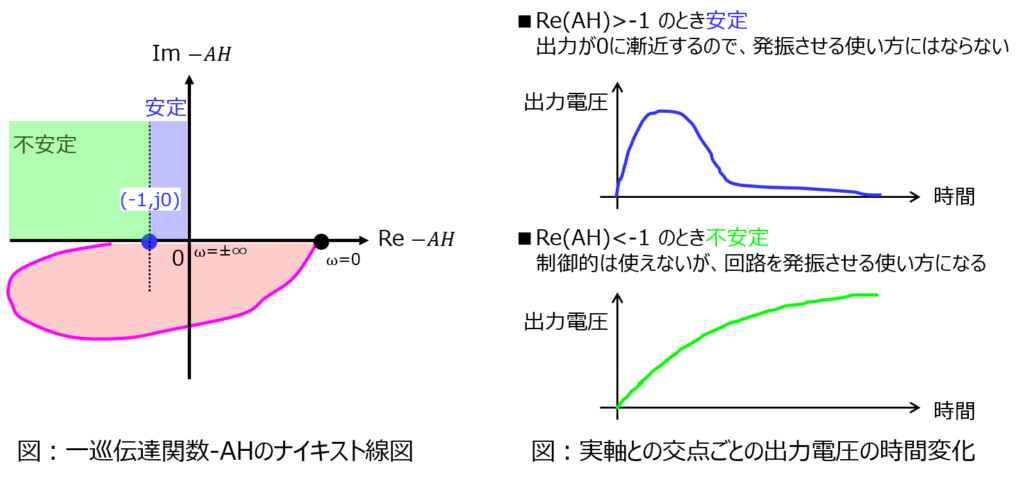
制御の問題を解くときは、安定になる条件を求めることが殆どで実軸と交わる点が $R e (A H) < - 1$ となれば良かったです。

しかし、発振の場合は逆です。出力が発散しなければならないので、 $R e (A H) > - 1$ となる必要があります。

前章で考えた $A H > 1$ と整合性が取れました。

なお、実軸に交わる点を考えるため、この時の虚部は0になります。回路が発振するためには、この条件も必要となるため

$\begin{matrix} (3) & \begin{array}{r} I m (A H) = 0 \end{array} \end{matrix}$

も同様に条件に存在します。(周波数条件)

これは、入力電圧と出力電圧が同じ位相であることを示しています。もし、位相がずれている場合、入力電圧と出力電圧が打ち消し合い、上手く増幅できないからですね。

問題を解いていく上での注意点

「発振条件」という言葉だけを聞くと、今までの説明からするに $R e (A H) > 1$ になる条件だけ求めると良いように感じます。

しかしながら、大学によっては周波数条件 $I m (A H) = 0$ も合わせて「発振条件」と指導をされているところもあります。( $R e (A H) > 1$ は、「振幅条件」と別の言葉に置き換えられています。)

院試問題を解いていく上では、安全のために周波数条件も求めておくと良いかもしれません。

最後に

本記事の考え方を軸に、発振回路の問題を解いていきます。コルピッツ発振回路やハートレー発振回路などがあります。

これらの発振条件、周波数条件を次回以降の記事で紹介していきます。