\(\boldsymbol{E}=E_{o}\exp(j \omega t)\widehat{\boldsymbol{x}}\)で表される電場が存在する。これが、導電率\(\sigma\)、誘電率\(\varepsilon\)の導体内を伝搬するとき、次の問いに答えよ。
(1)伝導電流密度\(\boldsymbol{i}\)と変位電流密度\(\boldsymbol{i_{D}}\)の大きさをそれぞれ求めよ。また、両者の位相差についても考えよ。
(2)金属内、真空中それぞれを伝搬するとき、伝導電流、変位電流のどちらが支配的であるかを答えよ。
(3)電磁誘導の法則を用いて、電場に関する電信方程式を導出せよ。
ただし、\(rot(rot \boldsymbol{A})=grad(div \boldsymbol{A})- \Delta \boldsymbol{A}\)を利用して良い。
(4)(3)で求めた電信方程式に対し、(2)の結果を用いて近似を行い、金属導体中の拡散方程式を求めよ。
(5)\(\boldsymbol{E}=E(x)\exp(j \omega t)\widehat{\boldsymbol{x}}\)とする。\(E(x)=E_{o}\exp(-ax)\)を仮定し、(4)で求めた拡散方程式を利用し、導体中の電場分布\(E(x)\)を求めよ。(aは未知数)
ただし、\(x<0\)の範囲は真空とし、\(x>0\)の範囲を金属導体とする。
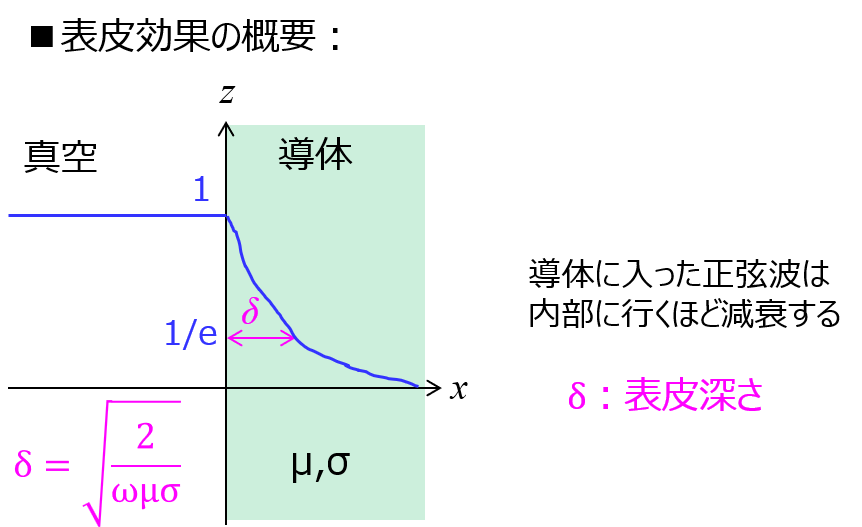
(6)(5)で求められた現象を表皮効果という。\(E(x)\)の絶対値を取り、表皮深さ\(\delta\)を求めよ。
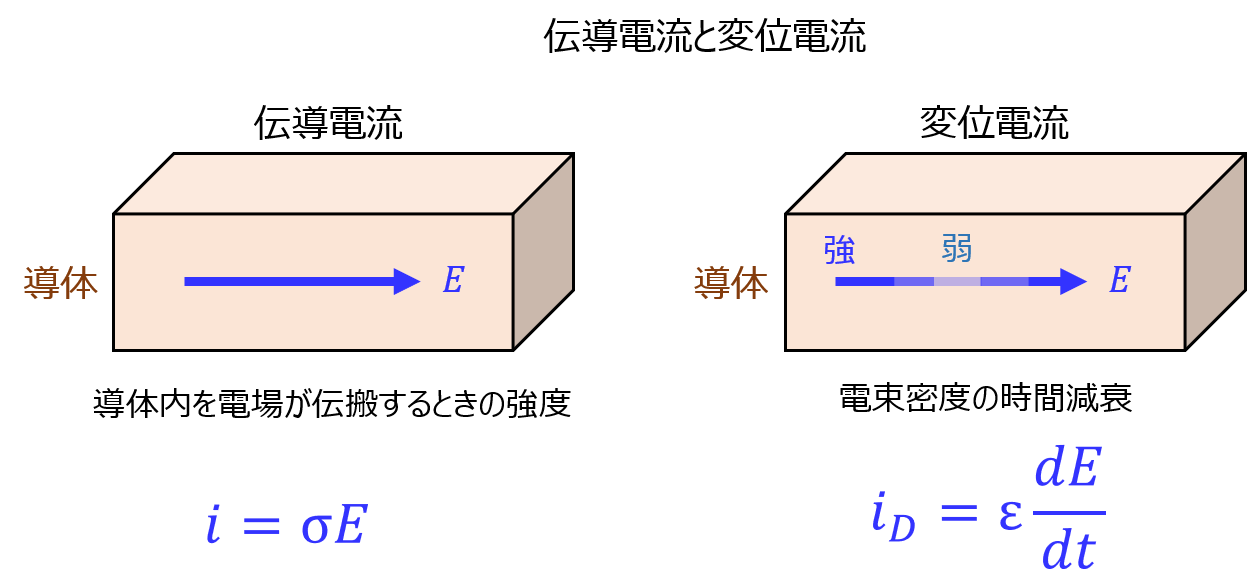
伝導電流と変位電流
伝導電流とは
導体中を流れる電流のことです。\(\boldsymbol{i}=\sigma \boldsymbol{E}\)と、電場に導電率をかけた結果にあたります。
変位電流とは
電束密度の時間変化を言います。
ある地点の電場が時間変化する=伝導電流以外にも電流は流れている。という解釈です。
よく、コンデンサを例として、極板から出てくる電荷が変位電流だという説明があります。初学者には分かりやすいと言えども、管理人としてはイマイチな説明と考えます。
程度の違いはあれど、コンデンサ以外の導体においても誘電率\(\varepsilon\)が0でない限り変位電流は存在します。
1.電流連続の式を時間変化する場に対しても成立させるため、電束密度の時間微分項を形式的に追加したらうまくいった。
2.伝導電流と区別するために、変位電流と名付けた。
くらいの理解で、実学重視の工学部なら良いと思います。(もし、万人に分かりやすいイメージがあれば教えてください。)
解答例
(1)伝導電流と変位電流の算出
伝導電流密度について、前章の説明より
\begin{aligned}|\boldsymbol{i}|=\sigma E_{o}\end{aligned}
変位電流密度について、電束密度の時間微分なので
\begin{aligned}|\boldsymbol{i_{d}}|=\left| \dfrac{d\boldsymbol{D}}{dt} \right|=\varepsilon \omega E_{o}\end{aligned}
伝導電流に虚部は無い。(実部のみ)
変位電流密度は時間微分しているので実部は無い。(虚部のみ)
よって、両者の位相差は\(\frac{\pi}{2}\)。
(2)金属導体/真空中での伝導電流、変位電流
伝導電流と変位電流の大小関係を考える。(1)式と(2)式の比を取ればよく
\begin{aligned}\left|\dfrac{\boldsymbol{i_{D}}}{\boldsymbol{i}}\right|=\dfrac{\omega \varepsilon}{\sigma}\end{aligned}
金属導体のとき、導電率\(\sigma \fallingdotseq 10^{7}\)で、誘電率\(\varepsilon \fallingdotseq 10^{-10}\)、ギガヘルツ帯の電場でも、\(\omega \fallingdotseq 10^{9}\)である。
よって、伝導電流が支配的。
真空中のとき、導電率\(\sigma \fallingdotseq 0\)と近似できるため、変位電流が支配的。
(3)電信方程式の導出
この問題は、東北大でよく出てきます。
電磁誘導の法則\(rot \boldsymbol{E}=-\dfrac{\partial \boldsymbol{B}}{\partial t}\)に対し、回転(rot)を取る。
一般的に、あるベクトル場の回転を取った勾配は0なので、\(grad (div \boldsymbol{A})=0\)を利用し
\begin{aligned}rot(rot \boldsymbol{E})&=\\ – \Delta \boldsymbol{E}&=-\sigma\mu\dfrac{\partial \boldsymbol{E}}{\partial \boldsymbol{t}}-\varepsilon\mu \dfrac{\partial^{2} \boldsymbol{E}}{\partial \boldsymbol{t^{2}}} \\ \Delta \boldsymbol{E}&=\sigma\mu\dfrac{\partial \boldsymbol{E}}{\partial \boldsymbol{t}}+\varepsilon\mu \dfrac{\partial^{2} \boldsymbol{E}}{\partial \boldsymbol{t^{2}}} \end{aligned}
これが、電場に関する電信方程式である。
(4)金属導体中の拡散方程式
(2)より、金属導体中の導電率は、\(\sigma\)は\(10^{8}\)。
誘電率は\(\varepsilon\fallingdotseq10^{-10}\)。透磁率は\(\mu\fallingdotseq10^{-3}\)。よって、導電率\(\sigma\)が支配的。
(4)式の右辺第2項は無視できるので
\begin{aligned}\Delta \boldsymbol{E}&=\sigma\mu\dfrac{\partial \boldsymbol{E}}{\partial t}\end{aligned}
これが、求める拡散方程式である。
(5)導体中の電場分布 (表皮効果)
(4)で求められた拡散方程式に\(\boldsymbol{E}=E(x)\exp(j \omega t)\widehat{\boldsymbol{x}}\)を代入する。
\begin{aligned}\dfrac{\partial^{2}}{\partial x^{2}}E(x)=j \omega \mu \sigma E(x)\end{aligned}
\(E(x)=E_{o}exp(-ax)\)を(6)に代入
\begin{aligned}a^{2}=j\omega \mu \sigma \\ a=\sqrt{j\omega \mu \sigma}\end{aligned}
\(\sqrt{j}=\sqrt{\exp\left(\dfrac{\pi}{2}\right)}=\exp\left(\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}+\dfrac{j}{\sqrt{2}}\)なので
\begin{aligned}a=\sqrt{\dfrac{\omega \mu \sigma}{2}}+j\sqrt{\dfrac{\omega \mu \sigma}{2}}\end{aligned}
以上より、電場分布\begin{aligned}E(x)=E_{o}\exp\left(-\left(\sqrt{\dfrac{\omega \mu \sigma}{2}}+j\sqrt{\dfrac{\omega \mu \sigma}{2}}\right) x \right)\end{aligned}が得られた。
(6)表皮深さについて
(9)式について、\(\exp\)項の内部が-1になる\(x\)が表皮深さである。
\(E(x)\)の絶対値を考える。
exp()項の虚部は、絶対値を取ると1になる。実部だけに注目すれば良く
\begin{aligned}|E(x)|=E_{o}\exp\left(-\sqrt{\dfrac{\omega \mu \sigma}{2}}x\right)\end{aligned}
よって、求める表皮深さは
\begin{aligned}\delta = \sqrt{\dfrac{2}{\omega \mu \sigma}}\end{aligned}
補足:表皮効果を低減する手法
(9)式より、下記の条件のとき、表皮深さが短くなり、導体表面にしか電流が流れなくなります。
- 動作周波数が大きい
- 透磁率が大きい
- 導電率が大きい
動作周波数について、低くすれば良いですが、使用する機器の特性上変えられないことがあります。
透磁率、導電率について、小さい導体を選べば良い。と言いたいところですが、そうなると抵抗値が大きくなり、ジュール損失が大きくなります。
結局、3つのパラメータをどれか1つでも改善することは難しいです。
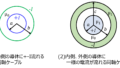
代案として、導体自体の形状を変える方法があります。
太い導線を1本よりも、細かい導線を何本もまとめた方が導体全体の表面積が増えます。
よって、電流が流れる範囲が増えます。(下図)
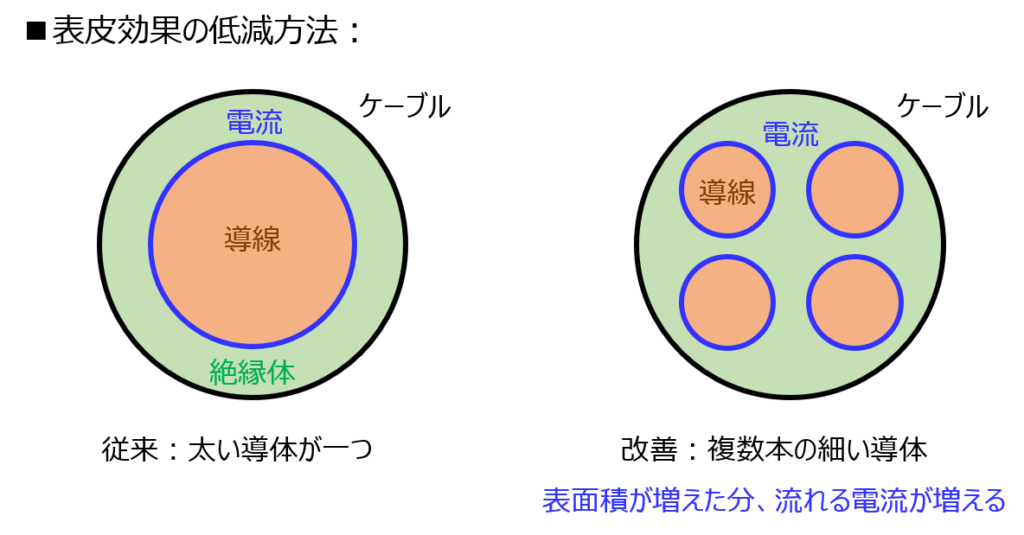
また、渦電流損を低減するために、導線は磁場と鎖交しにくい形状にすると良いです。(丸形など)
最後に
伝導電流と変位電流の関係から表皮効果を導出する流れは院試で良く出てきます。
微分方程式の知識も出てきます。院試で選択しないからと言って全くの知識なしは本問を解くうえで厳しいです。
本記事で紹介する流れを自分のものにし、出題された際は得点源にできると幸いです。