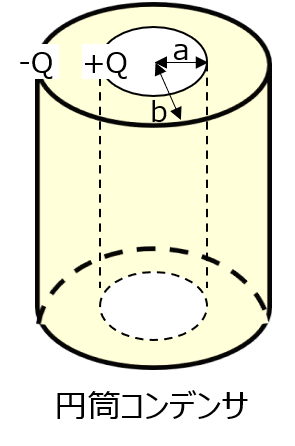
下記の図のように、内径\(a\)、外径\(b\)の円筒コンデンサがある。内径に電荷\(Q\)、外径に電荷\(-Q\)を与えるとき、下記の問いに答えよ。
(1)単位長さあたりの静電容量を求めよ。
(2)本コンデンサで蓄えられる静電エネルギーを、遠隔作用、近接作用、二つの立場から求めよ。そして、両者が等しいことを確認せよ。
遠隔作用と近接作用の違い
2つの物体における相互作用が
- 場を介さずに直接作用し合う(遠隔作用)
- 場を介して間接的に作用し合う(近接作用)
例えば、距離\(r\)離れた二つの電荷\(q_{1},q_{2}\)を考えます。2つの電荷に働く力を遠隔作用、近接作用それぞれの立場で考えます。
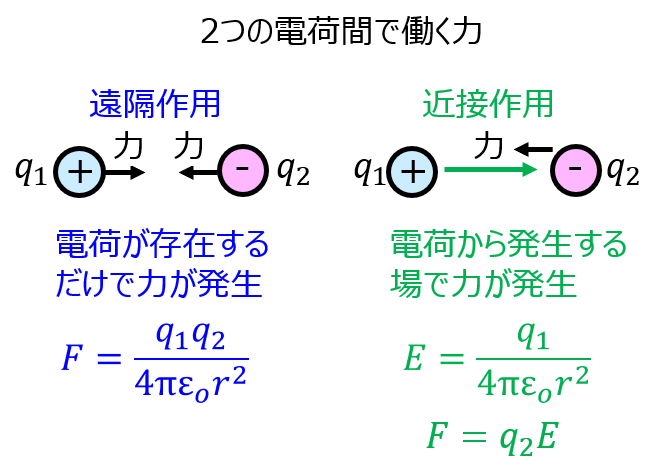
遠隔作用の場合
それぞれの物体に働く力は、クーロンの法則により
\begin{aligned}F=\dfrac{q_{1}q_{2}}{4 \pi \varepsilon_{o}r^{2}}\end{aligned}
であることが経験則的に分かっています。上式だけ見ると、電荷が存在しているだけで、間に何も無くとも二つの物体に力を及ぼしていることが分かります。
これを遠隔作用と言います。
近接作用の場合
遠隔作用では、電荷が存在すればそれだけで力が発生する視点で説明しました。しかし、実際はそうなのでしょうか。
厳密には、電荷\(q_{1}\)から発生する電場
\begin{aligned}E=\dfrac{q_{1}}{4 \pi \varepsilon_{o} r^{2}}\end{aligned}
が電荷\(q_{2}\)に届き、力\(F=q_{2}E\)が作用することからクーロン力が発生している見方ができます。
結果は(1)式と等しいですが、解釈の内容からして違います。
近年の電磁気学における解釈
院試問題を解いていると、電場を用いて系の特徴を考えている問題が多いです。このことから、近接作用の立場を取っています。
もし、遠隔作用的立場に立った際は、下記の説明を付けることができないです。
- 二つの物体を置いた時、瞬間的に力を及ぼし合う。
実際はそうではないです。電磁波の光速は\(3.0*10^{8}[m/s]\)と極めて速いですが、何kmも離れている地点に対し入射したとき、どうしてもタイムラグが発生します。
この実験結果が、遠隔作用として見た時に発生する決定的な矛盾となります。よって、近年では近接作用の立場に立ち、様々な電磁気学知見に基づいた研究がなされています。
補足
とは言え、遠隔作用の考えは全く使えないわけでは無いです。少なくとも、近接作用で求めた解に対しての妥当性を、遠隔作用の解釈と一致するかで確かめる。という使い方ができます。
下記では、本記事の冒頭で紹介した問題を用いて、それぞれの立場で答えを導いていきます。
解答例
(1)コンデンサの静電容量
これは(2)を行うための準備運動です。大したことはしないので、結果だけの確認でも良いかもしれません。
まず電場を求める。a<r<bにおいて、ガウスの法則より、円筒状の閉曲面(単位体積相当)を取って
\begin{aligned}E=\dfrac{Q}{2 \pi \varepsilon_{o} r}\end{aligned}
これを区間[b,a]で積分して、内径と外径の電位差\(V\)は
\begin{aligned}V&=-\int^{a}_{b} \dfrac{Q}{2 \pi \varepsilon_{o} r} dr \\ &= \dfrac{Q}{2 \pi \varepsilon_{o}}{\log\dfrac{b}{a}}\end{aligned}
以上より、求める静電容量は、\(Q=CV\)より
\begin{aligned}C=\dfrac{ 2 \pi \varepsilon_{o}}{\log \dfrac{b}{a}}\end{aligned}
(2)静電エネルギー
遠隔作用に立ったとき
静電エネルギー\(U\)は、\(U=\dfrac{1}{2}QV\)
内径と外径の静電エネルギーをそれぞれ\(U_{1},U_{2}\)とする。外径の電位は0なので
\begin{cases}U_{1}=\dfrac{1}{2}\dfrac{Q^{2}}{4 \pi \varepsilon_{o}}\log\dfrac{b}{a} \\ U_{2}=0\end{cases}
だから、求める静電エネルギー\(U\)は
\begin{aligned}U&=U_{1}+U_{2} \\ &= \dfrac{Q^{2}}{4 \pi \varepsilon_{o}}\log\dfrac{b}{a} \end{aligned}
近接作用に立ったとき
a<r<bの静電エネルギー密度\(u=\dfrac{1}{2}\varepsilon_{o}E^{2}\)は
\begin{aligned}u=\dfrac{1}{2}\varepsilon_{o} \left ( \dfrac{Q}{2 \pi \varepsilon_{o} r} \right )^{2}\end{aligned}
これを体積分し、求める静電エネルギーは
\begin{aligned}U&=\dfrac{1}{2}\varepsilon_{o} \int^{b}_{a} \left ( \dfrac{Q}{2 \pi \varepsilon_{o} r} \right )^{2} 2 \pi r dr \\ &=\dfrac{Q^{2}}{4 \pi \varepsilon_{o}}\log\dfrac{b}{a} \end{aligned}
以上より、遠隔作用の場合と一致する。
最後に
遠隔作用、近接作用の違いは、電磁気学の教科書にてさらっと説明して終わりの内容になることが多いですが、実際に北大で出題されたことがありました。試験問題対策を急ぐあまり、説明問題に対しては手薄になってしまいがちですが、教科書を一読する時間は用意しましょう。