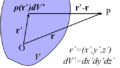
下記のように、真空中にy軸と平行な半径aの無限長円筒導体1が接地された無限平板導体から距離\(h\)(a<<h)の位置に存在する。下記の問いに答えよ。
(1)円柱導体1に単位長さあたり\(\lambda\)の電荷が一様に分布するとき、導体1に働く単位長さあたりの力の大きさを答えよ。
(2)導体1と無限平板導体間の静電容量を求めよ。
(3)導体1に直流電流を流す。表面のみを流れるとき、導体1の単位長さあたりの自己インダクタンスを求めよ。
(4)y軸と平行な別の半径aの無限長円筒導体2をx=d (a<<d),z=hに設置した。導体1に電圧\(V_{1}\)を印可したとき、導体2に誘導される電圧\(V_{2}\)を求めよ。
対地静電容量について
将来、電力系統工学を勉強するとき、フェランチ効果を理解するための背景知識に用います。
円筒導体が電荷を帯びている時、電場が発生します。電場は、電位が小さい箇所に向かって流れるため、電位0のアースに向かって流れます。
このような物理現象により、円筒導体と接地極には静電容量が発生している解釈ができます。
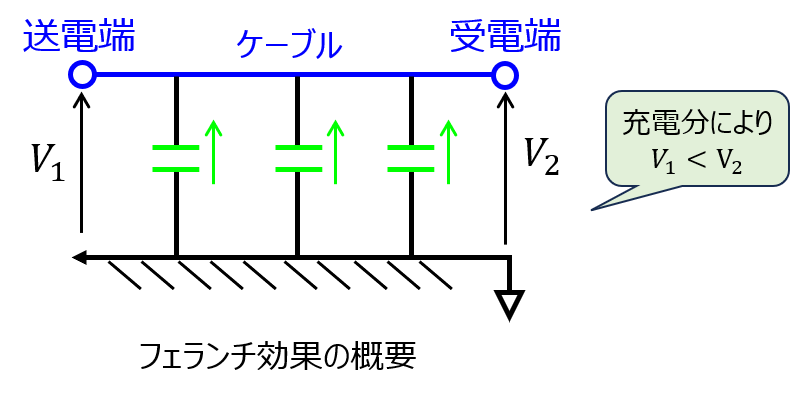
静電容量が発生すると、充電により電圧が発生しているとみなすことができます。よって、受電端が送電端よりも電圧が高くなる現象が発生します。これをフェランチ効果と言います。
本記事では、円筒導体とアースの間の静電容量に関する振る舞いを解説していきます。
対地静電容量の求め方
以前の記事で一度説明した鏡像法を利用します。アースと対称な位置に鏡像電荷を置き、両者から発生する電位、電場を求める方針に変わりありません。
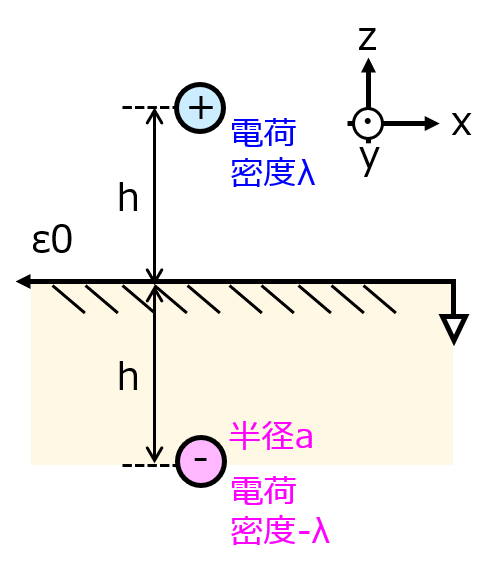
なお、無限長導体であるため、単位長さ辺りの電荷密度で考えます。
(1)導体1に働く力
鏡像電荷とのクーロンの法則を考えれば良い。真電荷と2hの距離が離れているので
\begin{aligned}F=\dfrac{\lambda^{2}}{4 \pi \varepsilon_{o} (2h)^{2}}=\dfrac{\lambda^{2}}{16 \pi \varepsilon_{o}h^{2}}\end{aligned}
(2)導体1と接地された平板間の静電容量
ガウスの法則より、半径\(z\)の円筒を取って
\begin{aligned}E(z)=\dfrac{\lambda}{2 \pi \varepsilon_{o}(h-z)}+\dfrac{\lambda}{2 \pi \varepsilon_{o}(h+z)}\end{aligned}
これより、導体1の電位は、平板が基準(電位0)。(a<<h)なので
\begin{aligned}V&=\int^{h-a}_{0}E(z)dz \\ &=\dfrac{\lambda}{2 \pi \varepsilon_{o}}\lbrack -\log(h-z) + \log(h+z) \rbrack ^{h-a}_{0} \\ &=\dfrac{\lambda}{2 \pi \varepsilon_{o}}\log\dfrac{2h-a}{a} \\ & \fallingdotseq \dfrac{\lambda}{2 \pi \varepsilon_{o}}\log\dfrac{2h}{a}\end{aligned}
したがって、求める静電容量\(C\)は、\(\lambda=CV\)の関係により
\begin{aligned}C=\dfrac{2 \pi \varepsilon_{o}}{\log\dfrac{2h}{a}}\end{aligned}
(3)インダクタンスの算出
鏡像法は、電荷だけでなくインダクタンスを考える時にも適用できます。対地側に逆方向を向く鏡像電流-Iが流れていると仮定する。
アンペールの法則により、導体の間(0<z<h-a)で発生する磁束密度は
\begin{aligned}B(z)=\dfrac{\mu_{o}I}{2 \pi (h-z)}+\dfrac{\mu_{o}I}{2 \pi (h+z)}\end{aligned}
これより、導体1と平板の間に鎖交する磁束\(\phi\)は
\begin{aligned}\phi&=\int^{h-a}_{0}\dfrac{\mu_{o}I}{2 \pi} \left ( \dfrac{1}{h-z}+\dfrac{1}{h+z} \right ) dz \\ &=\dfrac{\mu_{o}I}{2 \pi} \left \lbrack -\log(h-z) + \log (h+z) \right \rbrack^{h-a}_{0} \\ &= \dfrac{\mu_{o}I}{2 \pi} \log \dfrac{2h-a}{a} \\ & \fallingdotseq \dfrac{\mu_{o}I}{2 \pi} \log \dfrac{2h}{a} \end{aligned}
以上より、求めるインダクタンスは、\(\phi=LI\)より
\begin{aligned}L=\dfrac{\mu_{o}}{2 \pi} \log \dfrac{2h}{a}\end{aligned}
(4)導体2にかかる電圧
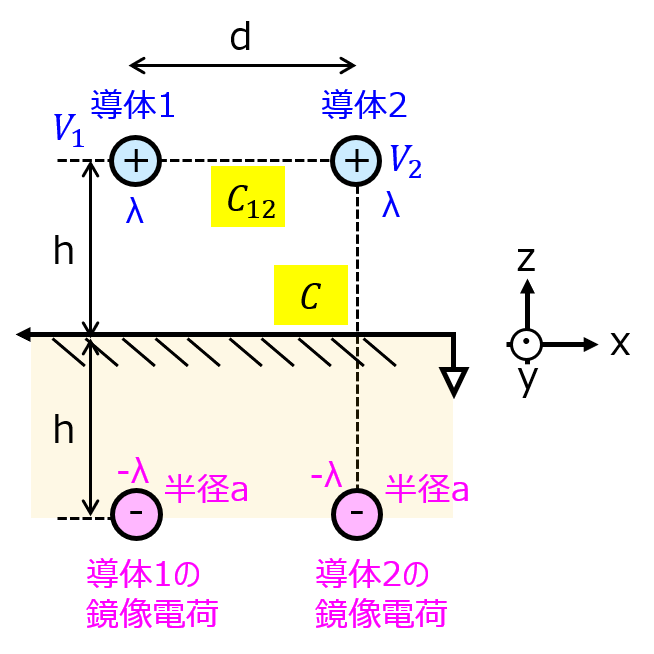
まず、導体1と導体2の間の静電容量\(C_{12}\)について考える。
(4)式の結果の2hをdに置き換えれば良いので
\begin{aligned}C_{12}=\dfrac{2 \pi \varepsilon_{o}}{\log\dfrac{d}{a}}\end{aligned}
上記の図のように、導体1-導体2-接地平板との直列回路を考える。
導体2にかかる電圧\(V_{2}\)は静電容量の逆比になるため、(4)式(5)式から
\begin{aligned}V_{2}&=\dfrac{C_{12}}{C+C_{12}}V_{1} \\ &= \dfrac{\dfrac{2 \pi \varepsilon_{o}}{\log\dfrac{d}{a}}}{\dfrac{2 \pi \varepsilon_{o}}{\log\dfrac{d}{a}}+\dfrac{2 \pi \varepsilon_{o}}{\log\dfrac{2h}{a}}}V_{1} \\ &=\dfrac{\log\dfrac{2h}{a}}{\log\dfrac{2h}{a}+\log\dfrac{d}{a}}V_{1}\end{aligned}
最後に
本問も、よく院試で出題されます。最後の問題だけやや難しいですが、基本事項の組み合わせで解くことができます。(1)(2)はマストで解けるようになりましょう。