下記の系のベクトルポテンシャルをそれぞれ求めよ。なお、いずれの系も真空中に置かれているとし、誘電率、透磁率はそれぞれ\(\varepsilon_{o},\mu_{o}\)とする。
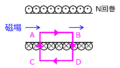
(1)長さ\(a\)の導線1,2が距離\(d\)離れて正対している。導体1の-a/2~a/2の範囲を流れる電流\(I\)により、導体2の任意の点(b,d)におけるベクトルポテンシャルを求めよ。なお、必要に応じて下記の式を用いて良い。
\begin{aligned}\int\dfrac{dx}{x^{2}+\sqrt{x^{2}+b^{2}}}=\log\left(x+\sqrt{x^{2}+b^{2}}\right)\end{aligned}
(2)xy平面に存在する磁気モーメント\(m\)からなる円環コイルがyz平面の任意の点(0,y,z)で発生するベクトルポテンシャル。
(3)xy平面に存在する無限に長い導体板(厚さ1)がx軸+方向に電流密度\(J\)で電流が流れている。z>0を満たす点P(x,y,z)で発生するベクトルポテンシャル。
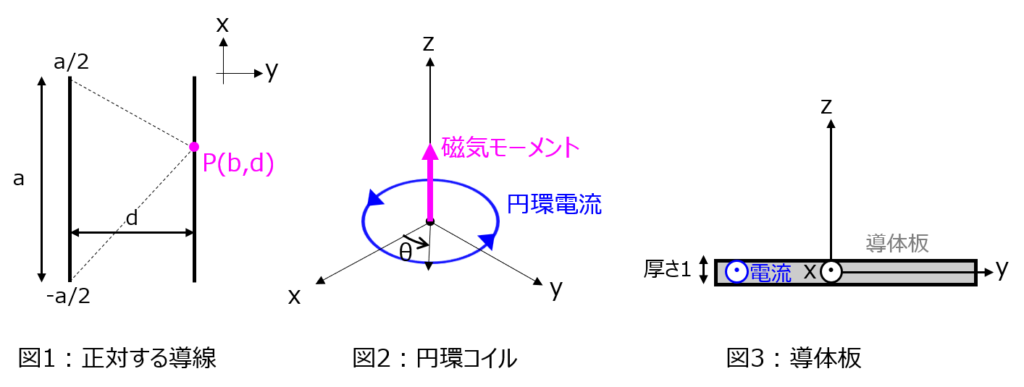
ベクトルポテンシャルとは
磁場(磁束密度)\(H,B\)に対するポテンシャル関数\(A\)を言います。
\begin{aligned}\boldsymbol{B}=rot(\boldsymbol{A})\end{aligned}
で表されます。よく、電場\(E\)に対するポテンシャルを電位\(V\)として表現していますが、これの磁場バージョンになります。
下記の式で表されます。
\begin{aligned}\boldsymbol{A}=\dfrac{\mu_{o}}{4 \pi } \int_{c} \dfrac{I d\boldsymbol{r}}{\boldsymbol{r}-\boldsymbol{r’}}\end{aligned}
電場は、電荷が存在するだけで発生しますが、磁場は電荷が移動(電流になる)ことで発生します。そのため、ベクトルポテンシャルは電流を変数に持っています。
また、円環電流など、磁気モーメント\(m\)を定義できる条件下においては、外積を用いて下記で表されます。
\begin{aligned}\boldsymbol{A}=\dfrac{\mu_{o}}{4 \pi } \int_{c} \dfrac{\boldsymbol{m} × d\boldsymbol{r}}{\boldsymbol{r}-\boldsymbol{r’}}\end{aligned}
ベクトルポテンシャルによる電場-磁場の結びつき
- 磁場:ベクトルポテンシャルの回転により発生
- 電場:ベクトルポテンシャルの時間変化により発生
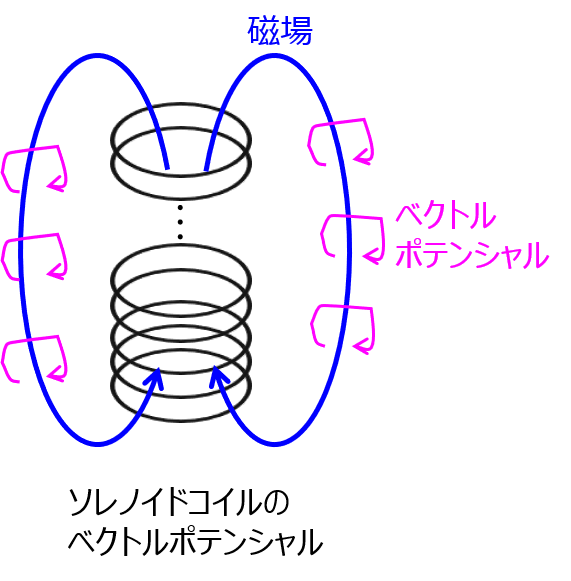
前節の説明により、ベクトルポテンシャルは磁場を発生させるポテンシャル関数です。右ねじの法則により、ベクトルポテンシャルの回転を取ると磁場になります。
\begin{aligned}\boldsymbol{B}=rot\boldsymbol{A}\end{aligned}
また、磁場と電場には、電磁誘導の法則により、下記の関係があります。
\begin{aligned}rot\boldsymbol{E}=-\dfrac{\partial \boldsymbol{B}}{\partial t}\end{aligned}
上記の式を適用すると、電場とベクトルポテンシャルでも関係式が導かれます。
\begin{aligned}rot\boldsymbol{E}=-\dfrac{\partial}{\partial t}rot\boldsymbol{A} \end{aligned}
\begin{aligned}\boldsymbol{E}=-\dfrac{\partial \boldsymbol{A}}{\partial t}\end{aligned}
よって、電場はベクトルポテンシャルの時間変化で発生することが分かりました。
ベクトルポテンシャルの意味
工学部の院試ではあまり出ませんが、教養として知っておくと一生モノです。
電場、磁場は、ローレンツ力\((F=qvB+qE)\)に関わるため、荷電粒子の力に対して影響を及ぼします。
一方で、ベクトルポテンシャルは、荷電粒子の運動量に対して影響を及ぼします。
これは、古典力学のクーロンの法則\(F=qE\)を例にして考えると分かりやすいです。
(7)式により、\(F=-q\dfrac{\partial A}{\partial t}\)に分解できるわけですから、これは古典力学における運動量\(P=\dfrac{\partial P}{\partial t}\)に対応します。(運動量\(m\dfrac{dx}{dt}\)のうち、\(m\)は\(q\)、\(\dfrac{dx}{dt}\)は\(\dfrac{\partial P}{\partial t}\)に対応。)
よって、磁場中に荷電粒子が入った場合は、運動量を得ることが分かりました。
解答例
(1)導体から発生するベクトルポテンシャル
与えられた座標系により、電流はx方向にのみ流れる。y,z方向のベクトルポテンシャルは0になる。
\begin{aligned}A_{y}=A_{z}=0\end{aligned}
x方向のベクトルポテンシャル\(A_{x}\)は、
\begin{aligned}A_{x}&=\dfrac{\mu_{o}I}{4 \pi }\int^{a/2}_{-a/2}\dfrac{1}{\sqrt{(x+b)^{2}+d^{2}}}dx \\ &=\dfrac{\mu_{o}I}{4 \pi }\left \lbrack \log(x+b+\sqrt{(x+b)^{2}+d^{2}} \right \rbrack ^{a/2}_{-a/2} \\ &= \dfrac{\mu_{o}I}{4 \pi }\log \left ( \dfrac{\frac{a}{2}+b+\sqrt{(\frac{a}{2}+b)^{2}+d^{2}}}{-\frac{a}{2}+b+\sqrt{(-\frac{a}{2}+b)^{2}+d^{2}}}\right) \end{aligned}
(2)円環コイルから発生するベクトルポテンシャル
円環電流は\(\theta\)方向、点Pまでの経路は\(r\)方向により、外積を取ると磁気モーメント\(m\)はz方向のみ存在する。
\begin{aligned}\boldsymbol{m}×\boldsymbol{r}&=\begin{vmatrix}
\widehat{x} & \widehat{y} & \widehat{z} \\
0 & 0 & m \\ 0 & y & z\phi \end{vmatrix} \\ &=(-my,0,0)\end{aligned}
これと(3)式を組み合わせる。\(r=\sqrt{y^{2}+z^{2}}\)より
\begin{cases}A_{x}=-\dfrac{\mu_{o}my}{4 \pi (y^{2}+z^{2})^{3/2}} \\ A_{y}=A_{z}=0\end{cases}
(3)無限導体板から発生するベクトルポテンシャル
まず、磁束密度\(B\)を求めて、\(\boldsymbol{B}=rot \boldsymbol{A}\)を用いることで求めます。
右ねじの法則により、磁場は電流の回転で発生する。
よって、z>0の領域では+y方向、z<0の領域では-y方向の磁場が発生する。
長辺e、短辺fの矩形の閉曲面を導体をまたぐ領域において配置すると、アンペールの法則により
\begin{aligned}Jf=2\mu_{o}Bf \\ B=\dfrac{\mu_{o}J}{2}\end{aligned}
ベクトルポテンシャルの向きは、電流ベクトルの向きと一致するため
\begin{aligned}A_{y}=A_{z}=0\end{aligned}
\begin{aligned}rot\boldsymbol{A}&=\begin{vmatrix}
\widehat{x} & \widehat{y} & \widehat{z} \\
\dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ A_{x} & 0 & 0 \end{vmatrix} \\ &=(0,\dfrac{\partial A_{x}}{\partial z},-\dfrac{\partial A_{x}}{\partial y})\end{aligned}
z方向の磁場は発生しないので、\(-\dfrac{\partial A_{x}}{\partial y}=0\)
よって、y成分の方程式を解けばよく
\begin{aligned}\dfrac{\partial A_{x}}{\partial z}=\dfrac{\mu_{o}J}{2} \\ A_{x}=\dfrac{\mu_{o}Jz}{2}\end{aligned}
最後に
ベクトルポテンシャルに関する問題は、何年かに一度のペースで出題されることがあります。(大学によりますが)
電流ベクトルと同じ成分であることに注目して解くことが多いです。最低限これだけは覚えておきましょう。