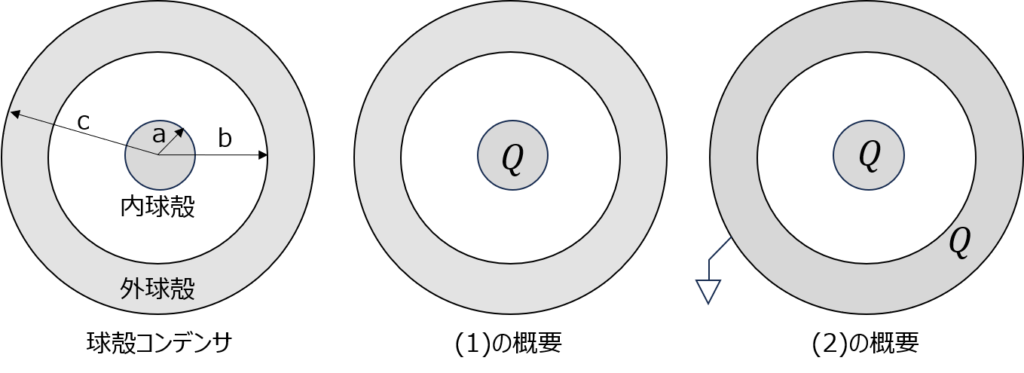
下図のように、内径\(a\)、外球殻の径が短い方から\(b,c\)の球殻コンデンサがある。下記(1)~(5)の操作をそれぞれ行ったときの電荷分布、電場分布を求めよ。
(1)内径に電荷Qを与えたとき
(2)内径に電荷Q、外球殻に電荷Qを与えたとき
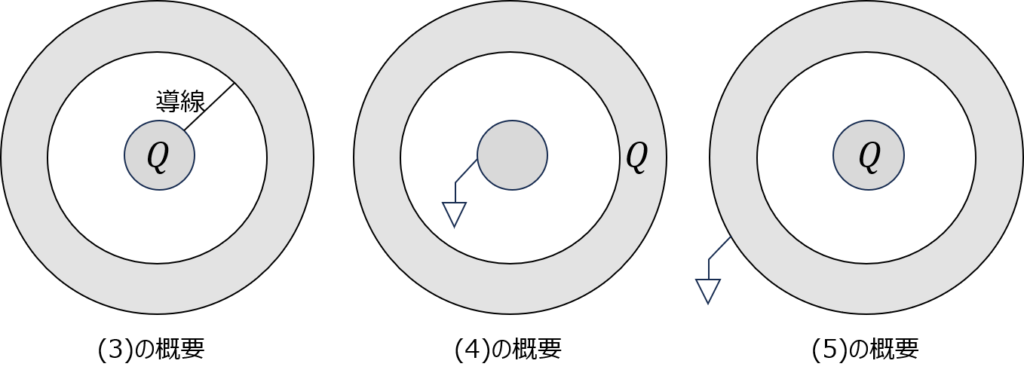
(3)内径に電荷Qを与えて、外球殻と細い導線で繋げたとき
(4)内径を接地し、外球殻に電荷Qを与えたとき
(5)内径に電荷Qを与えて、外球殻を接地したとき
はじめに
コンデンサに電荷を与え、その時の電場分布を計算する問題は院試頻出です。必ず対策する分野です。
電磁気学の勉強をやり込んでいると、接地、極板間を導線で繋ぐなどの各種操作を行ったときに発生する現象を何となく解けてしまっていることが多いです。
ですが、少し深い問題を問われたときに困るかもしれません。
そこで、本記事ではコンデンサに様々な操作を行った時に発生する事象をそれぞれ言語化し、原則に基づいた解答をしていきたいと思います。
解法の原則
どの状況でも適用する条件
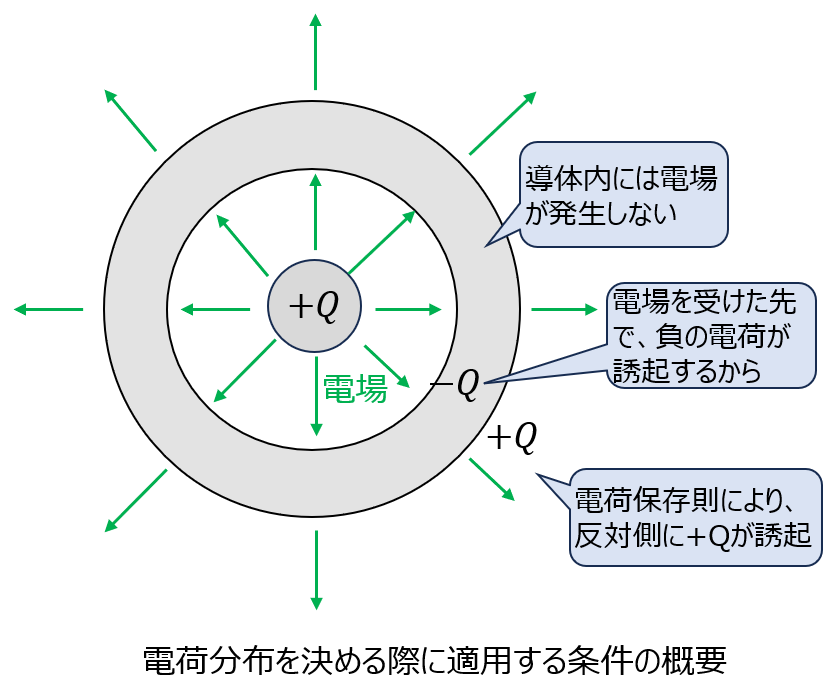
- 導体内部の電位差は0。
- 導体内部に電場は発生しない。
- 導体の電荷量は、初期に与えた電荷量から変化しない。(電荷保存則)
※他の導体との接続および接地した場合を除く - 上記3条件を満たすように電荷は分布する。
凄く基本的なことですが、系が複雑になるほど重要になってきます。下記、様々な状況を考えますが、試しに導体内部をガウスの法則で閉曲面で取ってみて、総電荷量が0(=電場0)になるかの確認は適宜行った方が良いと思います。
また、3.についても忘れないようにしましょう。問(1)が顕著ですが、内球に電荷を与えたことにより、外側球殻の内径側\(b\)に-Qが分布しますが、初期に設定した電荷は0であるため、最外球殻\(c\)に+Qが分布することにより、外側球殻全体で見た電荷保存則が成立します。
電荷を与えた際に発生する現象
- 設定した電荷から電場が発生し、電場を受ける先の導体で負の電荷が誘起する。
普段、何の気無しに極板間の電荷を+Q,-Qでセットで設定している方も少なくないのではないでしょうか。実際、それだけである程度のレベルの問題は解けてしまいます。
実際は、近接作用の立場から、電場が発生するから影響先の導体で負の電荷(-Q)が誘起する順序で電荷を設定していきます。そうでないと、複雑な系において電荷分布を設定する手順が分からず混乱してしまいます。
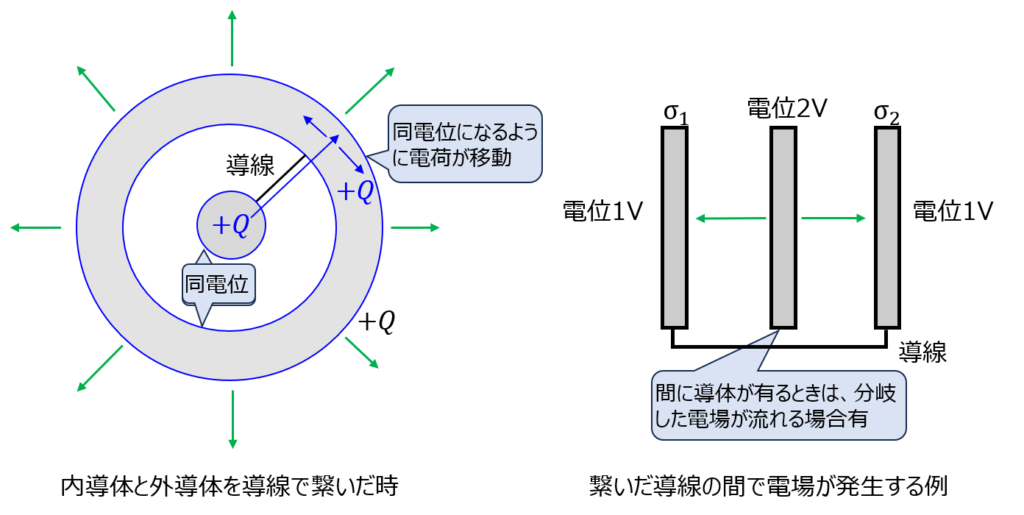
導体同士を導線で繋いだ時に発生する現象
- 導線で繋いだ導体同士は等電位になる。
- 等電位になるように接続した導体間で電荷の移動が可能になる。
厳密には、導線自体に電気抵抗が存在しており、電圧降下が発生しますが、電磁気学で本問を問われる際は無視することが多いです。ですので、等電位とみなせます。
等電位の要因があり、これを満たすために電荷が移動する因果関係になります。是非、逆にならないように気を付けましょう。
なお、等電位と言うからには接続した導体間で電場が発生しないと考えたくなります。しかし、系によっては当てはまらないことがあります。気を付けましょう。(例えば、上図の右側)
接地したときに発生する現象
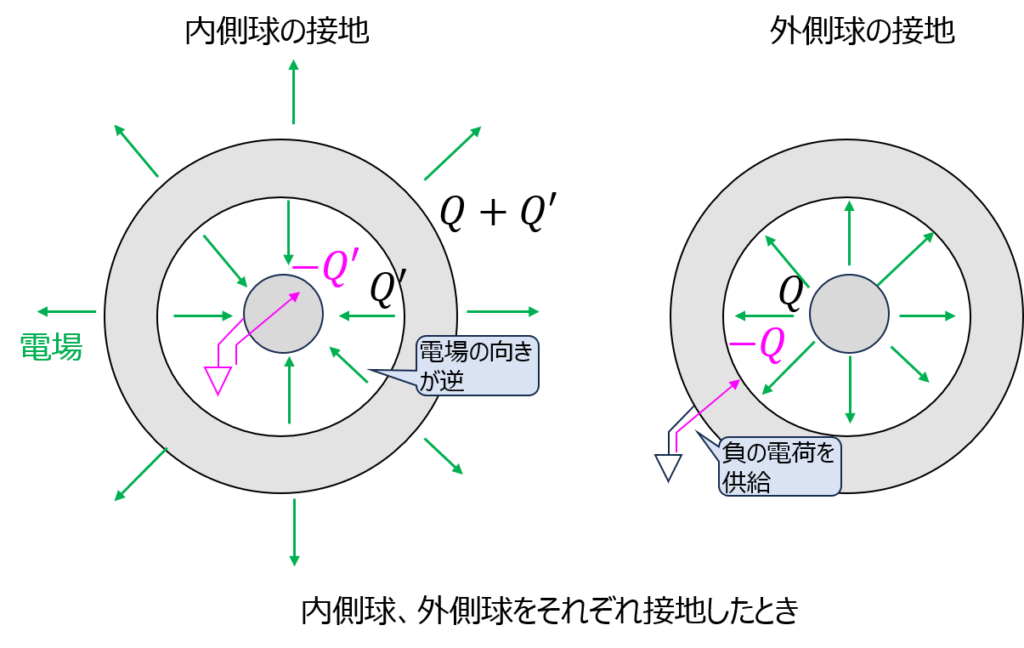
- 接地した導体の電位が0になる。
- 電位が0になるよう、アース(地面)から電荷が供給or吸収する。
もしかすると、本ケースが一番取っつきやすいと考える方も居るかもしれません。(筆者はそうです。)
よくあるケースとして、2つある極板の内一方に電荷を与え、もう一方は接地する場合です。接地側の導体においては、アースから自由に電荷の出し入れができますので、電荷保存則は適用しません。
あくまでも、電荷を与えた側の導体から発生する電場により、接地側の電位が0になるためにはどのような電荷分布が適切か?の視点で考えていけば良いです。
解答例
(1)内径に電荷Qを与えたとき
電荷分布
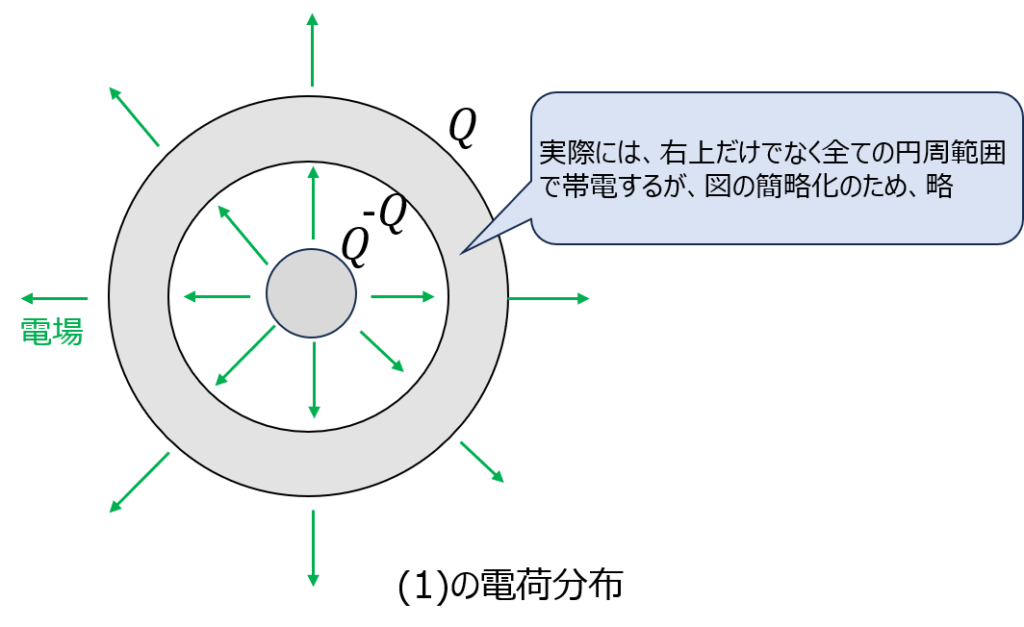
内径から発生する電場により、外球殻の内径側に電荷-Qが誘起する。電荷保存則より初期電荷は0なので、外球殻の外径側に電荷+Qが帯電する。
よって、図に表すと下記のような電荷分布になる。
電場分布
ガウスの法則より、半径rの球を閉曲面として取る。
(i) r<aのとき、閉曲面内に電荷が無いため、電場\(E_{1}=0\)
(ii)a<r<bのとき、閉曲面内に+Qの電荷が存在。
\begin{aligned}E_{2}=\dfrac{Q}{4 \pi \varepsilon_{o} r^{2}}\end{aligned}
(iii)b<r<cのとき、閉曲面全体の電荷の総量は0なので、電場\(E_{3}=0\)
(iv)c<rのとき、閉曲面内に+Qの電荷が存在。
\begin{aligned}E_{4}=\dfrac{Q}{4 \pi \varepsilon_{o} r^{2}}\end{aligned}
(2)内径に電荷Q、外球殻に電荷Qを与えたとき
一見すると、導体球同士が反発し合うのか?と心配になりますが、これも近接作用の概念で順を追って電荷の設定ができます。電荷保存則で考える外側球殻側の初期電荷が+Qなだけで、考え方は(1)と変わりません。
電荷分布
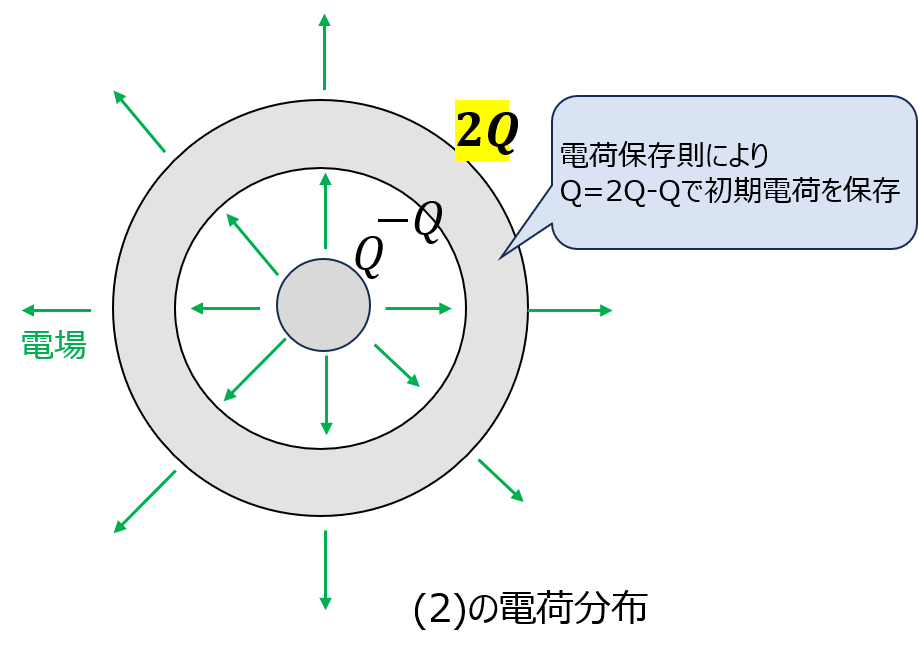
内径から発生する電場により、外球殻の内径側に電荷-Qが誘起する。電荷保存則より初期電荷は+Qなので、外球殻の外径側に電荷+2Qが帯電する。
よって、図に表すと下記のような電荷分布になる。
電場分布
(1)の結果を利用すると、(iv)だけ電荷量が+2Qになるので、ここだけ結果が変わる。
\begin{aligned}E_{4}=\dfrac{Q}{2 \pi \varepsilon_{o} r^{2}}\end{aligned}
※(i)~(iii)は(1)と同じ。
(3)内径に電荷Qを与えて、外球殻と細い導線で繋げたとき
電荷分布
内球と外側球殻の電位は等しくなるように電荷は分布する。接続した導体の間に他の導体は存在しない。よって、内球または外側球殻の内径に電荷を設定すると電場が発生し、電位差が発生するため、個の分布は不適。
外側球殻の外径側にしか電荷+Qは存在することができず、前節(導体同士を導線で繋いだときに発生する現象)と同じ電荷分布になる。
電場分布
(1)~(2)と同じく、半径rの球を閉曲面として取る。
(i)r<c のとき、電荷は存在しない。\(E_{1}=0\)
(ii)c<rのとき、電荷+Qが存在するため
\begin{aligned}E_{4}=\dfrac{Q}{4 \pi \varepsilon_{o} r^{2}}\end{aligned}
(4)内径を接地し、外球殻に電荷Qを与えたとき
冒頭で提示した問題の中で最難だと思います。内球の電位が0であることは絶対条件ですので、ある正の電位をもった外側球殻から内球に向かって電場が放射している。と考えます。
- アースから内球に供給する電荷を-Q'(未知数)とし、電荷分布を仮設定
- 仮設定した電荷分布から電場分布を求め、電位を算出する。
- 接地の条件より、内球の電位は0の条件を用いて未知数Q’を求める。
解答内容
未知数-Q’を内径に設定したことから、外球殻の内側に+Q’、最外殻にQ-Q’の電荷が分布します。
前節(導体を接地したときに発生する現象)の図左側をご覧ください。
この電荷分布において、電場を求めます。
(i)r<aのとき、\(E_{1}=0\)
(ii)a<r<bのとき
\begin{aligned}E_{2}=\dfrac{Q’}{4 \pi \varepsilon_{o} r^{2}}\end{aligned}
(iii)b<r<cのとき、\(E_{3}=0\)
(iv)r<cのとき
\begin{aligned}E_{4}=\dfrac{Q-Q’}{4 \pi \varepsilon_{o} r^{2}}\end{aligned}
以上を用いて、内径の電位Vは
\begin{aligned}V=\dfrac{1}{4 \pi \varepsilon_{o}}\left(\dfrac{Q-Q’}{c}-\dfrac{Q’}{a}+\dfrac{Q’}{b} \right)\end{aligned}
接地しているので、上式はV=0になる。これを解いて
\begin{aligned}Q’=\dfrac{ab}{bc+ab-ac}Q\end{aligned}
を得る。最初に設定した未知数Q’にこれを代入することで、電荷分布が求められた。
電場分布についても、(i)~(iv)の結果に本結果を代入すれば良い。
(5)内径に電荷Qを与えて、外球殻を接地したとき
実は、(4)よりもこっちの方が簡単だったりします。
電荷分布
内球+Qから発生する電場により、外側球殻の内径側に-Qの電荷が帯電する。
外側球殻の電荷は、アースから自由に出入りできるので、(1)のように外側球殻の外側に-Qの電荷は帯電しない。
前節(導体を接地したときに発生する現象)右側の図になります。
電場分布
r<cについては、(1)の結果と同じです。
r>cについては、外側球殻の外側に電荷が無いので変わらず\(E_{4}=0\)になります。
最後に
今回は球殻コンデンサを題材にしましたが、円筒型、平板コンデンサについても基本となる考え方は同じです。
是非、解法の原則の内容を理解し、解答の幅を広げましょう。