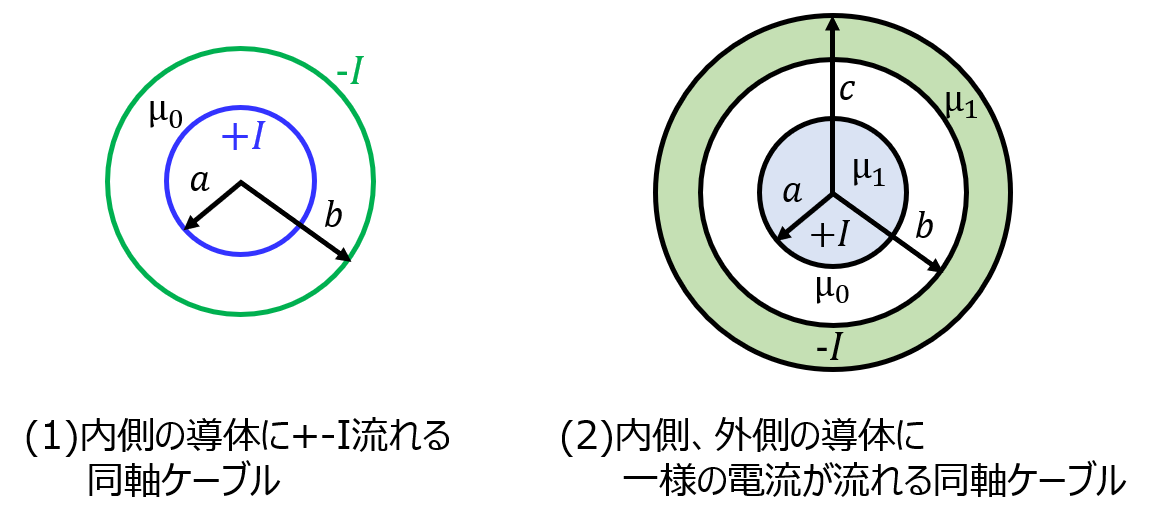
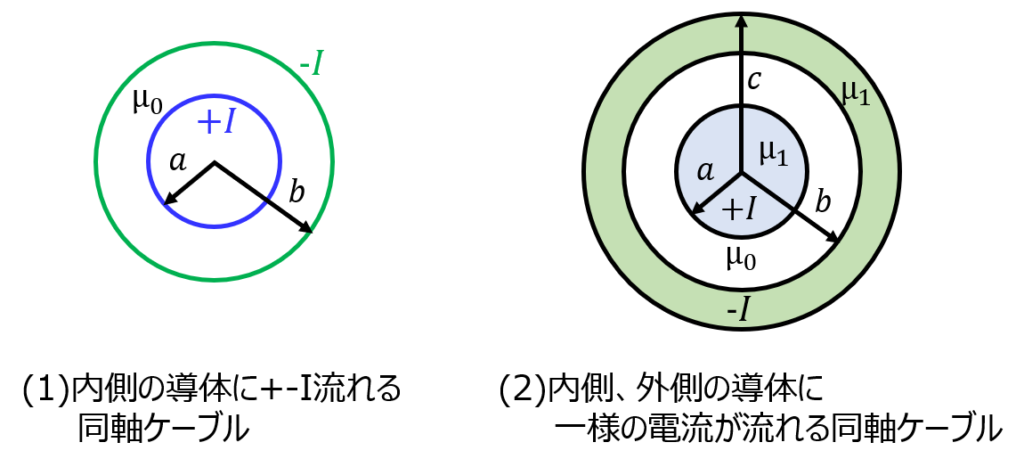
下記の図(a)(b)内側導体、外側導体で構成される同軸ケーブルそれぞれの自己インダクタンスを求めよ。ただし、長さは無限長とする。真空中の透磁率は\(\mu_{0}\)、導体中の透磁率は\(\mu_{1}\)とする。
(1)内側の導体に+I、外側の導体に-I流れる同軸ケーブル
(2)内側の導体に+I、外側の導体に-I流れる同軸ケーブル。ただし、各導体中の電流は一様に流れているとする。
はじめに
本問、意外と(2)が難しかったりします。
(1)は典型問題で、市販の問題集でもよく見かける問題です。アンペールの法則を適用し、磁束密度を内側、外側導体の間の空間(半径\(a<r<b\)の区間)で積分すれば良いです。
しかし、(2)はどうでしょうか。
(1)とは異なり電流が一様に流れていますので、半径rによって電流が増減する区間が発生します。ここのインダクタンスの計算方法を原理原則から理解していないと、正答することはできません。
解答例
(1)同軸ケーブルのインダクタンス
アンペールの法則を半径\(r\)の円筒で取る。
\begin{eqnarray}\int _{c}B\cdot ds=\mu _{0}\int _{s}ids\end{eqnarray}
\begin{eqnarray}B\left( r\right) \cdot 2\pi r=\mu_{0} I\left( r\right)\end{eqnarray}
(i)\(0<r<a\)のとき
電流が流れていないので\(I=0\)。よって、\(B_{a}=0\)
(ii)\(a<r<b\)のとき、(2)式より
\begin{eqnarray}B_{b}=\dfrac{\mu_{0} I}{2\pi r}\end{eqnarray}
(iii)\(b<r\)のとき、閉路内の電流の総量は0
よって、(i)と同じく\(B_{c}=0\)
以上より、(ii)の範囲で単位面積当たりの磁束\(\Phi\)を計算する。
\begin{eqnarray}\Phi =\int ^{b}_{a}\dfrac{\mu _{0}I}{2\pi r}dr \\ = \dfrac{\mu_{o} I}{2\pi }\log \dfrac{b}{a}\end{eqnarray}
\(\Phi=LI\)より、求めるインダクタンスは
\begin{eqnarray}L =\int ^{b}_{a}\dfrac{\mu _{0}I}{2\pi r}dr \\ = \dfrac{\mu_{0}}{2\pi }\log \dfrac{b}{a}\end{eqnarray}
(2)電流が一様に流れる同軸ケーブルのインダクタンス
全体方針
内側導体の自己インダクタンスを\(L_{1}\)、外側導体の自己インダクタンスを\(L_{2}\)、二つの導体の相互インダクタンスを\(M\)とする。
導体全体のインダクタンス\(L\)は、下記のように求められます。
\begin{eqnarray}L=L_{1}+L_{2}+2M\end{eqnarray}
※\(M\)は、内側導体から見た外側導体の相互インダクタンス\(M_{12}\)と
その逆、外側導体からみた内側導体の相互インダクタンス\(M_{21}\)を2つ足しているので\(2M\)となっています。\(M_{12}=M_{21}\)です。
内側導体\(0<r<a\)のインダクタンス\(L_{1}\)の求め方
巻き数の概念が非常に重要になります。
導体内では、物理的に銅線が巻かれているわけではありません。しかし、一様に電流が流れているため、電流の強弱は発生しています。
これを巻き数として表現し、自己インダクタンスの計算に加える必要があります。
まず、電流密度\(J_{1}\)を考える。電流値を面積で割れば良いので
\begin{eqnarray}J_{1}=\dfrac{I}{\pi a^{2}}\end{eqnarray}
アンペールの法則から
\begin{aligned}B_{1} \cdot 2 \pi r&=\dfrac{\mu_{0} I}{\pi a^2} \cdot \pi r^{2} \\ B_{1}&=\dfrac{\mu_{0} I}{2 \pi a^2}r\end{aligned}
これを区間0<r<aで積分し、鎖交磁束を求める。
微小区間の磁束\(d\phi\)は、下記式で表すことができる。
\begin{eqnarray}d\phi=\dfrac{\mu_{0} I}{2 \pi a^2}rdr\end{eqnarray}
鎖交磁束と磁束の関係は、巻き数\(N\)を用いて下記式で与えられる。
\begin{eqnarray}d\Phi=Nd\phi\end{eqnarray}
\begin{eqnarray}N=\dfrac{r^{2}}{a^{2}}\end{eqnarray}
(14)式が重要です。電流Iがフルに流れている区間を巻き数1とし、それを面積によって比を取るということですね。
以上より、
\begin{eqnarray}d\Phi=\dfrac{r^{2}}{a^{2}}\cdot \dfrac{\mu_{0}I}{2 \pi a^2}rdr\end{eqnarray}
区間\(0<r<a\)で積分して
\begin{aligned}\Phi&=\dfrac{\mu_{1}I}{2 \pi a^{4}}\int _{0}^{a}r^{3}dr \\ &= \dfrac{\mu_{1}I}{2 \pi a^{4}} \cdot \dfrac{a^{4}}{4} \\ &= \dfrac{\mu_{1} I}{8 \pi} \end{aligned}
\(\Phi=L_{1}I\)より
\begin{eqnarray}L_{1}=\dfrac{\mu_{1}}{8\pi}\end{eqnarray}
内側導体-外側導体の間の相互インダクタンス\(2M\)
(1)の結果(7)式を利用して
\begin{eqnarray}2M=\dfrac{\mu_{o}}{2\pi }\log \dfrac{b}{a}\end{eqnarray}
外側導体\(b<r<c\)の自己インダクタンス\(L_{2}\)
内側導体の自己インダクタンスの求め方と同様にして求めていく。
電流密度\(J_{2}\)は
\begin{eqnarray}J_{2}=\dfrac{I}{\pi c^{2}-b^{2}}\end{eqnarray}
\begin{aligned}2 \pi r B_{3}&=\mu_{1} \left( I-\dfrac{\pi \left( r^{2}-b^{2}\right) }{\pi \left( c^{2}-b^{2}\right)I }\right) \\ &=\dfrac{\mu_{1} I}{2\pi r}\dfrac{r^{2}-b^{2}}{c^{2}-b^{2}}\end{aligned}
\begin{eqnarray}N=\dfrac{\pi (c^{2}-r^{2})}{\pi (c^{2}-b^{2})}=\dfrac{c^{2}-r^{2}}{c^{2}-b^{2}}\end{eqnarray}
\begin{aligned}\Phi &=\dfrac{\mu _{1}I}{2\pi \left( c^{2}-b^{2}\right) ^{2}}\int _{b}^{c}\dfrac{\left( c^{2}-r^{2}\right) ^{2}}{r}dr\\ &=\dfrac{\mu _{1}I}{2\pi \left( c^{2}-b^{2}\right) ^{2}}\int _{b}^{c}\dfrac{c^{4}-2c^{2}r^{2}+r^{4}}{t}dr \\ &=\dfrac{\mu _{1}I}{2\pi \left( c^{2}-b^{2}\right) ^{2}} \left[ c^{4}\log r-cr^{2}+\dfrac{r^{4}}{4}\right] _{b}^{c} \\ &=\dfrac{\mu _{1}I}{2\pi \left( c^{2}-b^{2}\right) ^{2}} ( c ^{4}\log \dfrac{c}{b}-c^{2}\left( c^{2}-b^{2}\right) +\dfrac{c^{4}-b^{4}}{4}) \end{aligned}
\(\Phi=L_{2}I\)より
\begin{aligned}L_{2}=\dfrac{\mu _{1}}{2\pi \left( c^{2}-b^{2}\right) ^{2}}\left( c ^{4}\log \dfrac{c}{b}-c^{2}\left( c^{2}-b^{2}\right) +\dfrac{c^{4}-b^{4}}{4}\right) \end{aligned}
全体のインダクタンス
式(19)(20)(26)を足し合わせて
\begin{aligned}L&=L_{1}+L_{2}+2M \\ &=\dfrac{\mu_{1}}{8\pi}+\dfrac{\mu_{0}}{2\pi }\log \dfrac{b}{a} + \dfrac{\mu _{1}}{2\pi \left( c^{2}-b^{2}\right) ^{2}}\left( c ^{4}\log \dfrac{c}{b}-c^{2}\left( c^{2}-b^{2}\right) +\dfrac{c^{4}-b^{4}}{4}\right)\end{aligned}
最後に
(2)は、計算が面倒ですが、やり方さえ押さえれば決して難しい問題ではありません。
一度流れをマスターすることをオススメします。