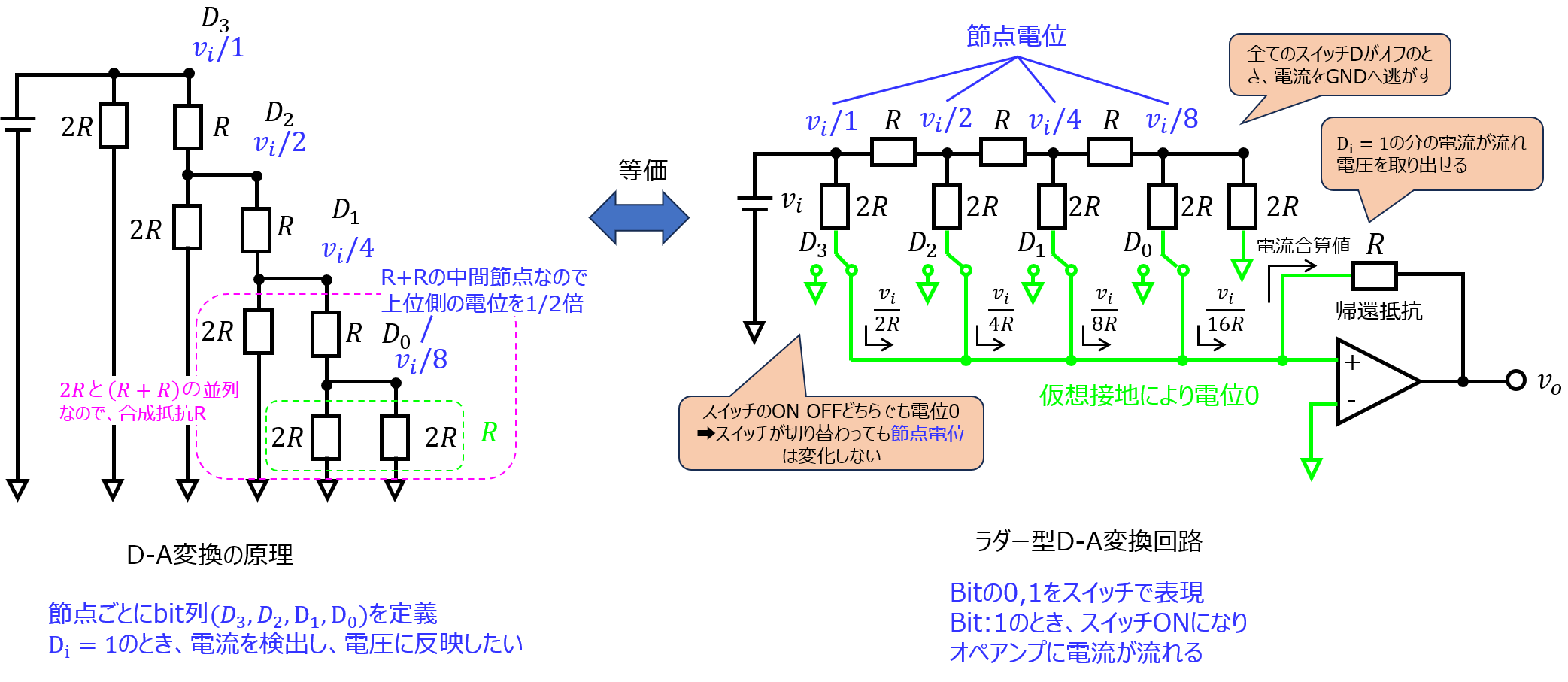
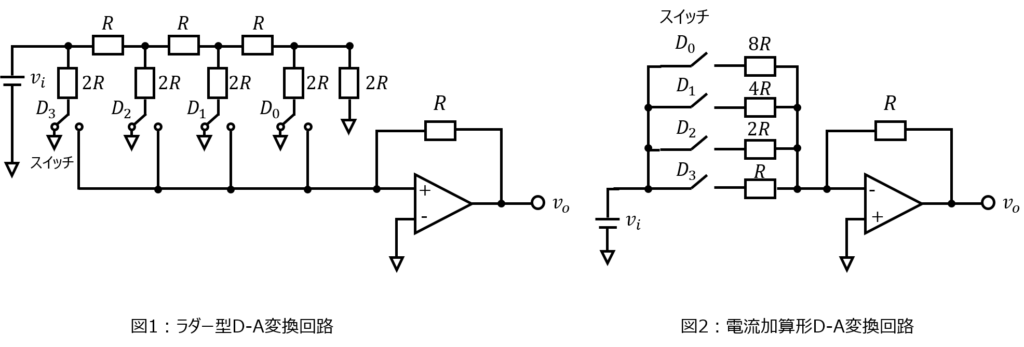
(1)図1に、ラダー型D-A変換回路を示す。動作原理を述べるとともに、出力電圧\(v_{o}\)の最大、最小値を絶対値で求めよ。また、その時の各スイッチ\(D_{i} (i=0,1,2,3)\)の状態も示せ。
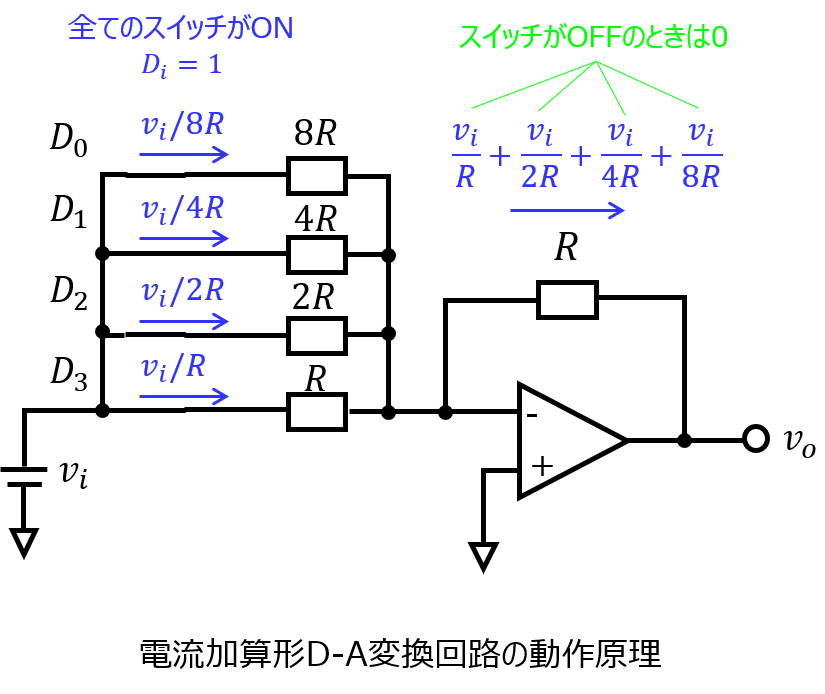
(2)図2に、電流加算型D-A変換回路を示す。動作原理を述べるとともに、出力電圧\(v_{o}\)の最大、最小値を絶対値で求めよ。また、その時の各スイッチ\(D_{i} (i=0,1,2,3)\)の状態も示せ。
(3)それぞれの回路は、bit数が多くなると発生する欠点が存在する。その内容をそれぞれ述べよ。
それぞれのD-A変換器の動作原理
回路構成に違いはあれど、基本的な考え方は下記です。
ディジタル信号のあるbitが1のとき、対応する節点スイッチがONになり、オペアンプ側に電流が流れる。
(1)ラダー型D-A変換器の動作原理
少し回路構成が複雑ですが、原理から説明していきます。(下記図)
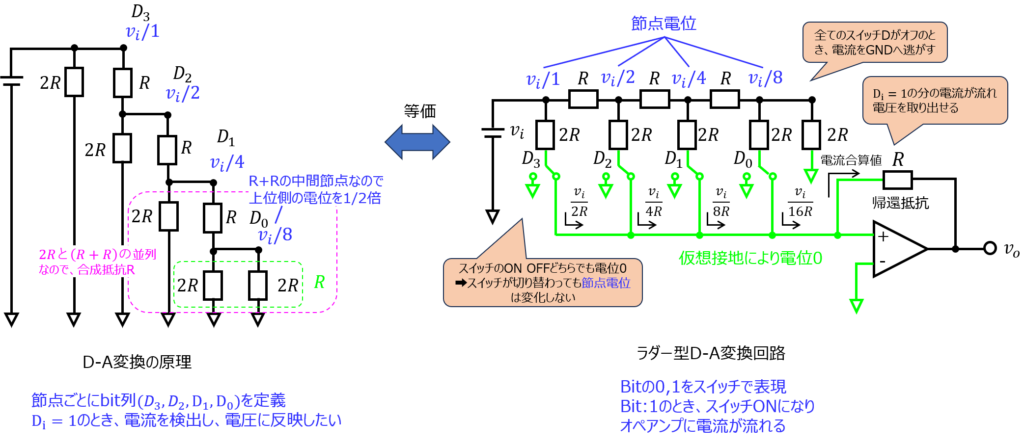
まず、抵抗値が2RとRに分かれているのには理由があります。2Rと2Rの並列回路が存在するとき、合成抵抗がRになるためです。
これを用いると、最下段の2R*2Rの並列抵抗をRに合成できます。(緑枠の領域)
上位側の抵抗Rとくっつけると、また2R*2Rの並列抵抗が出来上がります。(ピンク枠の領域)
これが再帰的に繰り返されますので、各接点は決まった電位差で落ちていくことが予想できます。
例えば、最下段の緑枠の合成抵抗はRとなりますが、すぐ上にある抵抗Rとの間に節点を入れると、上位側の電位を1/2倍したものになります。
これが他の節点にも言えますので、ラダー型で回路を組めば節点ごとに電圧が1/2倍されることが分かります。
例として、入力電圧1V、抵抗R=1Ωのときを考えます。
・\(D_{3}=1\)のとき、電流が0.5A発生し、帰還抵抗には0.5Vの電圧が立ちます。
・\(D_{2}=1\)のとき、電流が0.25A発生し、帰還抵抗には0.25Vの電圧が立ちます。
・\(D_{1}=1\)のとき、電流が0.125A発生し、帰還抵抗には0.125Vの電圧が立ちます。
・\(D_{0}=1\)のとき、電流が0.0625A発生し、帰還抵抗には0.0625Vの電圧が立ちます。
もし、帰還抵抗に立っている電圧が0.625Vのとき、0.5V+0.125Vと分解できますので、\(D_{3}=D_{1}=1\)であることが分かります。このように、1が立っているbit列をD-A変換することができます。
結局、一般形として、下記式で表せます。(節点ONのとき、\(D_{i}=1\))
\begin{aligned}v_{o}=(8D_{3}+4D_{2}+2D_{1}+D_{0})\dfrac{-v_{i}}{16}\end{aligned}
電圧最大値は、全ての節点がON
\(D_{0}=D_{1}=D_{2}=D_{3}=1\)になっているときで、\(|v_{o}|=(1/2+1/4+1/8+1/16)v_{i}\)
電圧最小値は、全ての節点がOFF
\(D_{0}=D_{1}=D_{2}=D_{3}=0\)になっているときで、\(|v_{o}|=0\)になります。
(2)電流加算型D-A変換回路
ラダー型D-A変換回路よりも簡単な構成で、こっちの方が分かりやすいかもしれません。
本回路は、抵抗を並列に取ります。ある節点がONのとき、ループが発生し、電流が流れます。
ラダー型と同じく、電流の大小=発生する電圧の大小により、1が立っているbitが分かります。ただ、電流の大小の実現方法が両者で異なります。
- ラダー型:抵抗を格子状に組むことにより、等比の電位差を実現。電位差により電流を調節する。
- 電流加算型:一次側の電圧は一定だが、抵抗により電流を調節する。
オームの法則V=IRとして考えると良いかもしれません。前者はVを調節するが、後者はRを調節し、結果同じ電流Iになるということですね。
結局、一般形として、下記式で表せます。(節点ONのとき、\(D_{i}=1\)
\begin{aligned}v_{o}=-\left(\dfrac{D_{3}}{R}+\dfrac{D_{2}}{2R}+\dfrac{D_{1}}{4R}+\dfrac{D_{0}}{8R}\right)Rv_{i}\end{aligned}
電圧最大値は、全ての節点がON
\(D_{0}=D_{1}=D_{2}=D_{3}=1\)になっているときで、\(|v_{o}|=\left(1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}\right)v_{i}\)
電圧最小値は、全ての節点がOFF
\(D_{0}=D_{1}=D_{2}=D_{3}=0\)になっているときで、\(|v_{o}|=0\)になります。
それぞれの変換器の欠点
(3)ラダー型D-A変換器
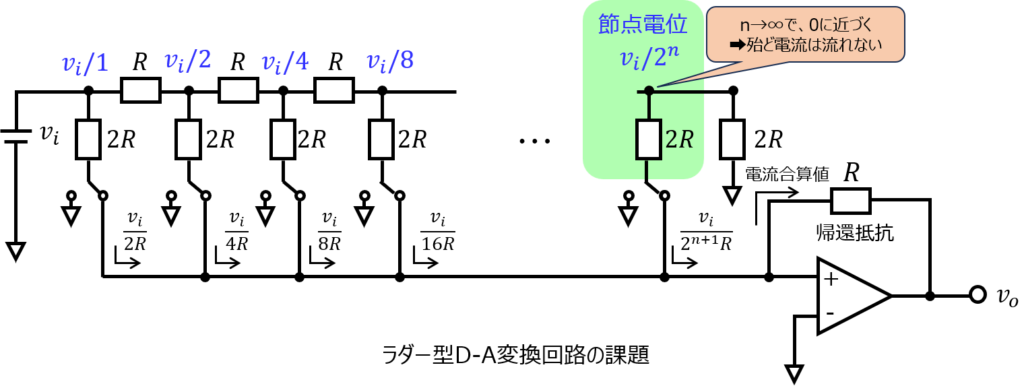
- 下側の段にある節点の電位が小さくなり、あまり電流が流れない。出力電圧値も立たなくなり、ノイズに埋もれる。(正しくD-A変換できない。)
- 入力電圧を大きくしなければならないが、それには限りがある。
段数が増えるごとに節点の電圧が1/2倍されることに注目します。その結果どうなるでしょうか。
細かくできる電圧にも限りがあります。入力電圧1Vのときは、1V➡0.5V➡0.25V➡…➡XXX mV とオーダーが落ちていきます。
その結果、段数が下側の節点から流れる電流は非常に小さいものとなり、電圧値として、ノイズに埋もれてしまう課題があります。
これを解決するために、供給電圧を上げることもできますが、やはり限りがあります。(そもそも、電子部品にかけられる電圧はたかが知れています。)
(3)電流加算型D-A変換回路
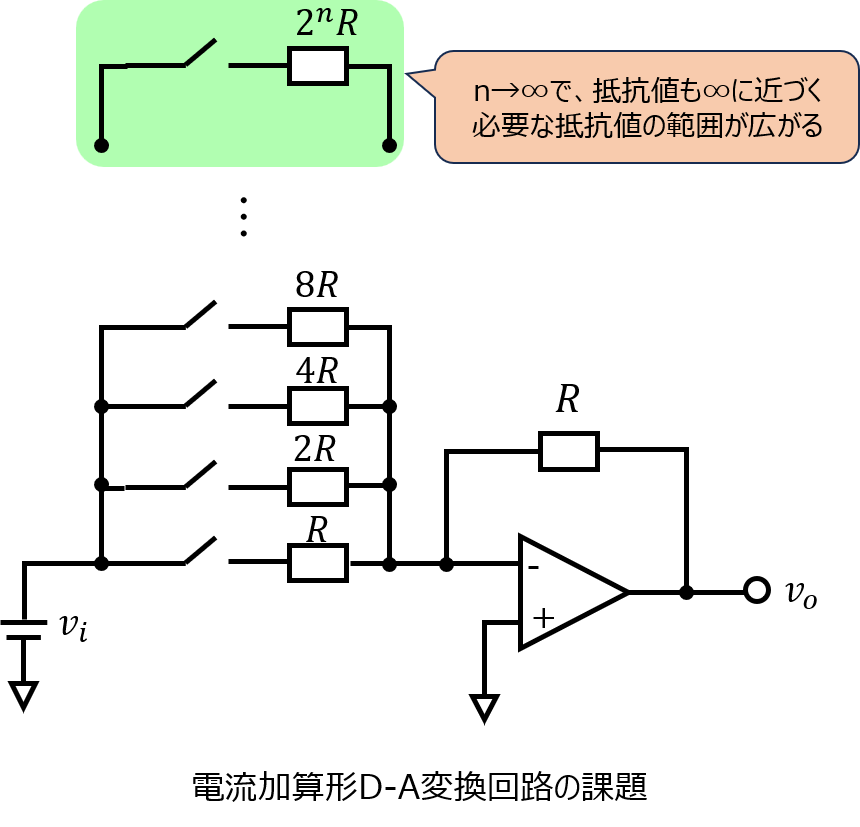
- 大きな抵抗を準備する必要がある
- 大きな抵抗を流れる電流値は小さくなるため、出力電圧が立ちづらくなる。ノイズに埋もれる。(正しくD-A変換できない。)
二つ目の欠点はラダー型回路と同じです。一つ目の欠点が新たに加わります。
前章で述べたように、電流加算型D-A変換回路は、抵抗値の大小により、電流の大小を調節します。
そうなると、今度は接続する抵抗の問題が発生します。
大きくできる抵抗にも限りがあるので、ハード的な制約から増やせる段数にも限度があります。