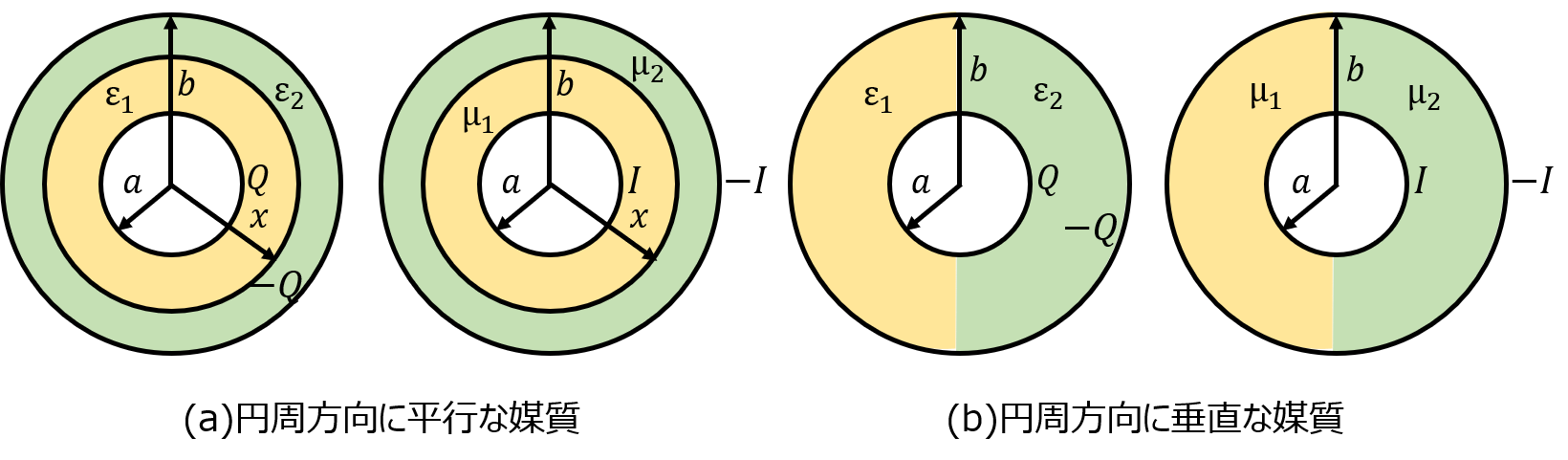
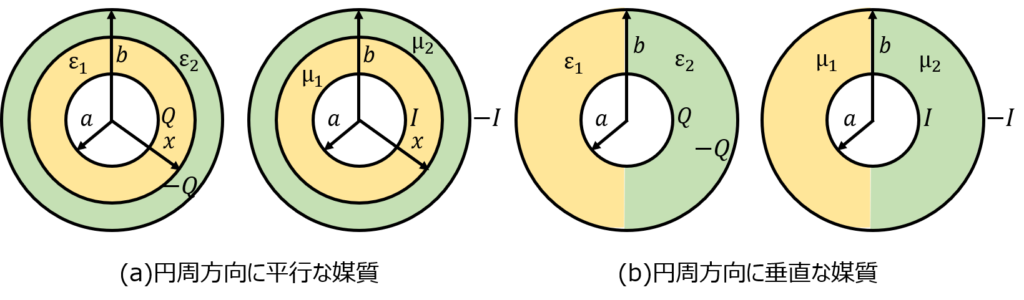
下記の図のように、内側の半径\(a\)、外側の半径\(b\)の同軸ケーブルが存在する。
円周の間に異なる媒質を次のように挿入した。
(a)円周方向に平行な媒質\(\varepsilon_{1},\mu_{1},\varepsilon_{2},\mu_{2}\)
(b)円周方向に垂直な媒質\(\varepsilon_{1},\mu_{1},\varepsilon_{2},\mu_{2}\)
(a)(b)それぞれの\(a<r<b\)の範囲の電場\(E\)、磁場\(H\)を求めよ。
ただし、\(Q\)は円筒側面の単位面積あたりの電荷とする。
また、電流\(I\)は紙面に向かってくる方向を正とする。
はじめに
本問は、九大で良く出題されます。
一般的に、同軸ケーブルで発生する電場を求めるならばガウスの法則。磁場を求めるならばアンペールの法則を使用すると良いです。
しかし、本問のように媒質が2つ以上あると追加で必要な考え方があります。
本問で覚えてほしいこと
- 電場\(E\)と磁場\(H\)は、異なる媒質間の接線成分で連続。
- 電束密度\(D\)と磁束密度\(B\)は、異なる媒質間の垂直成分で連続。
- 円周方向に平行な媒質のとき、電束密度\(D\)と磁場\(H\)が連続であることを利用する。
- 円周方向に垂直な媒質のとき、電場\(E\)と磁束密度\(B\)が連続であることを利用する。
1.2.については、よく教科書で解説されています。他サイトでも多数の解説があるため、本記事では導出過程を省略します。
1.2.の事実を用い、問題を解いていきます。電場\(E\)は半径\(r\)方向、磁場\(H\)は円周\(\theta\)方向に発生します。このため、電場は(b)の媒質で連続になります。磁場は、(a)の媒質で連続になります。これが3.4.を表します。
解答例
(a)円周方向に平行な媒質
電場の算出
前章の解説により、電束密度\(D\)が\(\varepsilon _{1},\varepsilon _{2}\)の間で連続。
電束密度によるガウスの法則から\(a<r<b\)の範囲において
\begin{aligned}\int_{V} \boldsymbol{D}\cdot d\boldsymbol{s}=Q\\ \boldsymbol{D} \cdot 2\pi r=Q\widehat{\boldsymbol{r}} \\ \boldsymbol{D}=\dfrac{Q}{2\pi r}\widehat{\boldsymbol{r}} \\ D=\dfrac{Q}{2\pi r}\end{aligned}
あとは、媒質1 \(\varepsilon _{1}(a<r<x)\)と媒質2 \(\varepsilon _{2}(x<r<b)\)で電場に変換し
\begin{cases}E_{1}=\dfrac{D}{\varepsilon _{1}}=\dfrac{Q}{4\pi r\varepsilon _{1}}(a <r <x) \\ E_{2}=\dfrac{D}{\varepsilon _{2}}=\dfrac{Q}{4\pi r\varepsilon _{2}}\left( x<r <b\right) \end{cases}
磁場の算出
境界面において磁場\(H\)は連続なので
磁場によるアンペールの法則から、\(a<r<b\)の領域において
\begin{aligned}\int_{c} H\cdot ds=I \\ H \cdot 2\pi r=I\\ H=\dfrac{I}{2\pi r}\end{aligned}
なお、磁束密度\(B\)に直すと
\begin{cases}B_{1}=\mu_{1}H=\dfrac{\mu_{1}I}{2\pi r } (a<r<x)\\ B_{2}=\mu _{2}H=\dfrac{\mu_{2}I}{2\pi r} (x<r<b) \end{cases}
(b)円周方向に垂直な媒質の場合
電場の算出
媒質の境界面は\(r\)方向である。よって、電場もr方向を向くので連続になる。
媒質1に帯電する電荷を\(Q_{1}\)、媒質2に帯電する電荷密度を\(Q_{2}\)とすると
\begin{cases}Q_{1}+Q_{2}=Q \\ \dfrac{Q_{1}}{\varepsilon_{1} S}=\dfrac{Q_{2}}{\varepsilon _{2}S}\end{cases}
これを解いて
\begin{cases}Q_{1}=\dfrac{\varepsilon _{1}}{\varepsilon ,+\varepsilon _{2}}Q\\ Q_{2}=\dfrac{\varepsilon _{2}}{\varepsilon _{1}+\varepsilon _{2}}Q\end{cases}
よって、求める電場\(E\)は媒質1、媒質2ともに下記のように一致する。
\begin{cases}E_{1}=\dfrac{Q_{1}}{\varepsilon _{1}S}=\dfrac{Q}{\varepsilon _{1}\pi r}\cdot \dfrac{\varepsilon _{1}}{\varepsilon _{1}+\varepsilon _{2}}=\dfrac{Q}{\pi \left( \varepsilon _{1}+\varepsilon _{2}\right) r}\\ E_{2}=\dfrac{Q_{2}}{\varepsilon _{2}s}=\dfrac{Q}{\varepsilon_{2} \pi r}\cdot \dfrac{\varepsilon _{2}}{\varepsilon _{1}+\varepsilon _{2}}=\dfrac{Q}{\pi \left( \varepsilon _{1}+\varepsilon _{2}\right) r}\end{cases}
磁場の算出
磁束密度\(B\)が境界面において連続になる。
アンペールの法則を考える。円周路は、\(\pi r\)ずつ透磁率\(\mu_{1},\mu_{2}\)内に存在するので
\begin{eqnarray}B \cdot 2\pi r=\dfrac{\mu _{1}I}{2}+\dfrac{\mu _{2}I}{2} \\ B=\dfrac{\left( \mu _{1}+\mu _{2}\right) }{4\pi r}I \end{eqnarray}
これより、求める磁場\(H\)は
\begin{cases}H_{1}=\dfrac{B}{\mu _{1}}=\dfrac{\left( \mu _{1}+\mu _{2}\right) }{4\pi r\mu _{1}}I\\ H_{2}=\dfrac{B}{\mu _{2}}=\dfrac{\left( \mu _{1}+\mu _{2}\right) }{4\pi r\mu _{2}}I\end{cases}
最後に
本問に限らず、境界条件を活用して電場、磁場を求める問題は院試頻出です。参考になれば幸いです。