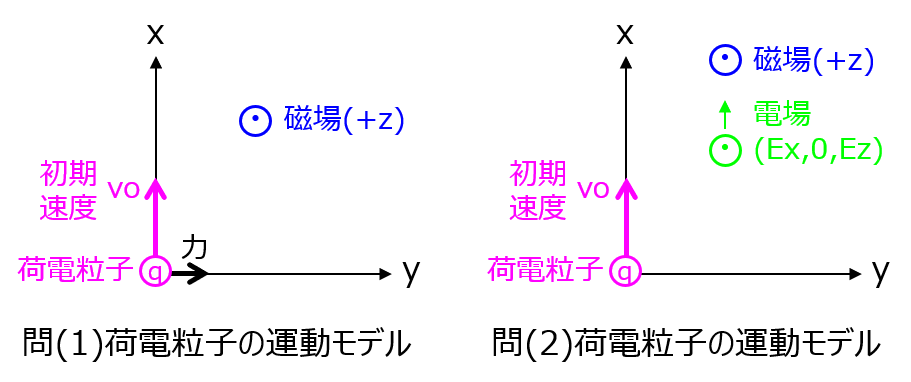
電場の無い一様の磁場中\(\boldsymbol{B}=B_{o}\widehat{\boldsymbol{z}}\)に荷電粒子をx軸方向に初速度\(v_{o}\)で打ち込む。
(1)その時の荷電粒子の運動について考えよ。なお、荷電粒子の電荷量は\(q\)、質量は\(m\)とする。
(2)y成分を持たない電場\(\boldsymbol{E}=(E_{x},0,E_{z})\)を(1)に追加で与えるとする。この時の荷電粒子の運動はどのようになるか。
荷電粒子とは
読んで字のごとく、電荷量\(q\)を持つ粒子を言います。電磁気学、量子力学など、様々な物理学問において現象を理解するために与える物理モデルに登場します。
簡単化のため、一般的に、一つの粒子のみについて論じることが多いです。本問も、一つだけの粒子に対する現象を深堀していきますが、数が増えても同じ傾向が出るため、一般性は損なわれません。
ローレンツ力と荷電粒子の運動
ローレンツ力とは、荷電粒子に働く電磁力を言います。
磁場ベクトルを\(\boldsymbol{v}\)、荷電粒子の速度ベクトルを\(\boldsymbol{v}\)とすると、発生する力\(\boldsymbol{F}\)は
\begin{aligned}\boldsymbol{F}=q(\boldsymbol{v}×\boldsymbol{B})\end{aligned}
となり、荷電粒子の運動方向と磁場の外積方向に力がかかります。
図示すると下記のようになり、円運動をし続けることが予想できます。
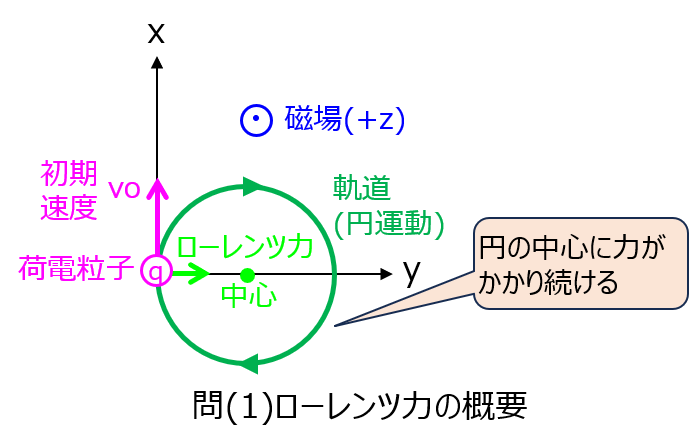
円運動をするときの実際の半径や、中心座標に関して問(1)で定量的に考えていきます。
また、電場\(\boldsymbol{E}\)もかかっているときの力は下記のようになります。
\begin{aligned}\boldsymbol{F}=q(\boldsymbol{E}+\boldsymbol{v}×\boldsymbol{B})\end{aligned}
磁場の成分は円運動に寄与し、電場の成分は一定の方向に移動し続けると予想できます。これは(2)で考えます。
解答例
基本的に、微分方程式を解くことで解決します。
\(e^{ax}\)型を仮定して解くことも可能ですが、問題(1)ではラプラス変換を用いて解きます。
(1)電場が無い状態での運動
運動方程式は
\begin{aligned}m\dfrac{d\boldsymbol{v}}{dt}=q\boldsymbol{v}×\boldsymbol{B}\end{aligned}
磁場はz方向で、荷電粒子は、x,y方向の運動をする。このため、上式をx,y,zの3方向に分解すると
\begin{cases}m\dfrac{dv_{x}}{dt}=qBv_{y} \\ m\dfrac{dv_{y}}{dt}=-qBv_{x} \\ m\dfrac{dv_{z}}{dt}=0 \end{cases}
これをラプラス変換すると、\(v_{x}(0)=v_{o}\)なので
\begin{cases}msV_{x}(s)-mv_{o}=qBV_{y}(s) \\ msV_{y}(s)=-qBV_{x}(s) \\ V_{z}(s)=0\end{cases}
第二式より、\(V_{y}(s)=-\dfrac{qB}{ms}V_{x}(s)\)。これを第一式に代入すると
\begin{aligned}\left(ms+\dfrac{(qb)^{2}}{ms}\right)V_{x}(s)=mv_{o}\end{aligned}
\begin{aligned}V_{x}(s)&=\dfrac{m^{2}v_{o}s}{(ms)^{2}+(qB)^{2}} \\ &=v_{o}\dfrac{s}{s^{2}+\left(\dfrac{qb}{m}\right)^{2}}\end{aligned}
これをラプラス逆変換すると
\begin{aligned}v_{x}(t)=v_{o}\cos\dfrac{qB}{m}t\end{aligned}
\(\omega=\dfrac{qB}{m}\)と置くと
\begin{aligned}v_{x}(t)=v_{o}\cos\omega t\end{aligned}
次に、y方向の速度\(v_{y}\)を考える。\(V_{x}(s)=-\dfrac{ms}{qB}\)を(5)式の第一式に代入し
\begin{aligned}\left(qB+\dfrac{(ms)^{2}}{qB}\right)V_{y}(s)=-mv_{o}\end{aligned}
\begin{aligned}V_{y}(s)=-\dfrac{qBmv_{o}}{(ms)^{2}+(qB)^{2}}\end{aligned}
\begin{aligned}V_{y}=\dfrac{\dfrac{qB}{m}}{s^{2}+\left(\dfrac{qB}{m}\right)^{2}}\end{aligned}
これをラプラス逆変換する。\(\omega=\dfrac{qB}{m}\)だから
\begin{aligned}v_{y}=-v_{o}\sin \omega t\end{aligned}
(9)式、(13)式が求める荷電粒子の運動(速度)である。
位置に関しては、それぞれ時間tで積分し、初期条件(x,y)=(0,0)を代入すれば良く
\begin{cases}x(t)=\dfrac{v_{o}}{\omega}\sin \omega t \\ y(t)=\dfrac{v_{o}}{\omega}(\cos \omega t -1)\end{cases}
上式を三角関数項とその他の項に分けて2乗すると
\begin{cases}x(t)^{2}=\left(\dfrac{v_{o}}{\omega}\sin \omega t \right)^{2} \\ \left(y(t)+\dfrac{v_{o}}{\omega}\right)^{2}=\left(\dfrac{v_{o}}{\omega}\cos \omega t \right)^{2}\end{cases}
上記、2つの式を足し合わせる。\(\sin^{2}\omega t+\cos^{2}\omega t=1\)だから
\begin{aligned}x(t)^{2}+\left(y(t)+\dfrac{v_{o}}{\omega}\right)^{2}=\left(\dfrac{v_{o}}{\omega} \right)^{2}\end{aligned}
よって、荷電粒子は(x,y)=(0,-vo/ω)を中心とする半径\(r=\dfrac{mv_{o}}{qB}\)の円運動を行う。
一定速度の円運動を継続するため、エネルギー的に増減無いことが分かります。
ラーモア半径(ラーマ半径)
前節により、荷電粒子は一定の半径
\begin{aligned}(r=\dfrac{mv_{o}}{qB}\end{aligned}
で円運動をし続けることが分かりました。これをラーモア半径と言います。
式に注目すると、下記の性質があることが分かります。
荷電粒子の各パラメータに対し、下記の依存性がある。
- 質量が大きいとき:半径が大きくなる。
- 初期速度が高いとき:半径が大きくなる。
- 電荷量が大きいとき:半径が小さくなる。
- 磁場が大きいとき:半径が小さくなる。
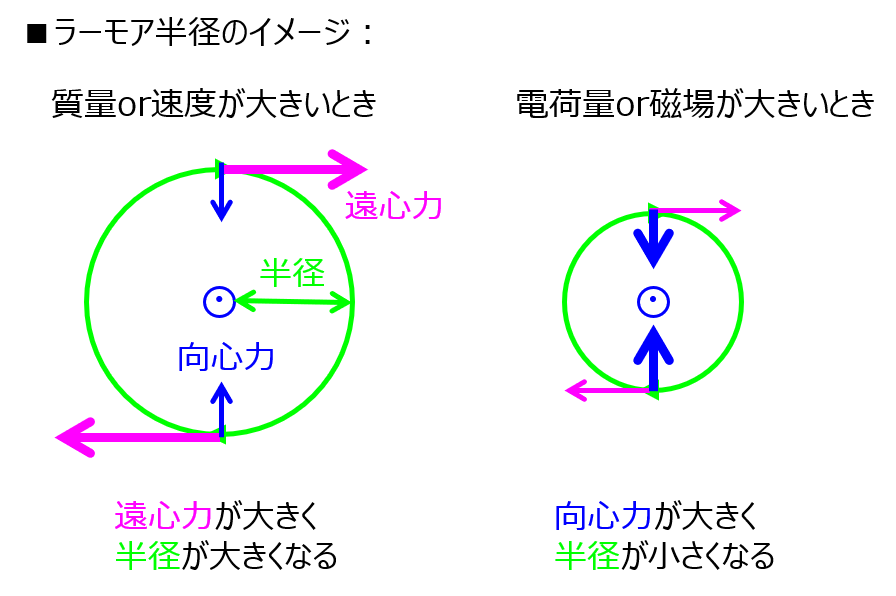
イメージになりますが、運動量mvが大きいほど、遠心力が大きくなるため、半径rが大きくなる方向になります。
一方で、電荷量や磁場が大きいときは、半径を大きくせずとも向心力を確保できるため、半径rは小さくなる方向に働きます。
(2)電場がある状態の荷電粒子の運動
計算が難しくなりますが、x,z方向の電場\(\boldsymbol{E}=(E_{x},0,E_{z})\)を与えた場合の振る舞いも考えます。
y方向に電場はかけていないので、y方向の運動方程式は変化せず、(4)式を参考にすると
\begin{cases}m\dfrac{dv_{x}}{dt}=qBv_{y}+qE_{x} \\ m\dfrac{dv_{y}}{dt}=-qBv_{x} \\ m\dfrac{dv_{z}}{dt}=qE_{z} \end{cases}
となります。第一式、第三式が変化します。
第三式は独立になっているので、そのまま時間で積分します。z方向の速度\(v_{z}\)は
\begin{aligned}v_{z}=\dfrac{qE_{z}}{m}t\end{aligned}
になります。(z方向の初期速度は0である前提です。)
一方で、第一式と第二式に関して考えます。(18)式を微分して
\begin{cases}m\dfrac{d^{2}v_{x}}{dt^{2}}=qB\dfrac{dv_{y}}{dt} \\ m\dfrac{d^{2}v_{y}}{dt^{2}}=-qB\dfrac{dv_{x}}{dt}\end{cases}
(20)式の右辺に(18)式を代入する。\(\omega=\dfrac{qB}{m}\)を考慮して
\begin{cases} \dfrac{d^{2}v_{x}}{dt^{2}}=-\omega^{2}v_{x} \\ \dfrac{d^{2}v_{y}}{dt^{2}}=-\omega^{2}\left(\dfrac{E_{x}}{B}+v_{y}\right)\end{cases}
\(E_{x},B\)は一定値なので、(21)式の第二式は下記のように書き直せる。
\begin{aligned}\dfrac{d^{2}}{dt^{2}}\left(\dfrac{E_{x}+v_{y}}{B}\right)=-\omega^{2}\left(\dfrac{E_{x}}{B}+v_{y}\right)\end{aligned}
2階微分し、右辺に\(-\omega\)が付いてカッコ内は同じになる項は指数関数であると考えられる。
よって、下記のような解になる。
\begin{cases}v_{x}=v_{o}e^{i\omega t} \\ v_{y}=-iv_{o}e^{i \omega t}-\dfrac{E_{x}}{B}\end{cases}
実数部を考慮すると、下記になる。
\begin{cases}v_{x}=v_{o}\cos \omega t \\ v_{y}=v_{o}\sin \omega t-\dfrac{E_{x}}{B}\end{cases}
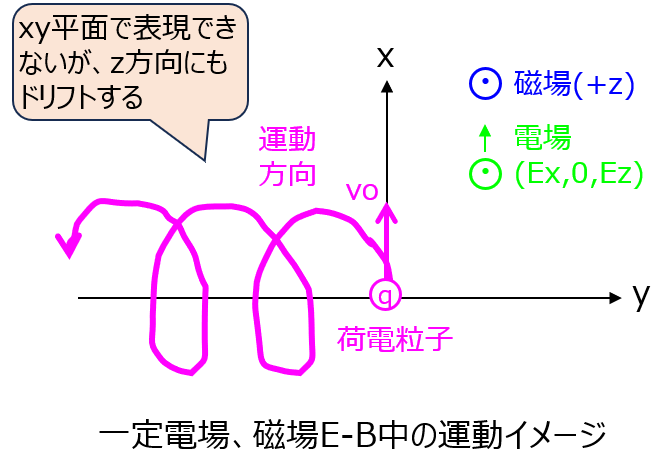
電場が与えられていない状態で発生する速度((9)式(13)式)と電場を与えた状態で発生する速度(24)式を比べてみます。x方向の運動には差が無いものの、y方向の運動では、ドリフト成分\(-\dfrac{E_{x}}{B}\)が発生することが分かりました。
このように、x,z方向の電場を与えた場合、-y方向のドリフトが発生します。
最後に
本問は、プラズマ工学の内容も含まれていますが、注釈を与えた上で電磁気学の院試で問われることがあります。
類題として経験しておくと、実際に出題されたとき、有利になります。是非知識として持っておきましょう。