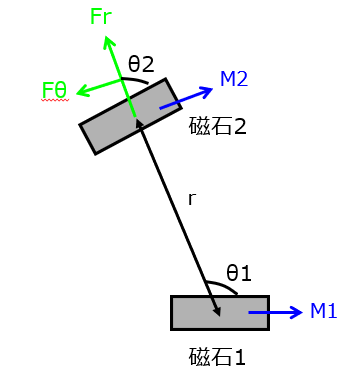
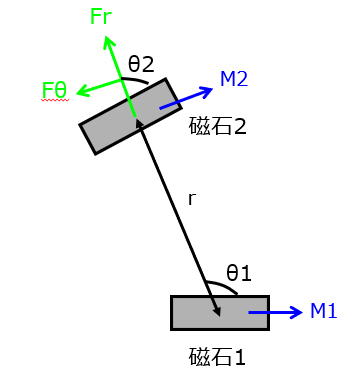
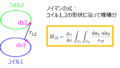磁気モーメント\(\boldsymbol{M_{1}},\boldsymbol{M_{2}}\)の磁石が下記の図のように置かれている。下記の問いに答えよ。
(1)磁石\(M_{1}\)による磁石\(M_{2}\)の位置エネルギー
(2)磁石\(M_{2}\)の\(r\)方向にに作用する力
(3)磁石\(M_{2}\)が受ける偶力モーメント
磁石に関するパラメータ
磁気双極子モーメントと磁位、磁場
電気双極子の場合と同じく、磁気モーメント\(\boldsymbol{M}\)を持つ磁石が\(r\)離れた位置の磁位\(\phi_{m}\)は下記で表されます。
\begin{aligned}\phi_{m}=\dfrac{\boldsymbol{M}・\boldsymbol{r}}{4 \pi \mu_{o}r^{3}}=\dfrac{M \cos \theta}{4 \pi \mu_{o}r^{2}}\end{aligned}
これを\(r,\theta\)で微分することで、位置\(r\)での磁界\(H_{r},H_{\theta}\)は
\begin{cases}H_{r}=-\dfrac{\partial \phi_{m}}{\partial r}=\dfrac{M \cos \theta}{2 \pi \mu_{o} r^{3}} \\ H_{\theta}=-\dfrac{1}{r}\dfrac{\partial \phi_{m}}{\partial \theta}=\dfrac{M \sin \theta}{4 \pi \mu_{o} r^{3}}\end{cases}
磁気モーメントと位置エネルギー
外部磁界\(\boldsymbol{H}\)の磁界の中に磁気モーメント\(\boldsymbol{M}\)を置いた時の位置エネルギー\(U\)は下記になります。
\begin{aligned}U=-\boldsymbol{M}・\boldsymbol{H}\end{aligned}
磁気モーメントと外部磁界の内積の負の成分に等しいです。
磁気モーメントは、負の磁荷から正の磁荷へ伸びるベクトルのため、無限遠から近づけていくとき、外部磁場との引力が発生します。これを相殺することから、負になる。ということですね。
磁石に働く力と偶力モーメント
ポテンシャルエネルギーが\(U\)のとき、一つの磁石にかかる力\(\boldsymbol{F}\)は
\begin{aligned}\boldsymbol{F}=-grad U=-grad(\boldsymbol{M}・\boldsymbol{H})\end{aligned}
これより、ある\(x\)方向にかかる力は
\begin{aligned}F_{x}=-\dfrac{\partial U}{\partial x}\end{aligned}
になります。磁石同士が距離r離れて正対している本問では、磁石に働く斥力(引力)になります。(同じく、\(\theta\)方向に微分すれば、
また、本問の系の場合、棒磁石にかかる偶力モーメント\(\boldsymbol{N}\)は周方向\(\theta\)にかかります。(偶力モーメントにより、棒磁石が物理的に回転する様をイメージすると分かりやすいです。)
よって、位置エネルギー\(U\)を\(\theta\)で微分することで
\begin{aligned}N_{\theta}=-\dfrac{\partial U}{\partial \theta}\end{aligned}
で表されます。この事実は(3)で使用します。
解答例
(1)位置エネルギー
磁石\(M_{1}\)から\(r\)離れた\(M_{2}\)に生じる磁界\(H_{1r},H_{1\theta}\)は、(2)式より
\begin{cases}H_{1r}=\dfrac{M_{1} \cos \theta_{1}}{2 \pi \mu_{o} r^{3}} \\ H_{\theta}=\dfrac{M_{1} \sin \theta_{1}}{4 \pi \mu_{o} r^{3}}\end{cases}
これより、磁石2の位置エネルギー\(U_{2}\)は
\begin{aligned}U_{2}&=-\boldsymbol{M_{2}}・\boldsymbol{H_{1}} \\ &=-M_{2}\cos \theta_{2}H_{1r}-M_{2}\cos (\theta_{2}+\pi/2)H_{1\theta} \\ &=-\dfrac{M_{1}M_{2}}{4 \pi r^{3}}(2\cos \theta_{1} \cos \theta_{2}-\sin \theta_{1} \sin\theta_{2})\end{aligned}
(2)磁石2に働く力
(5)式により、r方向に働く力\(F_{r}\)は
\begin{aligned}F_{r}&=-\dfrac{\partial U_{2}}{\partial r} \\ &=-\dfrac{3M_{1}M_{2}}{4 \pi r^{4}}(2\cos \theta_{1} \cos \theta_{2}-\sin \theta_{1} \sin\theta_{2})\end{aligned}
(3)磁石2の偶力モーメント
(6)式により、\(\theta\)方向に微分すれば良く
\begin{aligned}N_{\theta2}&=-\dfrac{\partial U_{2}}{\partial \theta_{2}} \\ &=-\dfrac{M_{1}M_{2}}{4 \pi r^{3}}(2\cos \theta_{1} \sin \theta_{2}-\sin \theta_{1} \cos\theta_{2})\end{aligned}
最後に
本問は、大阪公立大の院試で実際に出題されたことがあります。磁石に関する問題は殆どの大学の院試で殆ど出題されたことがありませんが、上記の大学を志望する場合は注意しましょう。