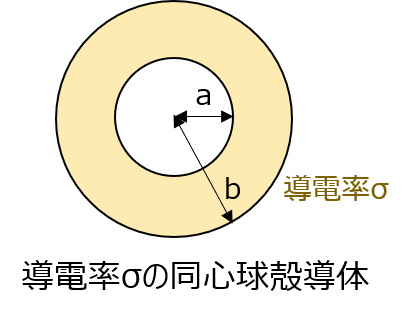
下記のように、内径\(a\)、外径\(b\)の同心球殻導体の間に導電率\(\sigma\)の媒質を満たすとき、媒質の電気抵抗\(R\)を求めよ。
なお、下記の式を用いて良い。
\begin{aligned}\Delta \phi=\dfrac{\partial \phi}{\partial r}\widehat{\boldsymbol{r}}+\dfrac{1}{r}\dfrac{\partial \phi}{\partial \theta}\widehat{\boldsymbol{\theta}}+\dfrac{1}{r\sin \theta}\dfrac{\partial \phi}{\partial \varphi}\widehat{\boldsymbol{\varphi}}\end{aligned}
電磁気学における電気回路パラメータ
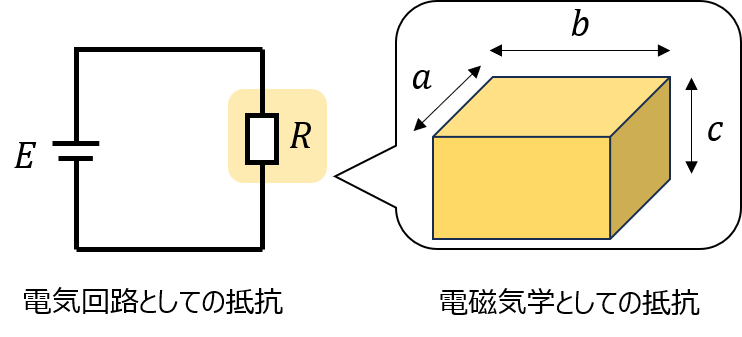
電気回路では、問題文で前提条件を与えられていることが多いです。一方で、電磁気学においては物質的な特徴に基づき、一段階ミクロな視点で考えます。
電磁気学における電気抵抗
高校物理でも出てくることがありますが、下記の式で表されます。
\begin{aligned}R=\dfrac{l}{\sigma S}\end{aligned}
\(l\)は導体の長さ、\(\sigma\)は導電率、\(S\)は導体の断面積です。電気回路では、Rだけ与えられて解くことが多いですが、電磁気学では上式の右辺のように分解して考えます。
注意点として、電流の流れる向きによってパラメータとして取る\(l\)、\(S\)の対応は変わります。
例えば、一辺の長さがa,b,cの直方体に電流を流す場合を考えましょう。
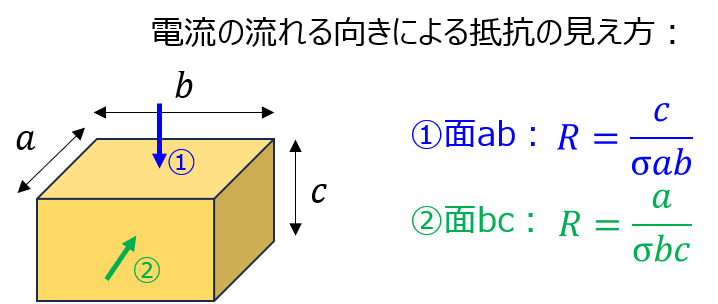
a,bの面から流すときは\(S=ab,l=c\)になりますが、b,cの面からの場合だと\(S=ac,l=b\)になり、抵抗Rの結果は変わります。
このため、電磁気学で抵抗値の算出を求められたときは、物質内を流れる電流の向きに注意する必要があります。
電磁気学における電流
電流についても、電磁気学では下記の式を用います。
\begin{aligned}\boldsymbol{i}=\sigma \boldsymbol{E}\end{aligned}
\(\boldsymbol{i}\)は電流密度です。導電率が有限の導体内で電場が発生しているから、これを電流として考える。という立場ですね。
もし、真空だと導電率は極めて低いです。このため、\(E\)は一定量存在するが、\(i\)は殆ど存在しない。という考え方ができ、イメージと合います。
電位は電場の線積分で求められますが、上式により電流密度の線積分でも考えることができます。本記事のように、導電率だけパラメータとして与えられている問題に対し、この考え方を用います。
静電容量との関係
問題文で与えた導体を誘電率\(\varepsilon\)コンデンサとして見た時、\(Q=CV\)とオームの法則の関係から下記の式変形が出来ます。
\begin{aligned}C=\dfrac{Q}{V}=\dfrac{\varepsilon}{\sigma}\dfrac{I}{V}=\dfrac{\varepsilon}{\sigma}\dfrac{1}{R}\end{aligned}
よって、
\begin{aligned}CR=\dfrac{\varepsilon}{\sigma}\end{aligned}
の関係式が成立します。本式から、静電容量\(C\)が求まれば、実は抵抗\(R\)も求められることが分かります。(※導電率と誘電率は既知)
解答例
前節までの説明から、2通りの解き方で抵抗Rを算出することができます。
- 電流密度\(i\)を設定し、球殻間の電位差\(V\)を求める。オームの法則\(V=IR\)より、未知数Rを決定。
- 静電容量を求め、(5)式に代入して未知数Rを決定
解答方法1:オームの法則
球の中心から\(r (a<r<b)\)離れた地点での電流密度を\(i\)とする。内径から外径に対し、放射状に電流が流れているので、求める電流Iは
\begin{aligned}I=i*4 \pi r^{2}\end{aligned}
この式から、電流密度\(i\)は下記になる。
\begin{aligned}i=\dfrac{I}{4 \pi r^{2}}\end{aligned}
\(\boldsymbol{i}=\sigma \boldsymbol{E}\)を変形すると、電位との関係式
\begin{aligned}\boldsymbol{i}=\sigma \boldsymbol{E}=-\sigma \Delta \phi = -\sigma \dfrac{d \phi}{dr} \widehat{\boldsymbol{r}}\end{aligned}
が微分方程式として導かれる。これを変数分離の方法で解くと
\begin{aligned}\dfrac{d \phi}{dr}=-\dfrac{I}{4 \pi \sigma r^{2}}\end{aligned}
\begin{aligned}\phi(r)=\dfrac{I}{4 \pi \sigma r}+C\end{aligned}
ここで、Cは定数である。この式を用いると、内球と外球の電位差Vは
\begin{aligned}V&=\phi(a)-\phi(b) \\ &=\dfrac{I}{4 \pi \sigma} \left( \dfrac{1}{a}-\dfrac{1}{b} \right)\end{aligned}
これより、求める電気抵抗Rは
\begin{aligned}R=\dfrac{V}{I}=\dfrac{1}{4 \pi \sigma} \left( \dfrac{1}{a}-\dfrac{1}{b} \right)\end{aligned}
解答方法2:静電容量との関係
まず、同心球殻コンデンサの静電容量を考える。
内球に電荷Q、外球に-Q設定した時、球殻間(a<r<b)の電場Eは
\begin{aligned}E=\dfrac{Q}{4 \pi \varepsilon_{o} r^{2}}\end{aligned}
これを区間[b,a]で積分することで、電位差Vは
\begin{aligned}V=\dfrac{Q}{4 \pi \varepsilon_{o} }\left( \dfrac{1}{a}-\dfrac{1}{b} \right)\end{aligned}
\(Q=CV\)より、求める静電容量は
\begin{aligned}C=\dfrac{ 4 \pi \varepsilon_{o}}{\dfrac{1}{a}-\dfrac{1}{b}}\end{aligned}
(5)式の誘電率を\(\varepsilon_{o}\)に置き換えることに注意し、上記の結果を代入すると、同じく(12)式を得る。
最後に
本問は、東工大、九大で出題されることがあります。2通りの計算で答えが出せるため、片方の方法で出した場合も、妥当性の検算をするためにもう一方も出来るようになっておくことをオススメします。
個人的には、特に指定が無ければ解答方法1でオーソドックスに解いて、検算に方法2が良いと思います。