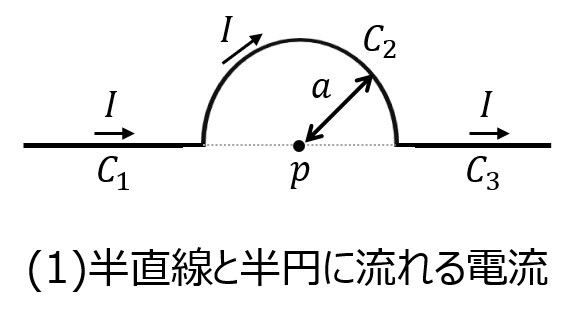
(1)下記のように、半直線\(C_{1},C_{3}\)と半円\(C_{2}\)に電流が流れている。
半円の中心軸上の磁束密度\(B\)を求めよ。
(2)下記の導体で、アンペールの法則を適用できる条件はどれか。全て答えよ。
なお、円環電流及びソレノイドには電流\(I\)が流れているとし、無限長ソレノイドの電流密度を\(J\)とする。
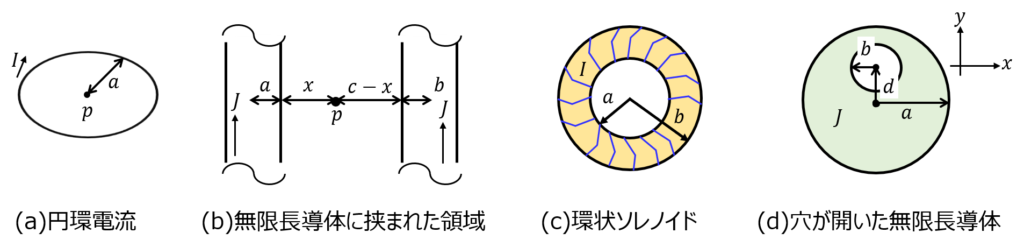
(a) 半径aの円環電流
(b) 半径a、半径bの無限長導体に挟まれている点P
(c) 内半径a、外半径b、高さ1、巻き数Nの環状ソレノイド
(d) 半径aの導体の中心からy方向にd離れた位置に半径bの穴が開いた無限長導体
はじめに
磁束密度を求める際、ビオサバールの法則とアンペールの法則を用いたことがあると思います。
問題経験が増えてくると、問題を解くことがパターン化し、無意識のうちに両者を使い分けている人が多いです。
ですが、計算していく上で気を付けなければならないことがあります。
本記事で覚えたいこと
- \(d\boldsymbol{B}=\dfrac{\mu _{0}}{4\pi }\dfrac{Id\boldsymbol{s}\times \boldsymbol{r}}{r^{2}}\)で与えられ、電流ベクトル\(d\boldsymbol{s}\)と目標とする地点Pへのベクトル\(\boldsymbol{r}\)の外積で求められる
- 電流ベクトルと目標点Pが同じベクトルの向きの場合、外積=0である。このため、磁場は発生しない。
2.が本記事で主張したいことです。
1.の式の定義から明らかですが、スカラーに変換した式で向きを無視し、機械的に計算すると間違った結果になってしまいます。
逆に、これさえ気を付ければ、後は計算ミスに気を付けるのみです。
- \(\int _{C}\boldsymbol{B} d\boldsymbol{s}=\mu_{0} I\)で表される。
- 取る閉路\(C\)上の磁場が一定の場合、適用可能
アンペールの法則の法則の意味は以下になります。
取った閉路上の磁場が一定値ならば、閉路内に存在する電流値を閉路の長さで割った値が磁場\(H\)に等しい。
ですので、閉路C上にある磁場が一定値であることが重要になります。本問では、どの場合が当てはまるのでしょうか。
解答例
(1) ビオサバールの法則
電流ベクトルと点Pに対する向きが同じのため、積分路\(C_{1},C_{3}\)から発生する磁束密度は0。
半円積分路\(C_{2}\)から発生する磁束密度を考える。
微小線分から発生する磁場は
\begin{aligned}dB=-\dfrac{\mu _{0}Ia}{4\pi a^{2}}d\theta \\ \end{aligned}
これを区間\(0≦\theta≦\pi\)で積分し
\begin{aligned}B&=-\int ^{\pi }_{0} \dfrac {\mu_{0}I}{4\pi a}d\theta \\
&=-\dfrac{\mu _{0}I}{4a}\end{aligned}
(2)アンペールの法則
(a)半径aの円環電流から発生する磁場
点P周りに閉路を取ったとき、半径方向の磁場分布が区間によって異なる。
対称な磁場分布とならないため、アンペールの法則は適用できない。
ビオサバールの法則で磁束密度を求める。式(4)の積分範囲を\(2 \pi\)に換算すれば良いので
\begin{aligned}B=-\dfrac{\mu _{0}I}{2a}\end{aligned}
(b)半径a、半径bの無限長導体に挟まれている点P
無限長導体のため、アンペールの法則を適用可能。
\begin{eqnarray}B =\dfrac{\mu_{0} \cdot a^{2}J}{2x}+\dfrac{\mu _{0}a^{2}J}{2\left( c-x\right) }\end{eqnarray}
※有限長ソレノイドの場合はアンペールの法則を適用できません。(a)の円環電流の計算を巻き数分適用する必要があります。
(c) 内半径a、外半径b、高さ1、巻き数Nの環状ソレノイド
環状ソレノイド内は対称な磁場分布となるため、アンペールの法則を適用可能。
\begin{eqnarray}B=\dfrac{\mu _{0}NI}{2\pi r}\end{eqnarray}
(d) 半径aの導体の一部に半径bの穴が開いた無限長導体
これは特殊ケースです。
以前の記事でも紹介しましたが、穴の開いた導体から発生する磁場を計算する際は、以下の考え方を利用します。
- 穴の無い場合で求めたいパラメータを算出する
- 穴のある部分を、物理量を逆にし求めたいパラメータを算出する
この考えを適用すると、(b)のようにアンペールの法則を使用できます。
まず、穴の無い場合は
\begin{aligned}B_{1}=\dfrac{J\pi r^{2}\mu _{0}}{2\pi r}=\dfrac{\mu_{0} J}{2}\sqrt{x^{2}+y^{2}}\end{aligned}
次に、穴のある部分について、\(y’=y-d\)とすれば良いので
\begin{aligned}B_{2}=-\dfrac{\mu_{0} J}{2}\sqrt{x^{2}+\left( y-d\right) ^{2}}\end{aligned}
これより、求める磁場は、\(B_{1},B_{2}\)を足し合わせると良いので
\begin{aligned}B=\dfrac{\mu_{0} J}{2}(\sqrt{x^{2}+y^{2}}-\sqrt{x^{2}+\left( y-d\right) ^{2}})\end{aligned}
最後に
本記事で磁界計算の基本を紹介しました。問題集にて、難しめの問題を経験すると良いと思います。
参考文献
詳解電磁気学演習 P243:後藤 憲一(著)、山崎 修一郎(著)