(1)下記のベクトル界の中で、静電界を表すものを答えよ。
\begin{cases}E_{1}=(3y,3x+y+5z,5y) \\ E_{2}=(x^{2}-y^{2},4,2xy) \\ E_{3}=(x+y,-x+y,-2z)\end{cases}
(2)(1)で与えたベクトル界の中で、ラプラス方程式を満たすものを答えよ。
静電界とは
- 時間変動しない電場\(E(t)=0\)
- エネルギーが保存する場
- 渦が発生しない。\(rot\boldsymbol{E}=0\)
1.ばかり言われていますが、電磁気学を根本から理解する上で、2.3も必要な性質です。
静電界の場合、ある地点\(r\)における電場は時間項t抜きで\(\boldsymbol{E(r)}\)で表されることから、電位Vは
\begin{aligned}V=-\int^{r}_{∞}\boldsymbol{E(r)}・d\boldsymbol{r}=const\end{aligned}
となる。よって、任意の時間で電位は変わらないことから、エネルギーは保存すると言えます。
しかし、時間項が付属する際は、(1)式に変数が付いてしまい、時間によって変化することが分かります。よって、静電界の場合のみ、エネルギーは保存します。
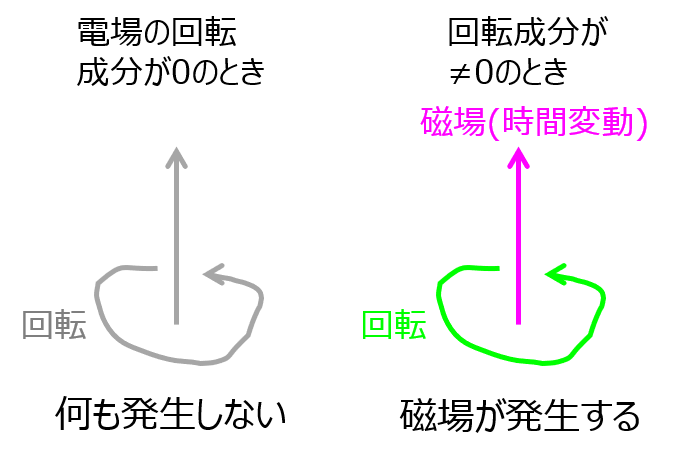
また、静電界の場合、回転成分も発生しません。
もし回転成分が非零ならば、マクスウェル方程式
\begin{aligned}rot\boldsymbol{E}=-\dfrac{\partial \boldsymbol{B}}{\partial t}≠0\end{aligned}
も非零になるから、時間変動する磁場が発生します。磁場の発生源は電流ですから、時間変動する電流(電場)も存在すると解釈できます。背理法により、静電場であるためには回転成分が0である必要が分かりました。
静電界と電位
(1)式のように、ベクトル場の線積分で電位\(V\)を求めることができますが、他の方法でも電位を考えることができます。
前章より、静電界であるとき、\(rot\boldsymbol{E}=0\)であることが分かりました。あるポテンシャルの勾配(grad)に回転(rot)を取った場合、一般的に\(rot(grad \boldsymbol{A})=0\)であることから、定数のポテンシャル\(V\)を設定すると
\begin{aligned}\boldsymbol{E}=grad V\end{aligned}
と表記できます。電位の定義で示すこともできますが、ベクトル関数を解くことでも電位を導くことができました。
ラプラス方程式とは
ポアソン方程式の右辺が0のとき、ラプラス方程式と言います。
\begin{aligned}\Delta V=\dfrac{\rho}{\varepsilon_{o}}\end{aligned}
\begin{aligned}\Delta V=0\end{aligned}
ラプラス方程式を満たす条件
電場の発散\(div\)が0であることです。
これは、マクスウェル方程式
\begin{aligned}div\boldsymbol{E}=\dfrac{\rho}{\varepsilon_{o}}=0\end{aligned}
になることから、ポアソン方程式(5)式に代入すると、ラプラス方程式(6)式になることが分かります。
また、発散が0である物理的意味は、ある閉曲面から染み出す場が0だと言うことです。これは、電場が0であることを意味し、発生源の電荷\(\rho\)も0になることが分かります。
解答例
(1)ベクトル関数の計算
\(E_{1}=(3y,3x+y+5z,5y)\)について、回転\(rot\)を取って
\begin{aligned}rot\boldsymbol{E_{1}}&=\left(\dfrac{\partial}{\partial y}5y-\dfrac{\partial}{\partial z}(3x+y+5z),\dfrac{\partial}{\partial x}5y-\dfrac{\partial}{\partial z}5y,\dfrac{\partial}{\partial x}(3x+y+5z)-\dfrac{\partial}{\partial y}3y\right) \\ &=(5-5,0,3-3) \\ &=(0,0,0)\end{aligned}
よって、\(E_{1}\)は静電場である。
\(E_{2}=(x^{2}-y^{2},4,2xy)\)について
\begin{aligned}rot\boldsymbol{E_{1}}&=\left(\dfrac{\partial}{\partial y}2xy-\dfrac{\partial}{\partial z}4,-\dfrac{\partial}{\partial x}2xy+\dfrac{\partial}{\partial z}(x^{2}-y^{2}),\dfrac{\partial}{\partial x}(x^{2}-y^{2})-\dfrac{\partial}{\partial y}4\right) \\ &=(2x,-2y,2x)\end{aligned}
回転は非零であるため、\(E_{2}\)は静電場ではない。
\(E_{3}=(x+y,-x+y,-2z)\)について
\begin{aligned}rot\boldsymbol{E_{3}}&=\left(\dfrac{\partial}{\partial y}(-2z)-\dfrac{\partial}{\partial z}(-x+y),-\dfrac{\partial}{\partial x}(-2z)+\dfrac{\partial}{\partial z}(x+y),\dfrac{\partial}{\partial x}(-x+y)-\dfrac{\partial}{\partial y}(x+y)\right) \\ &=(0,0,-2)\end{aligned}
\(E_{3}\)は静電場ではない。
(2)ラプラス方程式で表される関数
前節より、発散が0のベクトル関数が条件を満たします。
\(E_{1}=(3y,3x+y+5z,5y)\)について、
\begin{aligned}div\boldsymbol{E_{1}}=0+1+0=1\end{aligned}
\(E_{2}=(x^{2}-y^{2},4,2xy)\)について
\begin{aligned}div\boldsymbol{E_{2}}=2x+0+0=2x\end{aligned}
\(E_{3}=(x+y,-x+y,-2z)\)について
\begin{aligned}div\boldsymbol{E_{3}}=1+1-2=0\end{aligned}
よって、\(E_{3}\)がラプラス方程式を満たす。