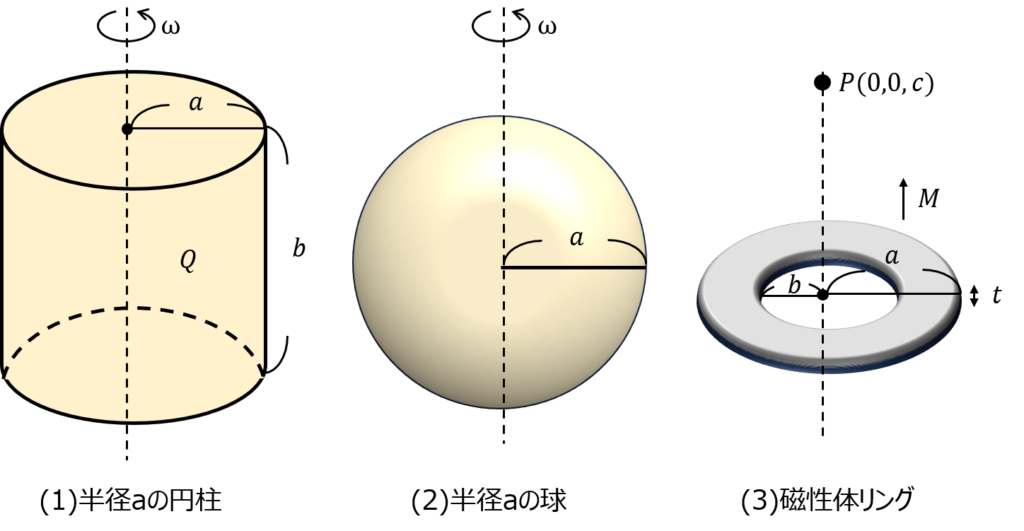
【問題】下記の導体が総電荷\(Q\)で一様に帯電している。中心軸周りに一定の角速度\(\omega\)で回転するとき、(1)(2)それぞれの場合の磁気モーメントを求めよ。
(1)半径\(a\)長さ\(b\)の円柱導体
(2)半径\(a\)の導体球
(3),(1)(2)の考え方を用いて、磁性体中空薄板リングの中心軸上の点Pで発生する磁束密度を求めよ。ただし、外周の半径を\(a\)、内周の半径を\(b\)とする。
なお、半径\(a\)の円環電流が、中心軸から\(z\)離れた方向に作る磁束密度は下記で与えられる。
\begin{eqnarray}B=\dfrac{\mu_{0} Ia^{2}}{2\left( a^{2}+z^{2}\right) ^{\frac{3}{2}}}\end{eqnarray}
はじめに
本問を勉強すると、磁性体から発生する磁界解析を行う際に基本となる考え方を学ぶことができます。ある一様な磁化ベクトル\(M\)で中心軸方向に一様に磁化された磁性体から発生する磁場を求める際によく使います。
磁気双極子\(m\)から磁位を求め、勾配を取ることで磁束密度\(B\)を算出する方法もあります。ただ、工学部の院試ではあまりこの方法は出題されません。(ミクロな視点での解き方なので、理学部の院試では出てくるかもしれませんが・・)
代わりに、磁化ベクトルと磁化電流密度の関係式:\begin{eqnarray}rot \boldsymbol{M}=i_{m}\end{eqnarray}
を利用し、磁化ベクトルを等価な電流\(\boldsymbol{i_{m}}\)に置き換えて、目標となる地点の磁場を求めることがあります。
本問を通して抑えたいこと
- 磁化ベクトルの回転を取ると、疑似的に電流が流れているとみなせる(式(2))
- 逆に、円環電流が流れている導体には、磁化ベクトルが等価的に発生していると解釈できる
- 電荷の面密度をσとすると、電流Iは、σω/2π = σf で表すことができる
- \(m=IS\)より、ある区間の磁気モーメントを求め、導体全体の区間を積分し、全体の磁気モーメントを求める
磁化ベクトルは、単位体積当たりの磁気モーメントを示します。よって、磁化ベクトルを積分すると、磁気モーメントを求めることができます。
式(2)は、考える対象の物体が磁性体でなくとも、円環電流が流れていれば等価的に磁化ベクトルが発生していると解釈できます。この考え方を(1)(2)で使用します。
例として、(1)は、微小区間\(dz\)における磁気モーメントを\(m=IS\)を用いて導出し、0~z~bの範囲で積分して求めます。
(3)では、円環電流から発生する中心軸上の磁場の式を、磁性体の場合の流用方法について記載します。
解答例
(1) 回転円柱の磁気モーメント
導体の面密度は、側面の面積が\(2 \pi a b\)より\begin{eqnarray}\sigma_{1}=\dfrac{Q}{2\pi a b}\end{eqnarray}
このとき、微小区間\(dz\)に流れる電流は、円環の長さが\(2 \pi a\)であるので \begin{eqnarray}di_{1}=\dfrac{\omega}{2 \pi} \sigma 2 \pi a dz=\dfrac{\omega Q}{2 \pi b}\end{eqnarray}
これより、微小区間\(dz\)における磁気モーメントは\(m=IS\)の関係と、\(S=\pi a^{2}\)より
\begin{eqnarray}dm_{1}=\pi a^2 di_{1}=\dfrac{\omega a^{2} Q}{2b}dz\end{eqnarray}
これを、区間\(0≦z≦b\)で積分し、全体の磁気モーメント\(m_{1}\)は
\begin{eqnarray}m_{1}=\int_{0}^{b} \pi a^2 di_{1}=\int_{0}^{b}\dfrac{\omega a^{2} Q}{2b}dz=\dfrac{\omega a^{2} Q}{2}\end{eqnarray}
(2)回転球の磁気モーメント
(1)と同じくして、微小区間\(ad\theta\)における面密度、電流は
\begin{align}&\omega_{2}=\dfrac{Q}{4 \pi a^{2}} \\ &di_{2}=\dfrac{\omega}{2 \pi} \sigma 2\pi a \sin\theta a d\theta \\ &dm_{2}=\pi (a \sin\theta)^{2} di_{2}=\dfrac{a^{2}}{4}Q \omega \sin^{3}\theta d\theta \end{align}
これを区間\(0≦\theta≦\pi\)で積分することにより、求める磁気モーメントは
\begin{eqnarray}m_{2}=\dfrac{a^{2}}{4}Q\omega \int _{0}^{\pi }\sin ^{3}\theta d\theta \end{eqnarray}
3倍角の公式より
\begin{aligned}m_{2}&=\dfrac{a^{2}}{4}Q\omega \int _{0}^{\pi }\left( \dfrac{3}{4}\sin \theta -\dfrac{\sin ^{3}\theta }{4}\right) d\theta \\ &=\dfrac{a^{2}}{4}Q\omega \left[ -\dfrac{3}{4}\cos \theta +\dfrac{1}{12}\cos 3\theta \right] _{0}^{\pi }\\ &=\dfrac{a^{2}}{4}Q\omega \left( -\dfrac{3}{4}\left( -2\right) +\dfrac{1}{12}\cdot \left( -2\right) \right) \\ &=\dfrac{a^{2}Q\omega}{3}\end{aligned}
(3) 磁性体中空リングから発生する中心軸上の磁束密度
本問に限らないですが、どこか一部分に穴が開いている物体に対しての考え方は以下になります。
- 穴の無い場合で求めたいパラメータを算出する
- 穴のある部分を、物理量を逆にし求めたいパラメータを算出する
- 1.2の結果を足し合わせ、求めたい結果を算出する

電気回路でよく使用する重ね合わせの理を、電磁気学においても使用します。
本問の場合だと、まず半径aの穴の無い円盤を考え、そこから点Pに発生する磁束密度\(B_{a}\)を考えます。
(1)(2)より、ある磁気モーメントと等価になる円環電流(磁化電流)の関係式が分かりました。単位体積当たりの磁気モーメントは磁化ベクトル\(M\)で表されます。この部分で等価になる電流値は、\(|I|=|M×n|=|M|\)になる。本問の場合、薄板の厚さは\(t\)より、\(I=Mt\)になる。
与えられた式に、この結果をを代入し、
\begin{eqnarray}B_{a}=\dfrac{\mu_{0}Mta^{2}}{2(a^{2}+c^{2})^{\frac{3}{2}}}\end{eqnarray}
次に、逆向きの磁化ベクトルを持つ半径bの円盤を考える。与えられた式の符号を逆転し
\begin{eqnarray}B_{b}=-\dfrac{\mu_{0}Mtb^{2}}{2(b^{2}+c^{2})^{\frac{3}{2}}}\end{eqnarray}
よって、点Pで発生する磁束密度は、式(12)(13)を足し合わせ
\begin{eqnarray}B=\dfrac{\mu _{0}Mt}{2}\left( \dfrac{a^{2}}{\left( a^{2}+c^{2}\right) }-\dfrac{b^{2}}{\left( b^{2}+c^{2}\right) }\right)\end{eqnarray}
最後に
本問は、磁性体に対する理解を深めるに最適な問題です。単純に解くことも大事ですが、その結果から読み解ける事実を自身で考察すると良いと思います。
参考文献
1.電磁気学演習 山村 泰道(著) P79
2.新しい電磁気学 太田 昭男(著) P153