【量子力学】トンネル効果の説明と反射率、透過率の導出と説明

トンネル効果とは
トンネル効果の各パラメータの導出
最後に

トンネル効果とは

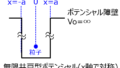
粒子がポテンシャル障壁を確率的に通過する現象を言います。例えば、ポテンシャル障壁$V_{o}$に対し、エネルギー$E$を持つ粒子が入射するとします。

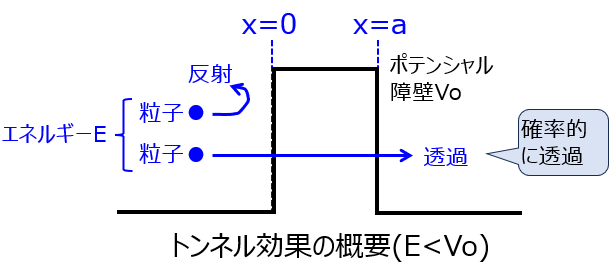
$E<V_{o}$の場合、古典力学の視点では、粒子は透過できず、反射率1になります。一方で、シュレーディンガー方程式を用いる量子力学の場合、ポテンシャル障壁内部で波動関数は0にならず、透過できる粒子が存在します。

本現象は、電子をはじめとするミクロな粒子の物性を考える上で必要な視点です。特に、半導体を微細化していく上で用います。隣の系と十分に距離が離れていれば電子は透過しませんが、微細化が進み、系が近くになるにつれて透過する電子が多くなり、ノイズになってしまいます。この現象が、近年の微細化の進捗状況に影響を与えています。

このように、工学分野と密接に関係のある分野で、院試でも多数の出題があります。本記事では、よく問われる事項を下記にまとめます。

トンネル効果の各パラメータの導出

冒頭と同じく、粒子のエネルギーがポテンシャル障壁よりも小さい$E<V_{o}$の場合を考えます。

ポテンシャル障壁は$0<x<a$に存在する場合、

最終的には、記事の表題通り透過率を求めます。透過率は、ポテンシャル障壁に入射する波の振幅と、ポテンシャル障壁を透過した後の領域の振幅の比で求められます。

一方で、振幅を求めるためには波動関数を考えねばなりません。波動関数を求めるためにはシュレーディンガー方程式を解くことが必要ですので、まずそこから解説します。

シュレーディンガー方程式と波動関数

シュレーディンガー方程式は下記のようになります。

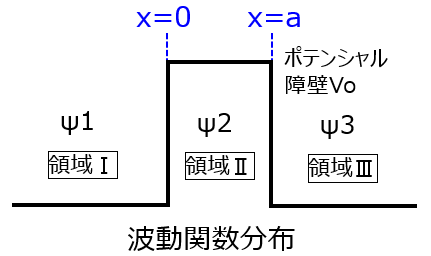
領域Ⅰ $x<0$

\begin{aligned}\frac{\hbar^2}{2m} \frac{d^2}{dx^2} \psi_I(x) = E \psi_I(x)\end{aligned}

\begin{aligned}\frac{d^2}{dx^2} \psi_I(x) = -\frac{2mE}{\hbar^2} \psi_I(x)\end{aligned}

$k_1 = \sqrt{\frac{2mE}{\hbar^2}}$とすると、一般解は

\begin{aligned}\psi_I(x) = A e^{ik_1 x} + B e^{-ik_1 x}\end{aligned}

$A$に関する項は入射波成分、$B$は反射波成分を表しています。

領域Ⅱ $0<x<a$

\begin{aligned}\frac{d^2}{dx^2} \psi_{II}(x) = \frac{2m(V_{o} – E)}{\hbar^2} \psi_{II}(x)\end{aligned}

$\kappa = \sqrt{\frac{2m(V_{o} – E)}{\hbar^2}}$とおくと、一般解は

\begin{aligned}\psi_{II}(x) = C e^{\kappa x} + D e^{-\kappa x}\end{aligned}

領域Ⅲ $x>a$

ポテンシャル障壁が無いため、領域Ⅰと同じシュレーディンガー方程式になります。同じ方法で波動関数を求められますが、反射波成分は存在しないです。入射波成分のみ考えれば良いため

\begin{aligned}\psi_{III}(x) = F e^{ik_1 x}\end{aligned}

境界条件

前節にて、各領域の波動関数は求まりましたが、未知数が$A,B,C,D,F$の5個あります。最終的には、$A,F$の2乗の比$\frac{|F^{2}|}{|A^{2}|}$で透過率が求められますが、他の未知数$B,C,D$を消去するための制約条件が必要です。これは、$x=0,a$の境界条件を考えることで達成できます。

(3)(4)(6)式において、境界条件を考えます。波動関数とその導関数が連続であるため

x=0における境界条件は

$\psi_I(0) = \psi_{II}(0)$
$$A e^{ik_1 \cdot 0} + B e^{-ik_1 \cdot 0} = C e^{\kappa \cdot 0} + D e^{-\kappa \cdot 0}$$
$$A + B = C + D $$

$\frac{d}{dx}\psi_I(0) = \frac{d}{dx}\psi_{II}(0)$
$$ik_1 A e^{ik_1 \cdot 0} – ik_1 B e^{-ik_1 \cdot 0} = \kappa C e^{\kappa \cdot 0} – \kappa D e^{-\kappa \cdot 0}$$
$$ik_1 (A – B) = \kappa (C – D)$$

x=aにおける境界条件は

$\psi_{II}(a) = \psi_{III}(a)$
$$C e^{\kappa a} + D e^{-\kappa a} = F e^{ik_1 a}$$

$\frac{d}{dx}\psi_{II}(a) = \frac{d}{dx}\psi_{III}(a)$
$$\kappa C e^{\kappa a} – \kappa D e^{-\kappa a} = ik_1 F e^{ik_1 a} $$

透過率の計算

境界条件で求められた関係式を用いて、AとFの関係式を導きます。

まず、式(11)と式(12)を用いて、$C$ と $D$ を $F$ を使って表します。

式(11)の両辺に $\kappa$ を掛けたものと式(12)を足し合わせます。
$$ \kappa(C e^{\kappa a} + D e^{-\kappa a}) + (\kappa C e^{\kappa a} – \kappa D e^{-\kappa a}) = \kappa F e^{ik_1 a} + ik_1 F e^{ik_1 a} $$
$$ 2\kappa C e^{\kappa a} = (\kappa + ik_1) F e^{ik_1 a} $$
$$ C = \frac{\kappa + ik_1}{2\kappa} e^{(ik_1 – \kappa)a} F $$

次に、式(11)の両辺に $\kappa$ を掛けたものから式(12)を引きます。
$$ \kappa(C e^{\kappa a} + D e^{-\kappa a}) – (\kappa C e^{\kappa a} – \kappa D e^{-\kappa a}) = \kappa F e^{ik_1 a} – ik_1 F e^{ik_1 a} $$
$$ 2\kappa D e^{-\kappa a} = (\kappa – ik_1) F e^{ik_1 a} $$
$$ D = \frac{\kappa – ik_1}{2\kappa} e^{(ik_1 + \kappa)a} F $$

次に、式(8)と式(10)を用いて、$A$ と $B$ を $C$ と $D$ を使って表します。

式(8)と式(10)の両辺を $ik_1$ で割ったものを足し合わせます。
$$ (A + B) + (A – B) = (C + D) + \frac{\kappa}{ik_1}(C – D) $$
$$ 2A = C \left(1 + \frac{\kappa}{ik_1}\right) + D \left(1 – \frac{\kappa}{ik_1}\right) $$
$$ 2A = C \frac{ik_1 + \kappa}{ik_1} + D \frac{ik_1 – \kappa}{ik_1} $$

式(8)から式(10)の両辺を $ik_1$ で割ったものを引きます。
$$ (A + B) – (A – B) = (C + D) – \frac{\kappa}{ik_1}(C – D) $$
$$ 2B = C \left(1 – \frac{\kappa}{ik_1}\right) + D \left(1 + \frac{\kappa}{ik_1}\right) $$
$$ 2B = C \frac{ik_1 – \kappa}{ik_1} + D \frac{ik_1 + \kappa}{ik_1} $$

最後に、式(5)と式(6)を式(7)に代入して、$A$ を $F$ で表します。

$$ 2A = \frac{ik_1 + \kappa}{ik_1} \left( \frac{\kappa + ik_1}{2\kappa} e^{(ik_1 – \kappa)a} F \right) + \frac{ik_1 – \kappa}{ik_1} \left( \frac{\kappa – ik_1}{2\kappa} e^{(ik_1 + \kappa)a} F \right) $$
$$ 2A = \frac{(ik_1 + \kappa)^2}{2ik_1\kappa} e^{(ik_1 – \kappa)a} F + \frac{(ik_1 – \kappa)(\kappa – ik_1)}{2ik_1\kappa} e^{(ik_1 + \kappa)a} F $$
ここで、$(ik_1 – \kappa)(\kappa – ik_1) = – (ik_1 – \kappa)^2$ であることに注意します。
$$ 2A = \frac{F}{2ik_1\kappa} \left[ (ik_1 + \kappa)^2 e^{(ik_1 – \kappa)a} – (ik_1 – \kappa)^2 e^{(ik_1 + \kappa)a} \right] $$

各項を展開します。
$$(ik_1 + \kappa)^2 = -k_1^2 + 2ik_1\kappa + \kappa^2$$
$$(ik_1 – \kappa)^2 = -k_1^2 – 2ik_1\kappa + \kappa^2$$

これを(27)式に代入します。
$$ 2A = \frac{F}{2ik_1\kappa} \left[ (-k_1^2 + 2ik_1\kappa + \kappa^2) e^{ik_1 a} e^{-\kappa a} – (-k_1^2 – 2ik_1\kappa + \kappa^2) e^{ik_1 a} e^{\kappa a} \right] $$
$$ 2A = \frac{F e^{ik_1 a}}{2ik_1\kappa} \left[ (-k_1^2 + \kappa^2)e^{-\kappa a} + 2ik_1\kappa e^{-\kappa a} – (-k_1^2 + \kappa^2)e^{\kappa a} – (-2ik_1\kappa)e^{\kappa a} \right] $$
$$ 2A = \frac{F e^{ik_1 a}}{2ik_1\kappa} \left[ (-k_1^2 + \kappa^2)(e^{-\kappa a} – e^{\kappa a}) + 2ik_1\kappa(e^{-\kappa a} + e^{\kappa a}) \right] $$
$$ 2A = \frac{F e^{ik_1 a}}{2ik_1\kappa} \left[ -(k_1^2 – \kappa^2)(e^{-\kappa a} – e^{\kappa a}) + 2ik_1\kappa(e^{-\kappa a} + e^{\kappa a}) \right] $$
$$ 2A = \frac{F e^{ik_1 a}}{2ik_1\kappa} \left[ (k_1^2 – \kappa^2)(e^{\kappa a} – e^{-\kappa a}) + 2ik_1\kappa(e^{\kappa a} + e^{-\kappa a}) \right] $$

ここで、双曲線関数 $\sinh x = \frac{e^x – e^{-x}}{2}$ および $\cosh x = \frac{e^x + e^{-x}}{2}$ を用いると、
$e^{\kappa a} – e^{-\kappa a} = 2\sinh(\kappa a)$
$e^{\kappa a} + e^{-\kappa a} = 2\cosh(\kappa a)$

$$ 2A = \frac{F e^{ik_1 a}}{2ik_1\kappa} \left[ (k_1^2 – \kappa^2) (2\sinh(\kappa a)) + 2ik_1\kappa (2\cosh(\kappa a)) \right] $$
$$ 2A = \frac{F e^{ik_1 a}}{ik_1\kappa} \left[ (k_1^2 – \kappa^2) \sinh(\kappa a) + 2ik_1\kappa \cosh(\kappa a) \right] $$
両辺を $2$ で割って整理すると、
$$ A = F e^{ik_1 a} \left[ \frac{k_1^2 – \kappa^2}{2ik_1\kappa} \sinh(\kappa a) + \frac{2ik_1\kappa}{2ik_1\kappa} \cosh(\kappa a) \right] $$
$$ A = F e^{ik_1 a} \left[ \frac{k_1^2 – \kappa^2}{2ik_1\kappa} \sinh(\kappa a) + \cosh(\kappa a) \right] $$
虚数単位 $i$ を分母から出すために、分子に $i$ を掛けます。
$$ A = F e^{ik_1 a} \left[ \cosh(\kappa a) – i \frac{k_1^2 – \kappa^2}{2 k_1 \kappa} \sinh(\kappa a) \right] $$
となります。ようやく、 $A$ と $F$ の関係式ができましたので、これを用いて透過率$T$を算出します。

\begin{aligned}T&=\frac{|F^{2}|}{|A^{2}|} \\ &=\dfrac{1}{ \cosh^{2}(\kappa a) + \left \lbrace\dfrac{k_1^2 – \kappa^2}{2 k_1 \kappa} \sinh(\kappa a) \right \rbrace^{2} } \\ &=\dfrac{4k_1^{2} \kappa^{2}}{4k_1^{2} \kappa^{2}\cosh^{2}(\kappa a) +(k_1^2 – \kappa^2)^{2}\sinh^{2}(\kappa a)} \end{aligned}

$\cosh^{2}+\sinh^{2}=1$より

\begin{aligned}T=\dfrac{4k_1^{2} \kappa^{2}}{4k_1^{2} \kappa^{2} +(k_1^2 + \kappa^2)^{2}\sinh^{2}(\kappa a)} \end{aligned}

Tは非零であることから、ポテンシャル障壁を透過する粒子が存在することが計算的にも分かりました。

※2乗する理由は、1乗の状態では波動関数だからです。そのままでは物理的意味を持ちません。2乗することで、初めて確率密度を表し、この比を取ることで透過率になるわけですね。

なお、反射率$R$についても、$R+T=1$から

\begin{aligned}R=\dfrac{(k_1^2 + \kappa^2)^{2}\sinh^{2}(\kappa a)}{4k_1^{2} \kappa^{2} +(k_1^2 + \kappa^2)^{2}\sinh^{2}(\kappa a)} \end{aligned}

※問題の誘導によっては、入射波の振幅$A$と反射波の振幅$B$の振幅の2乗の比を取り求める場合もあります。そもそも、反射率と透過率の和は1である事実を高知として扱っても良いのか議論もありますが、試験問題の分量を見ながら判断しましょう。

$E>V_{o}$の場合

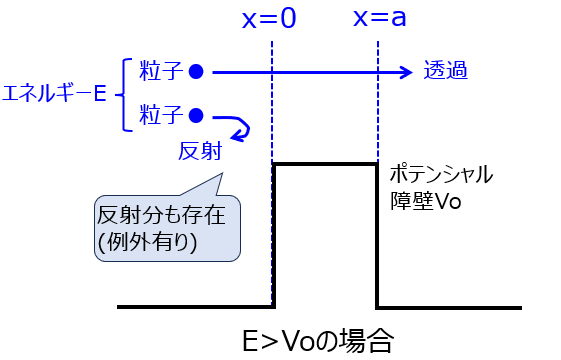
大小関係が逆転しますので、(5)式の$\kappa$が虚数になります。($i \kappa $) よって、(41)式、(42)式の双曲線関数が三角関数になるため

\begin{cases}T=\dfrac{4k_1^{2} \kappa^{2}}{4k_1^{2} \kappa^{2}\cos^{2}(\kappa a) +(k_1^2 – \kappa^2)^{2}\sin^{2}(\kappa a)} \\ R=\dfrac{(k_1^2 + \kappa^2)^{2}\sin^{2}(\kappa a)}{4k_1^{2} \kappa^{2} +(k_1^2 + \kappa^2)^{2}\sin^{2}(\kappa a)}\end{cases}

になります。粒子のエネルギーがポテンシャル障壁より大きいからと言って、全て透過するわけでもなく、反射成分も存在することが分かりました。

ただし、例外として、$ \kappa a=n \pi$ (nは自然数)のとき、反射率0、透過率1になります。これも試験でよく出てきます。