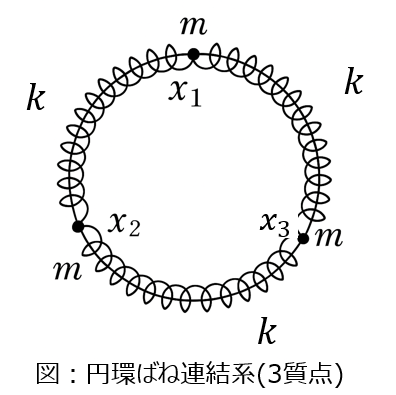
問:質量\(m\)の3個の質点をばね定数\(k\)のばねを用いて円環上に連結する。質点1,2,3の位置を\(x_{1},x_{2},x_{3}\)とするときの基準角振動数\(\omega_{1},\omega_{2},\omega_{3}\)を求めよ。
はじめに
ばねの連結系の振動は大学受験だけでなく、院試でもよく出てきます。京大の先端数理専攻で出題されたことがあります。振動の式\(Ae^{i \omega t}\)を仮定して運動方程式を解くことに変わりないですが、本記事では解析力学の知識を用いて解くことにします。
解析力学では、ニュートンの運動方程式に代わり、ラグランジュの運動方程式を用います。
ラグランジュの運動方程式
ラグランジアン\(L\)を用いて下記で表される。
\begin{aligned}\dfrac{d}{dt}\left(\dfrac{\partial L}{\partial \dot{x_{i}}}\right)-\dfrac{\partial L}{\partial \dot{x_{i}}}=0\end{aligned}
ただし、運動エネルギー\(T\)、ポテンシャルエネルギーを\(U\)とし\(L=T-U\)である。
また、\(x_{i}\)は各質点\(i=1,2,3\)それぞれの位置である。
本問の場合は、ばねのつり合いを考えています。
よって、運動エネルギー\(T\)は\(T=\frac{1}{2}m\ddot{x_{i}}\)、ポテンシャルエネルギー\(U\)は、\(U=\frac{1}{2}k(x_{i}^{2}-x_{i+1}^{2}\)で表されます。
これを(1)式に代入し、振動の式を仮定して微分方程式を\(\omega\)について解くことになります。実際に下記で試してみましょう。
解答例
問:3質点系の基準角振動数
まず、系の運動エネルギー、ポテンシャルエネルギーは
\begin{cases}T=\dfrac{1}{2}m(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}) \\ U=\dfrac{1}{2}k \left \lbrace(x_{1}-x_{2})^{2} + (x_{2}-x_{3})^{2}+(x_{1}-x_{3})^{2}\right \rbrace\end{cases}
これをラグランジュの運動方程式(1)式に代入すると
\begin{cases}m \ddot{x_{1}}+k(2x_{1}-x_{2}-x_{3})=0 \\ m \ddot{x_{2}}+k(-x_{1}+2x_{2}-x_{3})=0 \\ m \ddot{x_{3}}+k(x_{1}-x_{2}+2x_{3})=0\end{cases}
\(\lambda=\frac{k}{m}\)と置くと
\begin{cases}\ddot{x_{1}}+\lambda (2x_{1}-x_{2}-x_{3})=0 \\ \ddot{x_{2}}+\lambda (-x_{1}+2x_{2}-x_{3})=0 \\ \ddot{x_{3}}+\lambda (-x_{1}-x_{2}+2x_{3})=0\end{cases}
解\(x_{i}=A_{i}e^{i \omega t}\)を仮定し、上式に代入すると
\begin{cases}(\omega^{2}-2 \lambda)A_{1}+\lambda A_{2}+\lambda A_{3}=0 \\ \lambda A_{1}+(\omega^{2}-2 \lambda)A_{2}+\lambda A_{3}=0 \\ \lambda A_{1}+\lambda A_{2} +(\omega^{2}-2 \lambda)A_{3}=0\end{cases}
\(A_{1}=A_{2}=A_{3}\)以外の解が存在するとき、上式の行列式は0になるので
\begin{aligned}\begin{vmatrix}\omega^{2}-2\lambda & \lambda & \lambda \\ \lambda & \omega^{2}-2\lambda & \lambda \\ \lambda & \lambda & \omega^{2}-2\lambda\end{vmatrix}=0\end{aligned}
行基本変形、列基本変形をし、行列式を簡単に計算する。第1式に第2式、第3式を足し、第2式、第3式に対しても同じことをすると
\begin{aligned}(与式)&=\begin{vmatrix}\omega^{2} & \lambda & \lambda \\ \omega^{2} & \omega^{2}-2 \lambda & \lambda \\ \omega^{2} & \lambda & \omega^{2}-2 \lambda \end{vmatrix} \\ &= \begin{vmatrix}\omega^{2} & \lambda & \lambda \\ 0 & \omega^{2}-3 \lambda & 0 \\ 0 & 0 & \omega^{2}-3 \lambda \end{vmatrix}\end{aligned}
これを解くことで、基準角振動数は
\begin{aligned}\omega^{2}(\omega^{2}-3 \lambda)^{2}=0\end{aligned}
\begin{cases}\omega_{1}=0 \\ \omega_{2}=\omega_{3}=\sqrt{\dfrac{3k}{m}}\end{cases}
最後に
本記事では3個の質点の場合を考えましたが、n個になった場合もやることは同じです。行列の成分の数が増えますが、同じ行基本変形を行うことで基準角振動数を求められます。