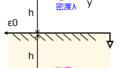
下記のように、点Aと点Bに電荷-q,+qが帯電している電気双極子について考える。点Aと点Bの間の長さを\(2l\)、中点をOとし、下記の問いに答えよ。
(1)中点Oから長さr離れた地点に点Pを設定する。線分ABおよび線分OPのなす角を\(\theta\)とし、点Pにおける電位を求めよ。
(2)\(r >> l\)のとき、点Pの電位と電場を求めよ。
(3)与えられた電気双極子から発生する電場の概形を書け。また、点Aの電荷も+qだった場合の概形もどうなるか説明せよ。
電気双極子とは
問題文で与えた図のように、正電荷と負電荷が近距離で置かれた電荷対のことを言います。
電気双極子の応用例
代表例として、下記2項目あります。
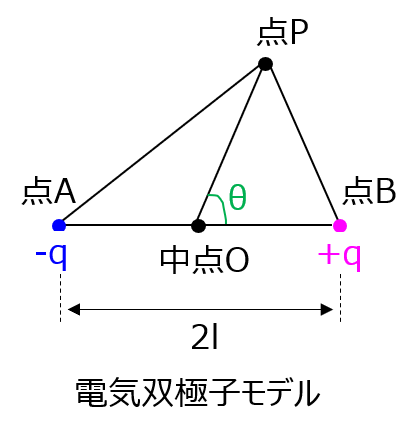
誘電体
誘電体に外部から電場をかけた時、分極電荷が発生します。
分極電荷は、正負の電荷対から構成されており、電気双極子と似ています。分極によって発生した単位体積当たりの双極子モーメントを分極ベクトルと言います。
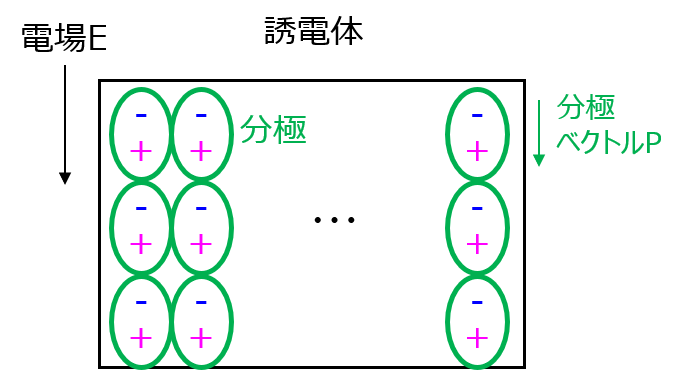
ダイポールアンテナ
ダイポールアンテナから発生する電場の計算を行う際、よく用います。
ダイポールアンテナの構成は、下記のようになっています。原点に長さ\(l\)のアンテナが置かれており、一方の端部では負電荷が帯電。もう一方では正電荷が帯電しています。
ここから発生する電場を求める時、導体の微小部分ごとに帯電している微小電荷のメッシュを切り、積分していく必要がありますが、非常に複雑な計算になります。
この課題を解決するため、電気双極子の概念が登場します。巨視的にアンテナを見れば、トータルして電荷的には中性であることに注目します。
問題を解くうえでの事前知識
電気双極子から発生する電場を見るために、高校物理でも登場した下記の電位の式を用います。
\begin{aligned}\phi=\dfrac{q}{4 \pi \varepsilon r}\end{aligned}
ただし、\(r\)は、点電荷から目標点までの距離です。
式(1)をrについて微分することで、電場を求めることができ、詳しい特性が分かるようになります。
例)空間電荷から発生する電気双極子の特性
下記の系を考えます。電荷が連続的に分布しているため、点Pでの電場は

\begin{aligned}\phi=\dfrac{1}{4 \pi \varepsilon_{o}}\int_{V}\dfrac{\rho(\boldsymbol{r’})}{|\boldsymbol{r}-\boldsymbol{r’}|}dV’\end{aligned}
\begin{aligned}\dfrac{1}{|\boldsymbol{r}-\boldsymbol{r’}|}&=\dfrac{1}{\sqrt{r^{2}+r’^{2}-2rr’\cos\theta}} \\ &=\dfrac{1}{r}\dfrac{1}{\sqrt{r+\frac{r’}{r}-2r’\cos\theta}}\end{aligned}
\(\dfrac{l^{2}}{r^{2}} \fallingdotseq 0, (1-x)^{-\frac{1}{2}}\fallingdotseq 1+\dfrac{x}{2}\)と近似できるので
\begin{aligned}\dfrac{1}{r}\dfrac{1}{\sqrt{r+\left(\frac{r’}{r}\right)^{2}-2r’\cos\theta}}&\fallingdotseq \dfrac{1}{r}\left(1+\dfrac{r’}{r}\cos\theta\right) \\ &= \dfrac{1}{r}+\dfrac{\boldsymbol{r}・\boldsymbol{r’}}{r^{3}}\end{aligned}
電荷分布の偏り(双極子モーメント)を\(\boldsymbol{p}\)とすると
\begin{aligned}\boldsymbol{p}=\int_{V}\boldsymbol{r’}\rho(\boldsymbol{r’})dV’\end{aligned}
(4)(5)式を(2)式に代入することで
\begin{aligned}\phi=\dfrac{Q}{4 \pi \varepsilon_{o} r}+\dfrac{\boldsymbol{p}・\boldsymbol{r}}{r^{3}}\end{aligned}
ただし、\(Q\)は空間電荷内の全電荷量である。
電気双極子を考える前提上、電荷の偏りはあるものの、全体としては0である。\(Q=0\)
これより、電気双極子から遠方における点の電位は下記のように示される。
\begin{aligned}\phi=\dfrac{\boldsymbol{p}・\boldsymbol{r}}{4 \pi \varepsilon_{o} r^{3}}\end{aligned}
あとは、これを微分することで電場\(\boldsymbol{E}\)を求めることができます。
\begin{aligned}\boldsymbol{E}&=-grad\left(\dfrac{\boldsymbol{p}・\boldsymbol{r}}{4 \pi \varepsilon_{o} r^{3}}\right) \\ &=\dfrac{1}{4 \pi \varepsilon_{o}}\left( \dfrac{3(\boldsymbol{p}・\boldsymbol{r})\boldsymbol{r}}{r^{5}}-\dfrac{\boldsymbol{p}}{r^{3}}\right) \end{aligned}
この考えを用いることで、点電荷の場合の電場分布も計算することが出来ます。(下記)
解答例(点電荷から発生する電気双極子)
(1)点Pにおける電位
余弦定理より、線分AP、線分BPの長さを求める。
\begin{aligned}\boldsymbol{AP}&=\sqrt{l^{2}+r^{2}-2lr\cos(\pi-\theta)} \\ &=\sqrt{l^{2}+r^{2}+2lr\cos(\theta)}\end{aligned}
\begin{aligned}\boldsymbol{BP}=\sqrt{l^{2}+r^{2}-2lr\cos(\theta)}\end{aligned}
この2つの電荷から発生する電位は、両者の電荷分を足せばよく
\begin{aligned}\phi&=\dfrac{-q}{4 \pi \varepsilon |\boldsymbol{AP}|}+\dfrac{q}{4 \pi \varepsilon |\boldsymbol{BP}|} \\ &=\dfrac{q}{4 \pi \varepsilon}\left(\dfrac{-1}{4 \pi \varepsilon \sqrt{l^{2}+r^{2}+2lr\cos(\theta)}} +\dfrac{1}{4 \pi \varepsilon \sqrt{l^{2}+r^{2}-2lr\cos(\theta)}}\right)\end{aligned}
(2)点Pにおける電位、電場(近似)
(4)式を変形し、近似できる形にする。
\begin{aligned}\phi &=\dfrac{q}{4 \pi \varepsilon r} \left(-\left(\dfrac{l^{2}}{r^{2}}+1+\dfrac{2l}{r}\cos \theta\right)^{-\frac{1}{2}}+\left(\dfrac{l^{2}}{r^{2}}+1-\dfrac{2l}{r}\cos \theta\right)^{-\frac{1}{2}}\right)\end{aligned}
例題と同じ近似を実施することにより
\begin{aligned}\phi&\fallingdotseq \dfrac{q}{4 \pi \varepsilon r}\left( -\left(1-\dfrac{l}{r}\cos\theta+1+\dfrac{l}{r}\cos\theta\right) \right) \\ \\ &= \dfrac{q}{4 \pi \varepsilon r} \dfrac{2l}{r}\cos\theta \end{aligned}
電場について、
\begin{aligned}\boldsymbol{E} &= -grad\phi \\ &=\left(-\dfrac{\partial \phi}{\partial r},\dfrac{\partial \phi}{r\partial \theta}\right) \\ &= \left( \dfrac{ql\cos\theta}{\pi \varepsilon r^{3}}, \dfrac{ql \sin\theta}{2 \pi \varepsilon r^{3}}\right)\end{aligned}
(3)電場の概形
(i)正負の電荷が正対している場合、(ii)正同士の電荷が正対している場合、2通りを考えます。
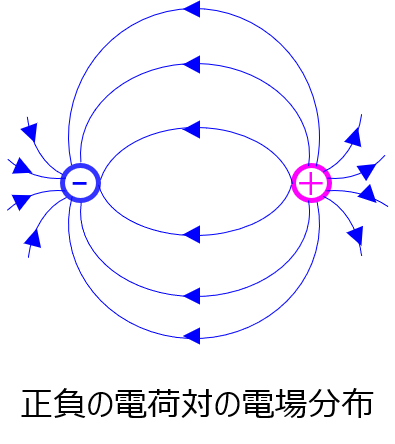
正負の電荷対から発生する電場
正の電荷から発生した電場は負の電荷へ引き寄せられます。(引力)
このため、下記のような電場分布となります。
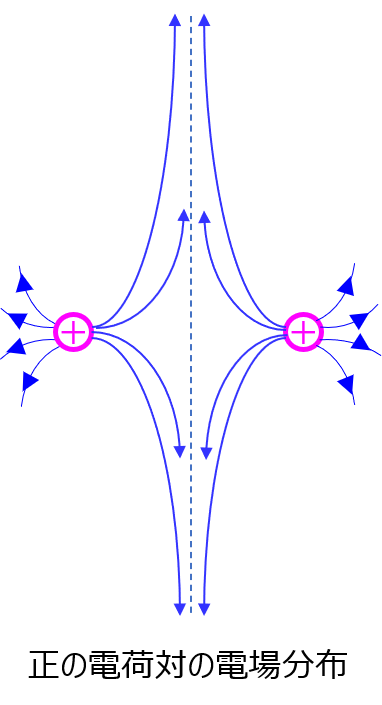
正同士の電荷対から発生する電場
斥力が働くので、一方の電荷から発生した電場は、もう一方の領域へ入ることが無いです。
中点で無限遠へ発散しますので、下記のような電場分布となります。
磁気双極子の場合
ベクトルポテンシャルを用い、同様の計算を行うことで(8)式と類似の形
\begin{aligned}\boldsymbol{B}=\dfrac{\mu_{o}}{4 \pi}\left( \dfrac{3(\boldsymbol{m}・\boldsymbol{r})\boldsymbol{r}}{r^{5}}-\dfrac{\boldsymbol{m}}{r^{3}}\right) \end{aligned}
を得られます。\((\varepsilon_{o}→\frac{1}{\mu},\boldsymbol{p}→\boldsymbol{m},\boldsymbol{E}→\boldsymbol{B})\)に置き換えています。
ここで、\(\boldsymbol{m}\)は磁気モーメントを表します。
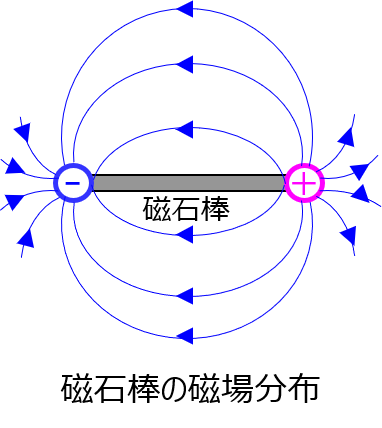
磁気双極子から発生する磁場
磁石は、電荷とは異なり、正のみ、負のみと独立で存在することができません。必ず正負の対として存在します。
このため、正負に存在する電気双極子から発生する電場と類似の概形で描けます。
最後に
電気双極子は理学部の院試で出やすいですが、たまに工学部の院試でも出題されます。最近では阪大で出題されましたので、同大学を出願する方は対策すると良いです。