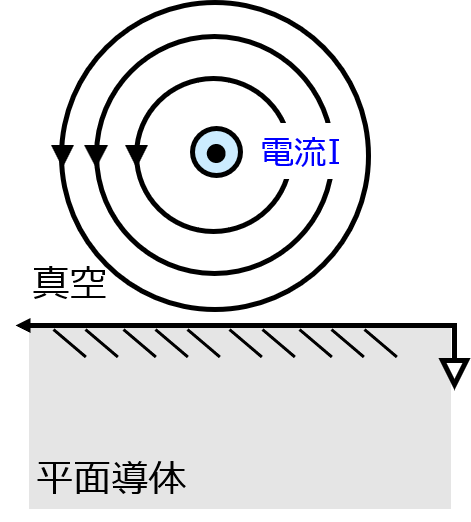
下記のように、真空中で無限遠に延びる円筒導体の紙面から飛び出す方向に電流を流す。円筒導体の下部には接地された無限平面導体が存在する。この時、下記の場合の磁力線の分布を図示せよ。
(1)導体の導電率\(\sigma\)が∞の場合(完全導体)
(2)導体の透磁率\(\mu\)が∞の場合(強磁性体)
完全導体の性質
問題文より、導電率が無限大の物質を言います。理想的な物質であるため、下記のような振る舞いをします。
電気的性質
抵抗率が0であるため、完全導体内部には電圧が発生しない=電場も発生しないです。ここで、境界面における電場の接線成分の連続性について考えます。真空中の電場を\(\boldsymbol{E_{1}}\)、完全導体中の電場を\(\boldsymbol{E_{2}}=0\)とすると
\begin{aligned}\boldsymbol{E_{1}}・\boldsymbol{t} =\boldsymbol{E_{2}}・\boldsymbol{t} \\ \boldsymbol{E_{1}}・\boldsymbol{t} = 0\end{aligned}
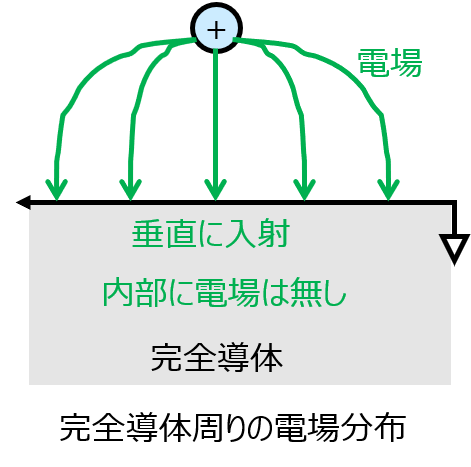
となり、真空中の電場の接線成分は0となります。よって、完全導体の表面に垂直に電場が入射します。
以上をまとめると、下図のようになります。
磁気的性質
次に、磁気的性質について考える。電磁誘導の法則の微分表現
\begin{aligned}rot\boldsymbol{E}=-\dfrac{\partial \boldsymbol{B}}{\partial t}\end{aligned}
について、電流が減衰しない状況下では変動磁場が発生しないので
\begin{aligned}rot\boldsymbol{E}=-\dfrac{\partial \boldsymbol{B}}{\partial t}=0\end{aligned}
が成立する。よって、完全導体中の任意の時間での磁束密度は
\begin{aligned}\boldsymbol{B}(t)=\boldsymbol{B}(0)\end{aligned}
になります。よって、完全導体になった瞬間にかかっている磁束密度をそのまま保持します。
補足:超電導体との違い
上記のように、完全導体では時間次第で内部に磁場が入り込みますが、超電導体に関しては常に内部の磁場が\(\boldsymbol{B}=0\)になります。
これをマイスナー効果と言います。このとき
\begin{aligned}\boldsymbol{B}=\mu_{o}(\boldsymbol{H}+\boldsymbol{M})=0\end{aligned}
が成立し、\(\boldsymbol{M}=-\boldsymbol{H}\)が導かれます。
この時の磁気感受率は\(\chi_{m}=-1\)となります。これを、完全反磁性と言います。
強磁性体の性質
問題文より、透磁率が無限大の物質を言います。
磁気的性質
完全導体のときと同じように、異なる媒質間の境界条件を考えます。
真空中の磁場を\(\boldsymbol{H_{1}}\)、強磁性体内部の磁場を\(\boldsymbol{H_{2}}\)とすると
\begin{aligned}\boldsymbol{H_{2}}=\dfrac{\boldsymbol{B_{2}}}{\mu}=0\end{aligned}
だから、境界条件の式は以下のようになります。
\begin{aligned}\boldsymbol{H_{1}}・\boldsymbol{t} =\boldsymbol{H_{2}}・\boldsymbol{t} \\ \boldsymbol{H_{1}}・\boldsymbol{t}=0 \end{aligned}
真空中の磁場の接線成分は0になります。強磁性体には垂直に磁場が入射します。
解答例
(1)完全導体中の磁力線
(4)式より、完全導体になった時点での磁場をそのまま保持します。よって、下記の2通り考えられます。
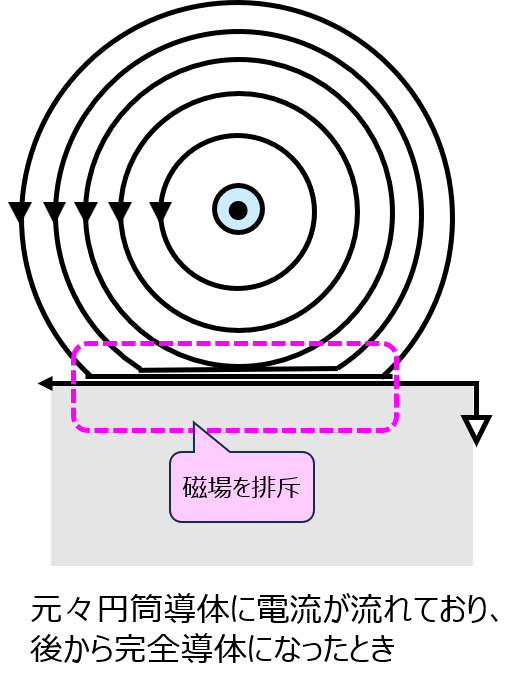
- 元々円筒導体に電流が流れており、平面坂が後から完全導体になったとき
- 完全導体が既に存在しており、後から円筒導体1に電流を流した場合
1.の場合
円筒導体に電流を流した時の磁力線をそのまま保存します。よって、境界面で磁場を排斥するようなことは無く、アンペールの法則で求めた磁場分布が媒質によらず適用されます。
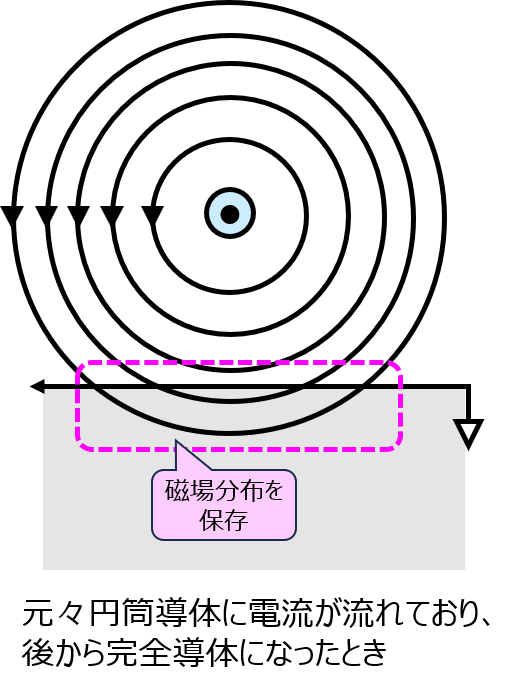
2.の場合
円筒導体内に存在する磁場は元々0だったため、後から磁力線が印加されても排斥します。よって、下記のような分布になります。
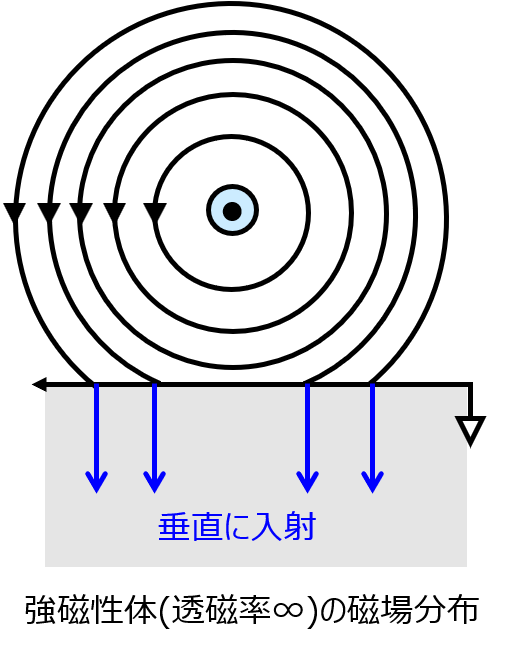
(2)強磁性体中の磁力線(透磁率∞)
強磁性体の性質で述べたように、磁場の接線成分は0になり、垂直成分だけ残ります。よって、下記のような分布になります。
最後に
導電率∞の物体は”完全導体”という専用の名前があります。一方で、透磁率∞の磁性体には、専用の名前があるかどうかを管理人は知りません。強磁性体の名前で代用しましたが、用語的には∞の領域でなくとも適用できてしまいます。
もし、専用の名前をご存じの方がいらっしゃる場合はご教授頂けると助かります。