下記3つの場合の点P(0,0,a)における電場を求めよ。
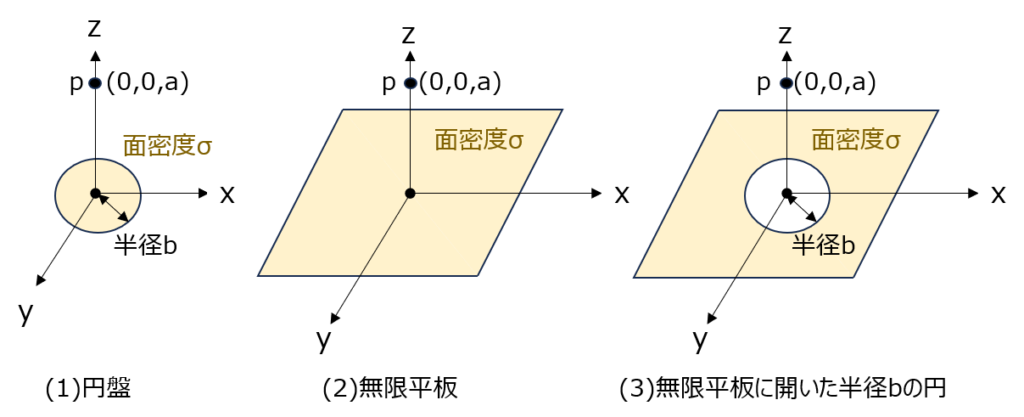
(1)半径bで、面密度\(\sigma\)で帯電した円盤
(2)面密度\(\sigma\)で帯電した無限平板
(3)面密度\(\sigma\)で帯電した無限平板のうち、半径bの円盤部分のみ穴が開いた板
クーロンの法則とは
電荷同士にかかる力の量を示す関係式を言います。距離\(r\)離れた点電荷\(q_{1},q_{2}\)に対してかかる力は下記になります。
\begin{aligned}F=\dfrac{q_{1}q_{2}}{4 \pi \varepsilon_{o} r^{2}}\end{aligned}
また、\(F=q_{2}E\)より、点電荷\(q_{1}\)から\(r\)の地点で発生する電場は下記になります。
\begin{aligned}E=\dfrac{q_{1}}{4 \pi \varepsilon_{o} r^{2}}\end{aligned}
なお、点電荷のような離散的な物体でなくとも、\(\sigma dS\)なる連続した電荷密度を持つ物体から一部を切り出した場合でも上式は成立します。(\(q_{1}\)を\(\sigma dS\)に置き換える。)
本記事では、点電荷では無く連続した物体でも、積分をすることによって物体全体から発生する電場を求められることを示していきます。
解答例
方針
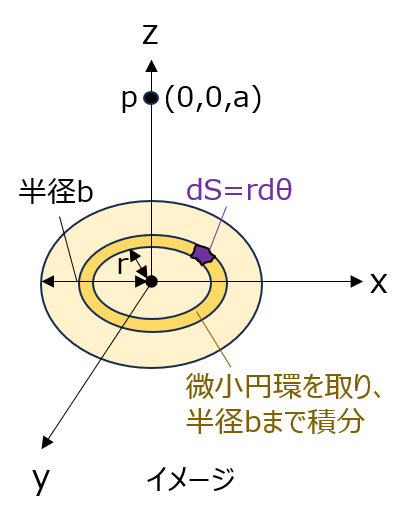
まず、微小区間\(dS=rd\theta dr\)を取り、下記の手順で積分します。
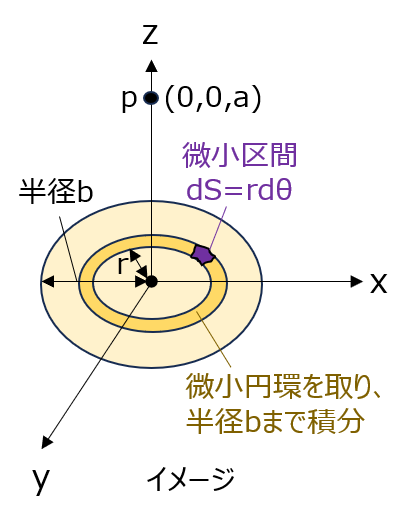
- \(\theta [0, 2 \pi]\)で積分し、幅drの薄い円盤から発生する電場を考える。
- \(dr [0,b]\)で積分し、円盤全体で発生する電場を求める。
微小区間\(dS=rd\theta dr\)の状態で発生する電場は、z成分だけでなく、xy成分も持っています。このため、成分分解して積分を考え始めると大変になります。
そこで、\(\theta\)を最初に[0,2π]分、一周積分します。こうすると、円盤上の対角地点同士でxy成分の電場を打ち消し合い、z成分のみ考えれば良くなります。
(2)については、b⇒∞の極限を考えることにより、結果を求められます。
(3)については、(2)の結果に対し(1)の結果を引き算すれば求まります。理由は後述します。
(1)半径bの円盤から発生する電場
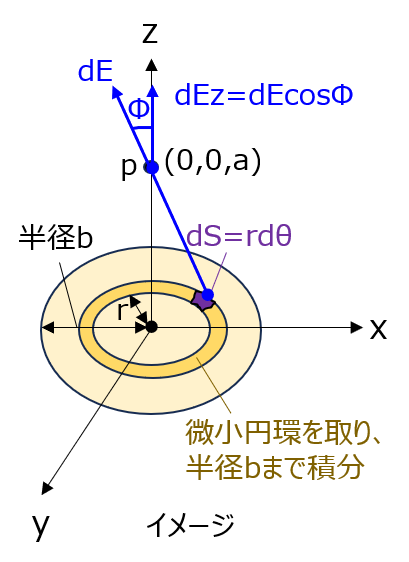
\(dS=rd\theta dr\)から点Pに発生する電場のz成分は、クーロンの法則により
\begin{aligned}dE_{z}=\dfrac{\sigma r dr d\theta}{4 \pi \varepsilon_{o}(r^{2}+a^{2})}\cos \phi\end{aligned}
\(\cos \phi=\dfrac{a}{\sqrt{r^{2}+a^{2}}}\)だから、上式は
\begin{aligned}dE_{z}=\dfrac{\sigma r dr d\theta}{4 \pi \varepsilon_{o}(r^{2}+a^{2})^{3/2}}\end{aligned}
これを区間[0,2π]で積分し、半径r、幅drの微小円環から発生する電場は
\begin{aligned}E_{z}&=\dfrac{\sigma r dr d\theta}{4 \pi \varepsilon_{o}(r^{2}+a^{2})^{3/2}} \\ &=\dfrac{\sigma a}{4 \pi \varepsilon_{o}}\int^{2 \pi}_{0}\dfrac{rdr d\theta}{(r^{2}+a^{2})^{3/2}} \\ &= \dfrac{\sigma a}{2 \varepsilon_{o}}\dfrac{rdr}{(r^{2}+a^{2})^{3/2}} \end{aligned}
最後に、rを[0,b]の区間で積分することで、求める電場は
\begin{aligned}E_{total1}&=\int^{b}_{0}\dfrac{\sigma a}{2 \varepsilon_{o}}\dfrac{rdr}{(r^{2}+a^{2})^{3/2}} \\ &=-\dfrac{\sigma a}{2 \varepsilon_{o}}\left \lbrack \dfrac{1}{\sqrt{r^{2}+a^{2}}} \right \rbrack ^{b}_{0} \\ &=\dfrac{\sigma a}{2 \varepsilon_{o}}\left(\dfrac{1}{a}-\dfrac{1}{\sqrt{a^{2}+b^{2}}} \right )\end{aligned}
(2)無限平板から発生する電場
(1)の答えより、b⇒∞の極限を考えれば良いので
\begin{aligned}E_{total2}=\dfrac{\sigma}{2 \varepsilon_{o}}\end{aligned}
電界はxy平面に対し垂直で、大きさは高さz=aに依らないことが分かりました。
別解
ガウスの法則を用いることでも解くことが出来ます。
xy平面の断面積がS、高さが2aの直方体を原点を中心として取る。
xy平面のみ電場が鎖交するため、下記のように式変形ができる。
\begin{aligned}\int_{S} \boldsymbol{E}・d\boldsymbol{S}&=\int_{上面}\boldsymbol{E_{total2}}・d\boldsymbol{S}+\int_{下面}\boldsymbol{E_{total2}}・d\boldsymbol{S} \\ &=2E_{total2}S=\dfrac{\sigma S}{\varepsilon_{o}}\end{aligned}
これを解いて
\begin{aligned}E_{total2}=\dfrac{\sigma}{2 \varepsilon_{o}}\end{aligned}
(3)円盤状の穴が開いた無限平板から発生する電場
これは類題経験が無いと難しいと思います。重ね合わせの原理より、下記の系で発生する電場を足し合わせます。
- 面電荷密度\(\sigma\)の無限平板から発生する電場\(E_{1}\)
- 面電荷密度\(-\sigma\)の半径bの円盤から発生する電場\(E_{2}\)
円盤部分の電荷が打ち消し合うため、与えられた系と同等の状態になります。
\(E_{1}\)は(2)の結果(7式)。\(E_{2}\)は(1)の結果(6式)の符号を逆転すれば良いので、求める電場は
\begin{aligned}E_{total3}&=E_{total2}-E_{total1} \\ &=\dfrac{\sigma a}{2 \varepsilon_{o} \sqrt{a^{2}+b^{2}}}\end{aligned}